递归之汉诺塔

汉诺塔

算法描述

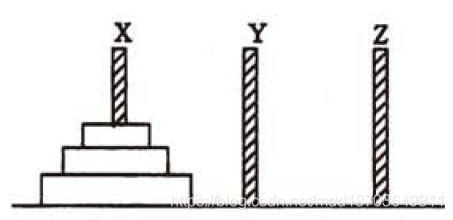
假设有3个命名为X，Y和Z的塔座，在塔座X上插有n个直径大小各不相同、依小到大编号为1,2，…，n的圆盘。现要求将X轴上的n个圆盘移至塔座Z上并仍按同样顺序叠排，圆盘移动时必须遵循下列规则：

1. 每次只能移动一个圆盘
2. 圆盘可以插在X，Y和Z中的任一塔座上
3. 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上

请问怎么移动？

代码描述

/**
         * 汉诺塔(唯有递归才能解决的问题):
         *
         * ABC三个柱子
         * 
         * 1.3个盘片在A柱子(上到下是小盘到大盘)
         * 
         * 2.要求把盘片移动到C柱子
         * 
         * 3.移动过程中,柱子不能出现小盘在下面
         *
         * 4.需求:请列出移动的过程,还有移动的次数;
         *
         * 先分析大过程,忽视细节
         * 
         * 1. A柱子的3个盘子,两个盘子肯定借助C移动到B,完成一个大阶段:
         * 
         * 2. 当A柱子的只剩下最大盘子,那么移动到C
         * 
         * 3. B柱子的两个盘借助A移动到C
         * 
         * 解决的关键是记住大的方向
         */
        public class Demo01 {

            private static int moveCount;

            public static void main(String[] args) {
                getNum(2);
            }

            private static void getNum(int num) {
                char a = 'A';
                char b = 'B';
                char c = 'C';
                moveCount = 0;//计数器
                move(num, a, b, c);
                System.out.println("moveCount = "+moveCount);//打印移动的步骤
            }

            /**
             *
             * @param moveNum
             *            移动的个数
             * @param a
             *            原柱子
             * @param b
             *            辅助柱
             * @param c
             *            目标柱子
             */
            private static void move(int moveNum, char a, char b, char c) {//原->辅助->目标
                moveCount++;
                // 看图:2.只有一个时,A把("第"n)个移动到C
                // 内部: 只有一个时,原柱子->目标柱子
                if (moveNum == 1) {
                    System.out.println("from # " + a + " move " + moveNum + " to " + c);
                } else {
                    // 看图: 1.A借C把("共"n-1个)移动到B
                    // 内部: 多个:原柱子->辅助柱子
                    // C变成辅助,所以排在第二位,B变成目标;
                    move(moveNum - 1, a, c, b);
                    System.out.println("from - " + a + " move " + moveNum + " to " + c);
                    // 看图: 3.B借A把("共"n-1)个移动到C
                    // 内部: 多个:辅助柱->目标柱子
                    // A是辅助,所以排在第二位置,C变目标;
                    move(moveNum - 1, b, a, c);
                }
            }
        }