In image processing, computer vision and related fields, an image moment is a certain particular weighted average (moment) of the image pixels' intensities, or a function of such moments, usually chosen to have some attractive property or interpretation.
Image moments are useful to describe objects after segmentation. Simple properties of the image which are found via image moments include area (or total intensity), its centroid, and information about its orientation.
Contents
[hide]
Raw moments[edit]
For a 2D continuous function f(x,y) the moment (sometimes called "raw moment") of order (p + q) is defined as
for p,q = 0,1,2,... Adapting this to scalar (greyscale) image with pixel intensities I(x,y), raw image moments Mij are calculated by
In some cases, this may be calculated by considering the image as a probability density function, i.e., by dividing the above by
A uniqueness theorem (Hu [1962]) states that if f(x,y) is piecewise continuous and has nonzero values only in a finite part of the xy plane, moments of all orders exist, and the moment sequence (Mpq) is uniquely determined by f(x,y). Conversely, (Mpq) uniquely determines f(x,y). In practice, the image is summarized with functions of a few lower order moments.
Examples[edit]
Simple image properties derived via raw moments include:
- Area (for binary images) or sum of grey level (for greytone images): M00
- Centroid: { x, y } = {M10/M00, M01/M00 }
Central moments[edit]
Central moments are defined as
where  and
and  are the components of the centroid.
are the components of the centroid.
If ƒ(x, y) is a digital image, then the previous equation becomes
The central moments of order up to 3 are:
It can be shown that:
Central moments are translational invariant.
Examples[edit]
Information about image orientation can be derived by first using the second order central moments to construct a covariance matrix.
The covariance matrix of the image 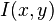 is now
is now
-
![\operatorname{cov}[I(x,y)] = \begin{bmatrix} \mu'_{20} & \mu'_{11} \\ \mu'_{11} & \mu'_{02} \end{bmatrix}](http://upload.wikimedia.org/math/1/5/7/157055506512ae54596eba0b98019101.png) .
.
The eigenvectors of this matrix correspond to the major and minor axes of the image intensity, so the orientation can thus be extracted from the angle of the eigenvector associated with the largest eigenvalue. It can be shown that this angle Θ is given by the following formula:
The above formula holds as long as:
The eigenvalues of the covariance matrix can easily be shown to be
and are proportional to the squared length of the eigenvector axes. The relative difference in magnitude of the eigenvalues are thus an indication of the eccentricity of the image, or how elongated it is. The eccentricity is
Scale invariant moments[edit]
Moments ηi j where i + j ≥ 2 can be constructed to be invariant to both translation and changes in scale by dividing the corresponding central moment by the properly scaled (00)th moment, using the following formula.
Rotation invariant moments[edit]
It is possible to calculate moments which are invariant under translation, changes in scale, and also rotation. Most frequently used are the Hu set of invariant moments:[1][2]

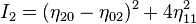


![I_5 = (\eta_{30} - 3\eta_{12}) (\eta_{30} + \eta_{12})[ (\eta_{30} + \eta_{12})^2 - 3 (\eta_{21} + \eta_{03})^2] + (3 \eta_{21} - \eta_{03}) (\eta_{21} + \eta_{03})[ 3(\eta_{30} + \eta_{12})^2 - (\eta_{21} + \eta_{03})^2]](http://upload.wikimedia.org/math/e/f/1/ef1d0cf39c26181f68b017d10ee46079.png)
![I_6 = (\eta_{20} - \eta_{02})[(\eta_{30} + \eta_{12})^2 - (\eta_{21} + \eta_{03})^2] + 4\eta_{11}(\eta_{30} + \eta_{12})(\eta_{21} + \eta_{03})](http://upload.wikimedia.org/math/8/3/b/83b7598760be3446a28043104db166bd.png)
![I_7 = (3 \eta_{21} - \eta_{03})(\eta_{30} + \eta_{12})[(\eta_{30} + \eta_{12})^2 - 3(\eta_{21} + \eta_{03})^2] - (\eta_{30} - 3\eta_{12})(\eta_{21} + \eta_{03})[3(\eta_{30} + \eta_{12})^2 - (\eta_{21} + \eta_{03})^2].](http://upload.wikimedia.org/math/9/2/4/924523044350520cd06bbab880796dc0.png)
The first one, I1, is analogous to the moment of inertia around the image's centroid, where the pixels' intensities are analogous to physical density. The last one, I7, is skew invariant, which enables it to distinguish mirror images of otherwise identical images.
A general theory on deriving complete and independent sets of rotation invariant moments was proposed by J. Flusser[3] and T. Suk.[4] They showed that the traditional Hu's invariant set is not independent nor complete. I3 is not very useful as it is dependent on the others. In the original Hu's set there is a missing third order independent moment invariant:
External links[edit]
- Analysis of Binary Images, University of Edinburgh
- Statistical Moments, University of Edinburgh
- Variant moments, Machine Perception and Computer Vision page (Matlab and Python source code)
- Hu Moments introductory video on YouTube
References[edit]
- Jump up^ M. K. Hu, "Visual Pattern Recognition by Moment Invariants", IRE Trans. Info. Theory, vol. IT-8, pp.179–187, 1962
- Jump up^ http://docs.opencv.org/modules/imgproc/doc/structural_analysis_and_shape_descriptors.html?highlight=cvmatchshapes#humoments Hu Moments' OpenCV method
- Jump up^ J. Flusser: "On the Independence of Rotation Moment Invariants", Pattern Recognition, vol. 33, pp. 1405–1410, 2000.
- Jump up^ J. Flusser and T. Suk, "Rotation Moment Invariants for Recognition of Symmetric Objects", IEEE Trans. Image Proc., vol. 15, pp. 3784–3790, 2006.





 本文探讨了图像处理和计算机视觉领域中影像矩的概念及其应用,包括原始矩、中心矩、尺度不变矩、旋转不变矩等,并介绍了如何通过影像矩来描述物体、提取属性,如面积、重心、方向等。此外,文章还讨论了影像矩在不同场景下的应用,如图像区域的大小、形状、位置和旋转角度的确定。
本文探讨了图像处理和计算机视觉领域中影像矩的概念及其应用,包括原始矩、中心矩、尺度不变矩、旋转不变矩等,并介绍了如何通过影像矩来描述物体、提取属性,如面积、重心、方向等。此外,文章还讨论了影像矩在不同场景下的应用,如图像区域的大小、形状、位置和旋转角度的确定。





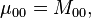






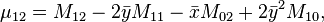
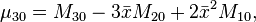


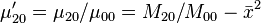







![I_8 = \eta_{11}[ ( \eta_{30} + \eta_{12})^2 - (\eta_{03} + \eta_{21})^2 ] - (\eta_{20}-\eta_{02}) (\eta_{30}+\eta_{12}) (\eta_{03}+\eta_{21})](http://upload.wikimedia.org/math/f/e/2/fe2c908ee5039b2329fb25e179a32b7e.png)
















 1010
1010

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








