大二数据结构课程设计-从数据流获取中位数-这是四个曲折的分析历程

于 2021-01-13 20:12:27 发布
阅读量482 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： 数据结构与算法 文章标签： 数据结构 链表 c++ 二叉树 树堆
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/mazamu/article/details/112581753

文章目录

题目及要求

随时找到数据流中的中位数
[问题描述]
随时找到数据流中的中位数：有一个源源不断地吐出整数的数据流，假设你有足够的空间来保存吐出的数。请设计一个名叫MedianHolder的结构，MedianHolder可以随时取得之前吐出所有数的中位数。
[基本要求]
（1）如果MedianHolder已经保存了吐出的N个数，那么任意时刻将一个新数加入到MedianHolder的过程，其时间复杂度是O(logN)。
（2）取得已经吐出的N个数整体的中位数的过程，时间复杂度为O(1)。
原来这是leetcode上的一道题目

题目大意：给定一段无限多的数据，需要你尽快插入，并且立马得出中位数

只想看最终分析结果的可以 索引 飞到分析四和代码，分析一的代码不用理会。

运行结果

奇数情况：
奇数情况
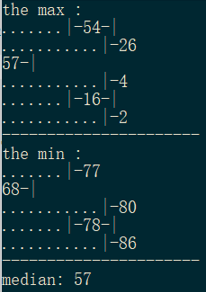
偶数情况
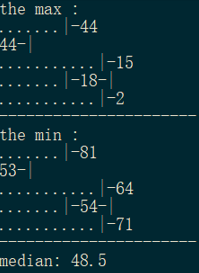
在这里插入图片描述
先偶数，后插入一个数变成奇数的情况：
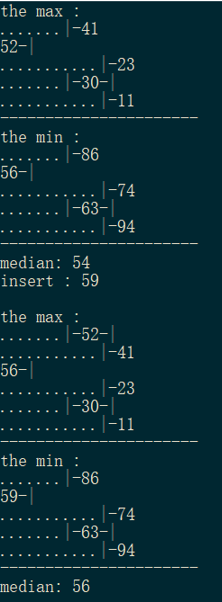
在这里插入图片描述

分析过程

分析一

刚开始看到第一个要求要实现O（logN）的插入时间复杂度，便想到用二分，想到二分就想到二叉树，第一次实现便是用二叉树，后来又想了想二叉树的极端情况下会成链表，那时候插入就不是O（logN）了。便很自然再想到AVL树（但是有坑）。
实现AVL树的过程比较复杂，这里遇到的困难是旋转的方向，一共有四种情况，有两种比较复杂（分别是左右型和右左型），分别是要先左旋再右旋和先右旋再左旋。
实现了AVL树，在内存足够的情况下，再用一个可扩容的Vector来存下中序遍历过的数据，重载[ ]运算符，根据总数/2来查找中位数，分清奇偶的情况就可以了，限于篇幅，想要查看AVL旋转和平衡的实现的可以点击右边链接查看 AVL的实现代码

后来又重写了一个，因为用AVL和vector并没有确切地实现题目要求。
原因：数据流是随时流动的，每次进入一个数 都可以求出已经流出的数（包括此刻的这个）的中位数。而我实现的只是求出 已经流出来的数据 的中位数，而增加数据的话在AVL树上插入且时间复杂度O（logN）是没问题的，但是得到中位数却要 重新存一遍（时间复杂度O（n）） 或者 插入 Vector里（如果在这个数据结构里实现一次二分插入或是其它O（logN）排序算法 ），但是这样的话用AVL树的意义何在？ 。

错了重头再来：

分析二

这时碰到的问题是找中位数，我便打算只用链表存，但是只用链表的话，无法实现二分。网上搜了一下，发现有种数据结构叫做跳转表。看别人说，跳转表在redis和levelDB上被用的比较频繁，但无奈没实现过，也尝试去理解了，按伪代码去写了一些，但是二分是有了，但是找中位数，emmmm，就我感觉那个跳转表的随机生成函数，要找到中位数还是得要O（logN）。因为有人说跳转表实现可以用中位数来索引，但是我不会。而且真要做出来拿这个去答辩，说实在的，也没啥信心。

分析三

便又回到AVL树那里，我为什么会想到AVL树是因为之前有看过课程实现过一次AVL树，课程里还讲到一个Treap的数据结构，Treap的意思是 Tree+heap，Treap里有两个值<first,second>，它是先根据first进行二叉排列，然后根据second用AVL旋转来调整树使得 Treap 既是树又是堆（比如说最大堆）。
这时候已经有一点正确的想法了，就是把数据流分为两部分，前一部分是最大堆，后一部分是最小堆，然后中位数就是 最大堆的最大值（奇数）或者 最大堆最大值和最小堆的最小值/2（偶数）。
便突发奇想，在AVL树上魔改，数据流送进一个数据a，那我根据这个数据再随机生成数据b，不就有<a,b>了吗。。。。。我真的天真。
然后改代码把自己改懵了（具体过程省略，反正你们都懂的（手动狗头））。

分析四（最终）

逃不过现实，还是回到最淳朴的来实现（为菜鸡的自己而悲伤）。
决定好用两个堆，前面是大顶堆，后面是小顶堆。
设定：
大顶堆的所有元素都小于小顶堆的所有元素。
奇数情况：大顶堆包含中位数和前半段数据，小顶堆包含后半段数据。
偶数情况：大顶堆包含前半段数据，小顶堆包含后半段数据。
综上：大顶堆的数据的个数 等于 （（小顶堆的数据的个数）或者（小顶堆的数据的个数+1））。
那么接下来需要考虑插入数据时该怎么办：
如果已经流出的数据总数为偶数，如果下一个要插入的数据大于小顶堆的堆顶，显然这个数出现在后半段数据中，但是直接插入到小顶堆里不符合我们的设定，（大顶堆的数据总是大于等于小顶堆数据），则先插入小顶堆，再把小顶堆的堆顶弹出，把小顶堆的堆顶插入大顶堆里。
如果已经流出的数据总数为奇数，下一个流出的数据应该放到小顶堆里。但是需要判断它的值，如果它的值小于大顶堆的堆顶，则先把它插进大顶堆里，然后弹出大顶堆的堆顶，把大顶堆的堆顶插入小顶堆里。

随机数流的数据结构（半个结果）

//MedianHolder.h
#include"heap.cpp"
class MedianHolder{
public:
	MedianHolder() {
		max = new heap(1);
		min = new heap(0);
	}
	void insert(int num){
		if (min->size() != max->size()){//节点数不等,则max的节点数比min的节点数多1
			if (num < max->top()){ //保持max的最大值小于 min的最小值
				max->push(num);
				num = max->top();
				max->pop();
			}
			min->push(num);
		}
		else{//节点数相等
			if (min->size() && num > min->top()){
				min->push(num);
				num = min->top();
				min->pop();
			}
			max->push(num);
		}
	}
	double getMedian() {
		if (min->size() != max->size()) return max->top();
		else return 1.0 * (max->top() + min->top()) / 2;
	}
	void Print(){
		cout<<"the max : "<<endl;
		max->Print();
		cout<<"the min : "<<endl;
		min->Print();
	}
private:
    heap *max;
    heap *min;
};

如果你很熟悉vector的话（把上面的heap改成vector），调用关于堆的函数，上面这段代码简简单单就可以完成，下面的完全不用看。

链式heap的数据结构

heap.h

//heap.h
#include<iostream>
#include<deque>
#include<stack>
#include<queue>
#include<time.h>
using namespace std;
struct pnode{
	int data;
	pnode* left,* right,* father;
	pnode(int e){ data=e; left = right = father = NULL; }
 
};
 
struct father{
public:
	father(){ lrson = -1; point = NULL;}
	int lrson;
	pnode* point;
};
 
class heap{
public:
	heap(){ head = NULL;type = 0; sizes = 0;}
    heap(int x) {head = NULL;type = x; sizes = 0;}
    ~heap(){}
	void push(int e);
	int pop();
    int size(){return sizes;}
	int top(){if(!head) return -1;return head->data;}
	bool empty();
	void swap(int &a,int &b);
    //调整堆
	void fix(pnode* p){
        if(type == 0) fix0(p);
        else fix1(p);
	}
    void fix0(pnode* p);//小顶堆修正
    void fix1(pnode* p);//大顶堆修正

	//查看堆建立的是否正确
    void show();
    void Print() {
		int level = 1;
		Print(head,level);
        cout<<"----------------------"<<endl;
	}
    void Print(pnode* root,int level);


    int type; //0是小顶堆，1是大堆顶

private:
    deque<father>nodeAdd;//找到要插入的位置
	stack<pnode*>delStack;//找到要删除的位置
	pnode* head;
    int sizes;
};

heap.cpp

//heap.cpp
#include"heap.h"
bool heap::empty(){
	return head == NULL;
}

void heap::swap(int &a,int &b) {
    int t = a;
    a = b;
    b = t;
}

void heap::push(int e){
    this->sizes++;
	pnode* temSon = NULL;
	if(!head){//根节点为空
		pnode* tem = new pnode(e);
		head = tem;
		father fat;
		fat.point = tem;
		fat.lrson = 1;
		nodeAdd.push_back(fat);
		fat.lrson=2;
		nodeAdd.push_back(fat);
		delStack.push(tem);
		return;

	}else{//根节点非空
		father temFat = nodeAdd.front();
		nodeAdd.pop_front();

		temSon = new pnode(e);
		temSon->father = temFat.point;

		delStack.push(temSon);

		if(temFat.lrson == 1){//插入左节点
			temFat.point->left=temSon;
			father fat;
			fat.point = temSon;
			fat.lrson = 1;
			nodeAdd.push_back(fat);
			fat.lrson=2;
			nodeAdd.push_back(fat);
		}else{//插入右节点
			temFat.point->right = temSon;
			father fat;
			fat.point = temSon;
			fat.lrson = 1;
			nodeAdd.push_back(fat);
			fat.lrson = 2;
			nodeAdd.push_back(fat);
		}
	}
    if(type == 0){//小顶堆
        while(temSon->father){ //向上交换
            if(temSon->data < temSon->father->data){
                swap(temSon->father->data,temSon->data);
                temSon=temSon->father;
            }
            else
                return;
        }
    }else {//大顶堆
        while(temSon->father){//向上交换
            if(temSon->data > temSon->father->data ){
                swap(temSon->father->data,temSon->data);
                temSon=temSon->father;
            }
            else
                return;
        }        
    }
}
int heap::pop(){
    if(empty()) return 0; 
    this->sizes--;
	int temData = head->data;
	pnode* sonNode = delStack.top();//要删除的节点位置
	delStack.pop();
	if(sonNode->father == NULL){//根节点
		head = NULL;
		while(!nodeAdd.empty())
			nodeAdd.pop_back();
		while(!delStack.empty())
			delStack.pop();
		return 1;
	}

	if(sonNode->father->left == sonNode) {//要删除的节点在左孩子
		father fat;
		fat.point = sonNode->father;
		fat.lrson = 1;
		nodeAdd.push_front(fat);//如果是左孩子，则如果插入则会插入右孩子
		nodeAdd.pop_back();
		nodeAdd.pop_back();
		sonNode->father->left = NULL;
	}else {//要删除的节点在右孩子
		father fat;
		fat.point = sonNode->father;
		fat.lrson = 2;
		nodeAdd.push_front(fat);
		nodeAdd.pop_back();
		nodeAdd.pop_back();
		sonNode->father->right = NULL;
	}

	head->data = sonNode->data;
	delete sonNode;
	sonNode = NULL;
	fix(head);

	return 1;
}

void heap::Print(pnode* root,int level) {
    if(!root) return;
    Print(root->right,level+1);
    if(level > 1) {
        for(int i = 0; i < 4*level-1; i++) cout<<'.';
        if(!root->left && !root->right) cout<<"|-"<<root->data<<endl;
        else cout<<"|-"<<root->data<<"-|"<<endl;
    }else {
        cout<<root->data<<"-|"<<endl;
    }
    Print(root->left,level+1);   
}

void heap::show(){
    cout<<"输出\n";
    queue<pnode*>pp;
    pnode* tem;
    pp.push(head);
    while(!pp.empty())
    {
        tem=pp.front();
        pp.pop();
        cout<<tem->data<<"  ";
        if(tem->left)
            pp.push(tem->left);
        if(tem->right)
            pp.push(tem->right);
    }
        cout<<"\n\n";
}
void heap::fix0(pnode* p){
    if(p->left == NULL)
        return;
    if(p->right){//左右节点同时存在
        if(p->right->data >= p->left->data && 
        p->left->data < p->data){//左节点比右节点小或等于的情况
            swap(p->left->data,p->data);
            fix(p->left);
        }
        else if(p->right->data <= p->left->data &&
        p->right->data < p->data){//右节点比左节点小或等于的情况
            swap(p->right->data,p->data);
            fix(p->right);
        }
    }
    else{//无右节点情况
        if(p->left->data >= p->data){
            return;
        }
        else{
            swap(p->left->data,p->data);
            fix(p->left);
        }

    }
}

void heap::fix1(pnode* p){
    if(p->left==NULL)
        return;
    if(p->right){//左右节点同时存在
        if(p->right->data <= p->left->data && 
        p->left->data > p->data){//左节点比右节点小或等于的情况
            swap(p->left->data,p->data);
            fix(p->left);
        }
        else if(p->right->data >= p->left->data &&
        p->right->data > p->data){//右节点比左节点小或等于的情况
            swap(p->right->data,p->data);
            fix(p->right);
        }
    }
    else{//无右节点情况
        if(p->left->data <= p->data){
            return;
        }
        else{
            swap(p->left->data,p->data);
            fix(p->left);
        }

    }
}

不要问为什么要用链式heap？问就是另一个悲伤的故事了。

text.cpp

//text.cpp
#include"MedianHolder.h"
#include<stdlib.h>
#include<time.h>
int main() 
{ 
    srand((unsigned)time(NULL)); 
    MedianHolder * t = new MedianHolder;
    int a;int i = 0;
    for(i = 0; i < 10; i++) {
        a = (rand()%100);
        t->insert(a);
    }
    t->Print();
    cout<<"median: "<<t->getMedian()<<endl;
    int num;
    while(1) {
        cout<<"insert : ";
        if(num == -1) break;
        cin>>num;
        t->insert(num);
        cout<<endl;
        t->Print();
        cout<<"median: "<<t->getMedian()<<endl;
    }    
    return 0;
}

总结

数据结构课程设计题目有八道，我有把八道都做一遍的想法，但是。。
emmmmm，有时间就都搞一下，听说有几道是研究生面试题目。
怎么说，别的没有，抗压能力明显提高，上一年碰到问题会烦操且会有种抗拒心理（怎么又出错了呢），今年只想到冲冲冲，可能这就是编程给我带来的某些改变，或者说习惯了改改改。。。。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值