LeetCode 669. Trim a Binary Search Tree（修剪二叉搜索树）

最新推荐文章于 2025-05-26 02:30:00 发布

原创最新推荐文章于 2025-05-26 02:30:00 发布 · 256 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#Trim a Binary Search Tree #修剪二叉搜索树

LeetCode 专栏收录该内容

50 篇文章

订阅专栏

本文介绍了LeetCode 669题目的解决方法，重点在于理解如何通过递归调整二叉搜索树中节点的引用关系，以达到修剪目的。当节点值不在指定范围内时，分别向左右子树查找，找到范围内节点并返回其引用，从而实现修剪。

题目：
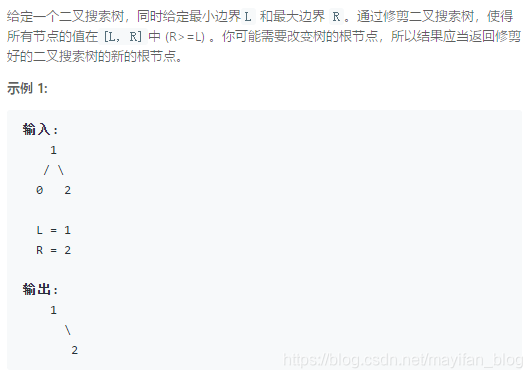
在这里插入图片描述
如何去看待修剪这个说法：
修剪即去掉那些不在范围内的节点，那么我们是不是可以理解为调整节点之间的引用关系，把这个“修剪”的过程和递归联系起来。
调整引用关系的思路：
递归的节点不满足条件的情况：这是类似于递归查找的部分，如果当前root的值不满足条件，那么就会放弃这个节点的值，若它小于L，就去当前节点的右节点去找，如果它大于R，就去当前节点的左节点去找。当找到一个在范围内的节点，是会通过这个多级的引用传递返回过来的。

        if(root==null){
        	return null;
        }else if(root.val<L){
        	return trimBST(root.right, L, R);
        }else if(root.val>R){
        	return trimBST(root.left, L , R);
        }

递归节点满足条件的情况：这是递归代码的下一个部分，如果当前节点的值在范围内，那么就返回把当前节点做和之前的根节点一样的事情，然后返回当前节点的引用。

        root.left=trimBST(root.left, L , R);
        root.right=trimBST(root.right, L, R);
        return root;

完整代码：

      class TreeNode {
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode(int x) { val = x; }
}

class Solution {
    public TreeNode trimBST(TreeNode root, int L, int R) {
        if(root==null){
        	return null;
        }else if(root.val<L){
        	return trimBST(root.right, L, R);
        }else if(root.val>R){
        	return trimBST(root.left, L , R);
        }
        root.left=trimBST(root.left, L , R);
        root.right=trimBST(root.right, L, R);
        return root;
    }
}