文章介绍了由JianfuBai等人开发的ASinhCoshOptimizer，这是一种新式优化器，特别针对高维数据优化，具有全局搜索能力。文章详细描述了其原理和在不同领域的应用潜力，包括机器学习、信号处理和电力系统等。
✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，
代码获取、论文复现及科研仿真合作可私信。
🍎个人主页：Matlab科研工作室
🍊个人信条：格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
很高兴能够在这篇博客文章中向大家介绍一项新的技术：Jianfu Bai, Yifei Li, Mingpo Zheng, Samir Khatir, Brahim Benaisa, Laith Abualigah, Magd Abdel Wahab, A Sinh Cosh Optimizer，该技术将于2023年在《Knowledge-Based Systems》杂志上发表。
这项技术的研究人员来自多个国家和地区，他们在优化算法方面有着丰富的经验和知识。这项技术的核心是一种全新的优化器，名为“A Sinh Cosh Optimizer”。它的设计灵感来自于双曲正弦和余弦函数，这些函数在数学和物理学中都有广泛的应用。
优化器是机器学习中的重要组成部分，它可以帮助模型更快地收敛并提高准确性。然而，传统的优化器在处理高维数据时往往效果不佳，因为它们容易陷入局部最优解。而“A Sinh Cosh Optimizer”则可以更好地处理高维数据，并且能够更快地找到全局最优解。
这项技术的优点不仅仅在于它的高效性，还在于它的可扩展性。研究人员已经将该技术应用于多个不同的数据集和模型中，并且取得了非常好的效果。这表明该技术可以适用于各种不同的应用场景，并且可以帮助研究人员更快地开发出高效的机器学习模型。
总的来说，Jianfu Bai, Yifei Li, Mingpo Zheng, Samir Khatir, Brahim Benaisa, Laith Abualigah, Magd Abdel Wahab, A Sinh Cosh Optimizer是一项非常有前途的技术。它的出现将为机器学习领域带来新的发展机遇，并且可以帮助研究人员更好地解决实际问题。我们期待着看到更多的研究人员将这项技术应用于实际应用中，并且带来更多的创新和进步。
📣 部分代码
% Sinh Cosh Optimizer (SCHO)%% Developed in MATLAB R2022a%% programming: Jianfu Bai%% e-Mail: Jianfu.Bai@UGent.be, magd.abdelwahab@ugent.be% Soete Laboratory, Department of Electrical Energy, Metals, Mechanical Constructions, and Systems,% Faculty of Engineering and Architecture, Ghent University, Belgium%% paper: Jianfu Bai, Yifei Li, Mingpo Zheng, Samir Khatir, Brahim Benaisa, Laith Abualigah, Magd Abdel Wahab, A Sinh Cosh Optimizer, Knowledge-Based Systems (2023).% The detail information of 23 classical benchmark functions% lb is the lower bound% up is the uppper bound% dim is the number of variables (dimension)function [lb,ub,dim,fobj] = Get_Functions_details(F)switch Fcase 'F1'fobj = @F1;lb=-100;ub=100;dim=30;case 'F2'fobj = @F2;lb=-10;ub=10;dim=30;case 'F3'fobj = @F3;lb=-100;ub=100;dim=30;case 'F4'fobj = @F4;lb=-100;ub=100;dim=30;case 'F5'fobj = @F5;lb=-30;ub=30;dim=30;case 'F6'fobj = @F6;lb=-100;ub=100;dim=30;case 'F7'fobj = @F7;lb=-1.28;ub=1.28;dim=30;case 'F8'fobj = @F8;lb=-500;ub=500;dim=30;case 'F9'fobj = @F9;lb=-5.12;ub=5.12;dim=30;case 'F10'fobj = @F10;lb=-32;ub=32;dim=30;case 'F11'fobj = @F11;lb=-600;ub=600;dim=30;case 'F12'fobj = @F12;lb=-50;ub=50;dim=30;case 'F13'fobj = @F13;lb=-50;ub=50;dim=30;case 'F14'fobj = @F14;lb=-65.536;ub=65.536;dim=2;case 'F15'fobj = @F15;lb=-5;ub=5;dim=4;case 'F16'fobj = @F16;lb=-5;ub=5;dim=2;case 'F17'fobj = @F17;lb=[-5,0];ub=[10,15];dim=2;case 'F18'fobj = @F18;lb=-2;ub=2;dim=2;case 'F19'fobj = @F19;lb=0;ub=1;dim=3;case 'F20'fobj = @F20;lb=0;ub=1;dim=6;case 'F21'fobj = @F21;lb=0;ub=10;dim=4;case 'F22'fobj = @F22;lb=0;ub=10;dim=4;case 'F23'fobj = @F23;lb=0;ub=10;dim=4;endend% F1function o = F1(x)o=sum(x.^2);end% F2function o = F2(x)o=sum(abs(x))+prod(abs(x));end% F3function o = F3(x)dim=size(x,2);o=0;for i=1:dimo=o+sum(x(1:i))^2;endend% F4function o = F4(x)o=max(abs(x));end% F5function o = F5(x)dim=size(x,2);o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);end% F6function o = F6(x)o=sum(abs((x+.5)).^2);end% F7function o = F7(x)dim=size(x,2);o=sum([1:dim].*(x.^4))+rand;end% F8function o = F8(x)o=sum(-x.*sin(sqrt(abs(x))));end% F9function o = F9(x)dim=size(x,2);o=sum(x.^2-10*cos(2*pi.*x))+10*dim;end% F10function o = F10(x)dim=size(x,2);o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);end% F11function o = F11(x)dim=size(x,2);o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;end% F12function o = F12(x)dim=size(x,2);o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));end% F13function o = F13(x)dim=size(x,2);o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));end% F14function o = F14(x)aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];for j=1:25bS(j)=sum((x'-aS(:,j)).^6);endo=(1/500+sum(1./([1:25]+bS))).^(-1);end% F15function o = F15(x)aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);end% F16function o = F16(x)o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);end% F17function o = F17(x)o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;end% F18function o = F18(x)o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));end% F19function o = F19(x)aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];o=0;for i=1:4o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend% F20function o = F20(x)aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];cH=[1 1.2 3 3.2];pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;....2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];o=0;for i=1:4o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend% F21function o = F21(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:5o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend% F22function o = F22(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:7o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend% F23function o = F23(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];o=0;for i=1:10o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endendfunction o=Ufun(x,a,k,m)o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));end
⛳️ 运行结果
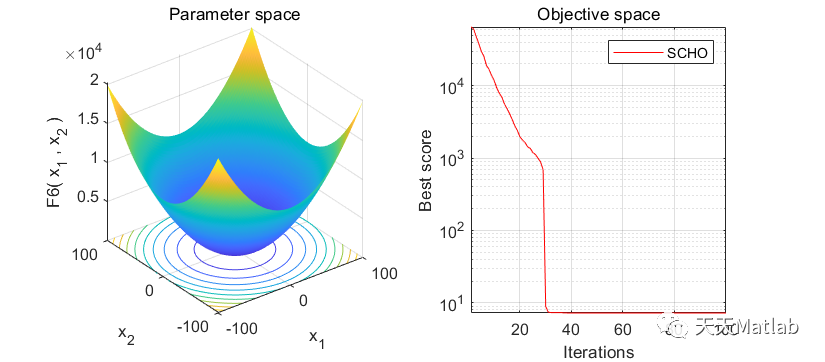
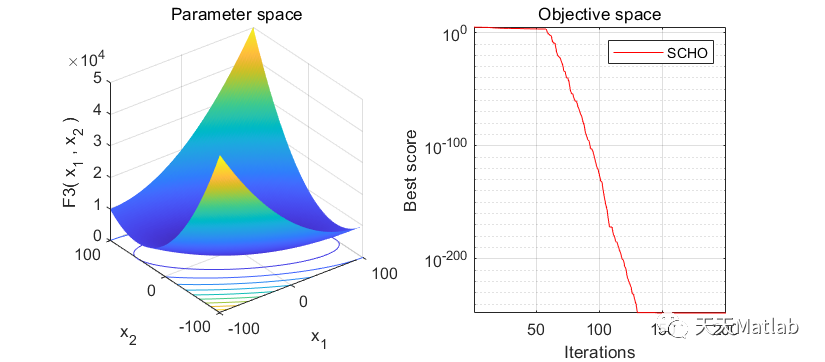
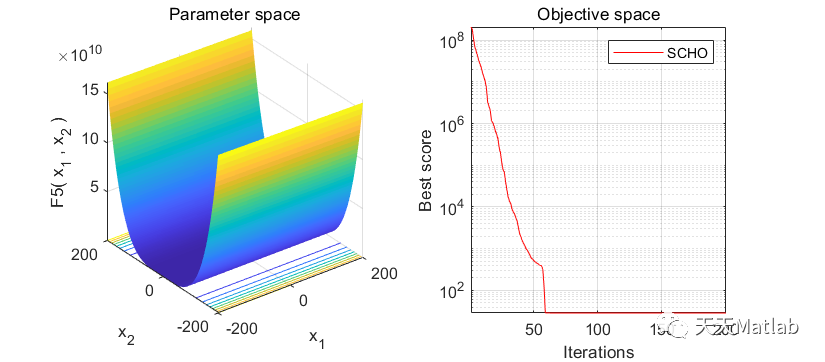
🔗 参考文献
Jianfu Bai, Yifei Li, Mingpo Zheng, Samir Khatir, Brahim Benaisa, Laith Abualigah, Magd Abdel Wahab, A Sinh Cosh Optimizer, Knowledge-Based Systems (2023).
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
