基于二进制粒子群算法（BPSO）的计算卸载策略求解matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

⛄ 内容介绍

基于移动边缘计算(MEC)环境下的计算卸载技术有效缓解了传统无线网络数据中心的处理压力,提升了系统服务质量.针对计算密集型任务卸载使得移动终端设备能量消耗大的问题,提出了一种基于二进制粒子群算法(BPSO)的计算卸载策略.

⛄ 完整代码

clc

clear

close all

% 初始化种群

narvs = 30;  %解的维数

n = 100;     %粒子的个数100个

x_ub = 10;    

x_lb = -10;   

vmax = 1.2;                  %粒子的最大速度

w = 0.9;                     % 惯性权重

c1 = 2;                      % 每个粒子的个体学习因子，也称为个体加速常数

c2 = 2;                      % 每个粒子的社会学习因子，也称为社会加速常数

%%初始种群

x = randsrc(n,narvs,[0,1;0.5,0.5]);      %设置0和1随机出现的概率均为0.5，x为n行narvs列的矩阵

v = -vmax + 2*vmax .* rand(n,narvs);     %v为n行narvs列的矩阵

s=0;

fitness=zeros(n,1);

for i=1:n

   

   for k=1:30

      f=((1-x(i,k))*10e-26*((rand(1)+1)*5*10^9)^3)+x(i,k)*(0.5*((rand(1)*2+1)/250000))+0.01*(((rand(1)+1)*5*10^9)/(rand(1)*4*10^9));

      s=s+f;

   end

   fit=s; 

   fitness(i,1)=fit;

end

fitness;                                 %计算种群初始值

pbest = x;                               % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）,局部最优解

ind = find(fitness == max(fitness), 1);  % 找到适应度最大的那个粒子的下标     find函数：返回fitness函数中前1个非零元素的位置

gbest = x(ind,:);                        % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量），全局最优解

K=100;                       %迭代次数

fitnessbest=zeros(K,1);      %保存每一代的函数值  ； zeros(K,1)生成一个K行1列的0矩阵

best=0;

bestOne =zeros(1,30);       %  zeros(1,30)生成一个1行10列的0矩阵

for t = 1:K                  %迭代循环100次  

    for i = 1:n

        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));

        % 判断速度是否超过限制了(还可以取模)

        for j = 1:narvs

            if v(i,j) < -vmax

                v(i,j) = -vmax;

                

            elseif v(i,j) > vmax

                v(i,j) = vmax;

            end

        end

        x

        v

        %sigmoid函数将例子的速度映射到0-1之间

        vs(i,:)=1./(1+exp(-v(i,:))); 

        for j = 1:narvs

            if rand < vs(i,j)

                x(i,j) = 1;

            else

                x(i,j) = 0;

            end

        end

       x

        s=0;

        for k=1:narvs

            f=((1-x(i,k))*10e-26*((rand(1)+1)*5*10^9)^3)+x(i,k)*(0.5*((rand(1)*2+1)/250000))+0.01*(((rand(1)+1)*5*10^9)/(rand(1)*4*10^9));

            s=s+f;

        end

        fit =s;

      

        s=0;

        for k=1:narvs

            f=((1-pbest(i,k))*10e-26*((rand(1)+1)*5*10^9)^3)+pbest(i,k)*(0.5*((rand(1)*2+1)/250000))+0.01*(((rand(1)+1)*5*10^9)/(rand(1)*4*10^9));

            s=s+f;

        end

        fpbest=s;

           

          s=0;

        for k=1:30

            f=((1-gbest(k))*10e-26*((rand(1)+1)*5*10^9)^3)+gbest(k)*(0.5*((rand(1)*2+1)/250000))+0.01*(((rand(1)+1)*5*10^9)/(rand(1)*4*10^9));

            s=s+f;

        end

        fgbest=s;

       

     % 重新计算第i个粒子的适应度

        if fit > fpbest                      % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度

            pbest(i,:) = x(i,:);                       % 那就更新第i个粒子迄今为止找到的最佳位置（更新局部最优解）

        end

        if  fit > fgbest                                % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度

            gbest = pbest(i,:);                        % 那就更新所有粒子迄今为止找到的最佳位置（更新全局最优解）

        end 

    end

    h = fgbest;

    if h>best         

        best = h; 

        best0ne = gbest;  

    end

    fitnessbest(t,1)=best; 

end

bestOne;

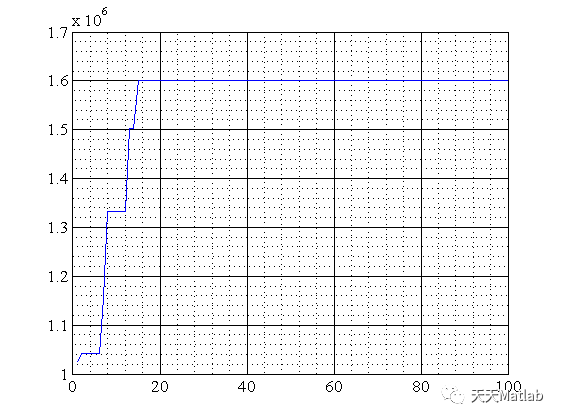
figure

plot(1:K,fitnessbest,'-');

grid on;

grid minor;

⛄ 运行结果

⛄ 参考文献

[1]姚玉海, 王增平, 郭昆亚,等. 基于E占优的多目标二进制粒子群算法求解配电网故障恢复[J]. 电力系统保护与控制, 2014, 42(23):6.

⛳️ 完整代码

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料