【Kelm分类】基于粒子群算法优化核极限学习机实现数据分类附matlab代码

1 简介

当今社会癌症的发病率越来越高,对人类健康构成严重的威胁,伴随着人类基因组计划(Human Genome Project)的发展,可以通过DNA微阵列技术产生大量的基因表达数据,但是数据集的样本一般都是维数高而且样本量比较少。如何从数据中挖掘出有用的信息和知识,对肿瘤的辅助诊断至关重要。极限学习机(Extreme Learning Machine,ELM)能够通过输入样本逼近复杂的非线性映射,在基因数据分类时学习速度快,并且能够避免陷入局部收敛的状况,但是在处理非线性数据时,分类结果较差,并且不稳定。为了得出精度更高且更稳定的基因分类算法,本文对ELM算法进行了研究。主要工作有:1)提出一种基于粒子群的核极限学习机算法。通过分析ELM算法的原理,结合其优缺点,引入了核函数,采用核极限学习机(Kernel Extreme Learning Machine,KELM)对给定数据进行初始化,产生一组输入权值和隐层偏置,针对KELM内权随机赋值导致算法不稳定的问题,用粒子群优化算法对内权参数进行优化,最终得到分类效果较优并且稳定的PSO-KELM分类器。

2 部分代码

function [zbest yy]=PSO_fun(c1,c2,D,maxgen,sizepop,Vmax,Vmin,popmax,popmin,randdata1,randdata2,model)​%% 产生初始粒子和速度for i=1:sizepop    %随机产生一个种群    pop(i,:)=randdata1(i,:);    %初始种群    V(i,:)=randdata2(i,:);  %初始化速度    %计算适应度    fitness(i)=fun(pop(i,:),model);   %粒子的适应值end​%% 个体极值和群体极值[bestfitness bestindex]=min(fitness);zbest=pop(bestindex,:);   %全局最佳gbest=pop;    %个体最佳fitnessgbest=fitness;   %个体最佳适应度值fitnesszbest=bestfitness;   %全局最佳适应度值​%% 迭代寻优for i=1:maxgen        for j=1:sizepop                %速度更新        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));        V(j,find(V(j,:)>Vmax))=Vmax;        V(j,find(V(j,:)<Vmin))=Vmin;                %种群更新        pop(j,:)=pop(j,:)+V(j,:);        pop(j,find(pop(j,:)>popmax))=popmax;        pop(j,find(pop(j,:)<popmin))=popmin;                %适应度值        fitness(j)=fun(pop(j,:),model);        end        for j=1:sizepop                %个体最优更新        if fitness(j) < fitnessgbest(j)            gbest(j,:) = pop(j,:);            fitnessgbest(j) = fitness(j);        end                %群体最优更新        if fitness(j) < fitnesszbest            zbest = pop(j,:);            fitnesszbest = fitness(j);        end    end     yy(i)=fitnesszbest;           end​​

3 仿真结果

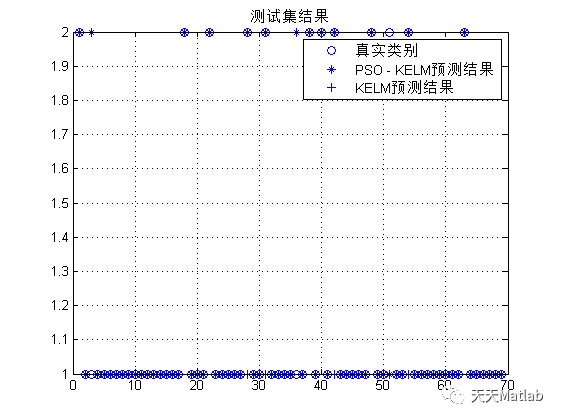
​4 参考文献

[1]杨勇. 基于粒子群优化策略的核极限学习机及其应用研究[D]. 兰州大学.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。