【鲸鱼算法】基于收敛因子非线性变化的鲸鱼优化算法(IWOA) 求解单目标优化问题附matlab代码

1 简介

针对基本鲸鱼优化算法在处理复杂全局优化问题时存在解精度低和收敛速度慢等缺点,提出一种收敛因子随进化迭代次数非线性变化的改进鲸鱼优化算法.该算法利用混沌方法替代随机方法初始化种群,使群体具有较好的多样性.受粒子群算法惯性权重启发,设计出一种随进化迭代次数增加而非线性变化的收敛因子更新公式,以平衡算法的全局搜索和局部搜索能力.对当前最优鲸鱼个体执行混沌扰动策略以扩大其搜索范围.选取6个高维标准测试函数进行数值实验,结果表明该算法具有较高的收敛精度和较快的收敛速度.

2 部分代码

%_________________________________________________________________________%% 鲸鱼优化算法             %%_________________________________________________________________________%% The Whale Optimization Algorithmfunction [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)​% initialize position vector and score for the leader Leader_pos=zeros(1,dim);Leader_score=inf; %change this to -inf for maximization problems​​%Initialize the positions of search agentsPositions=initialization(SearchAgents_no,dim,ub,lb);​Convergence_curve=zeros(1,Max_iter);​t=0;% Loop counter​% Main loopwhile t<Max_iter    for i=1:size(Positions,1)                % Return back the search agents that go beyond the boundaries of the search space        Flag4ub=Positions(i,:)>ub;        Flag4lb=Positions(i,:)<lb;        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;                % Calculate objective function for each search agent        fitness=fobj(Positions(i,:));                % Update the leader        if fitness<Leader_score % Change this to > for maximization problem            Leader_score=fitness; % Update alpha            Leader_pos=Positions(i,:);        end            end        a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)        % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)    a2=-1+t*((-1)/Max_iter);        % Update the Position of search agents     for i=1:size(Positions,1)        r1=rand(); % r1 is a random number in [0,1]        r2=rand(); % r2 is a random number in [0,1]                A=2*a*r1-a;  % Eq. (2.3) in the paper        C=2*r2;      % Eq. (2.4) in the paper                        b=1;               %  parameters in Eq. (2.5)        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)                p = rand();        % p in Eq. (2.6)                for j=1:size(Positions,2)                        if p<0.5                   if abs(A)>=1                    rand_leader_index = floor(SearchAgents_no*rand()+1);                    X_rand = Positions(rand_leader_index, :);                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)                                    elseif abs(A)<1                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)                end                            elseif p>=0.5                              distance2Leader=abs(Leader_pos(j)-Positions(i,j));                % Eq. (2.5)                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);                            end                    end    end    t=t+1;    Convergence_curve(t)=Leader_score;end

3 仿真结果

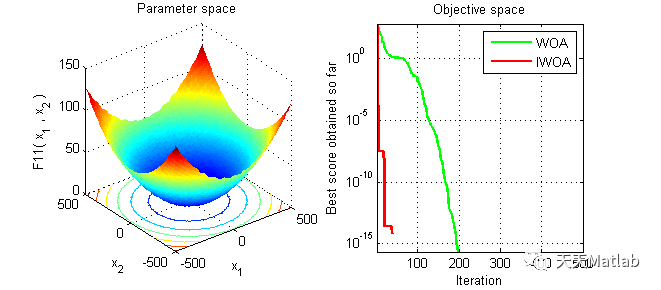
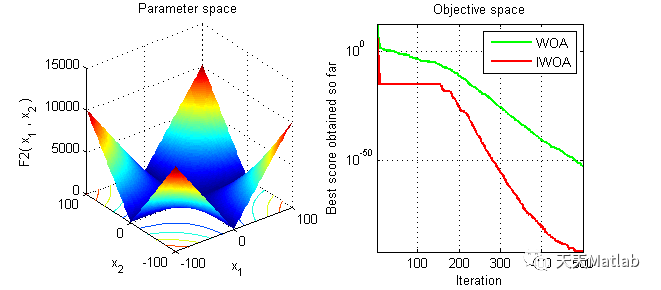
4 参考文献

[1]龙文, 伍铁斌, 唐斌. 收敛因子非线性变化的鲸鱼优化算法[J]. 兰州理工大学学报, 2017, 43(6):6.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。