一些模板和应用

kmp模板

 一、HDU1711 求第一个匹配子串起始位置

 

const

  maxn=1000000;

var

  t,n,m,i:longint;

  next,a,b:array[0..maxn]of longint;

procedure getnext;

var

  i,j:longint;

begin

  next[0]:=-1;

  i:=0;j:=-1;

  while i<m do

  begin

    if (j=-1)or(b[i+1]=b[j+1]) then

    begin

      inc(i);inc(j);next[i]:=j;

    end

    else j:=next[j];

  end;

end;

function kmp:longint;

var

  sum:longint;

  i,j:longint;

begin

  i:=0;j:=0;

  while (i<n) do

  begin

    if (j=-1)or(a[i+1]=b[j+1]) then

    begin

      inc(i);inc(j);

    end

    else j:=next[j];

    if (j=m) then exit(i-m+1);

  end;

  exit(-1);

end;

procedure init;

var

  i:longint;

begin

  readln(n,m);

  for i:=1 to n do

    read(a[i]);

  readln;

  for i:=1 to m do

    read(b[i]);

  getnext;

end;

begin

  readln(t);

  for i:=1 to t do

  begin

    init;

    writeln(kmp);

  end;

end.

 

二、HDU1686 求子串数量（可重叠）

 

const

  maxn=1000000;

var

  t,n,m,i:longint;

  next:array[0..maxn]of longint;

  a,b:ansistring;

procedure getnext;

var

  i,j:longint;

begin

  next[0]:=-1;

  i:=0;j:=-1;

  while i<m do

  begin

    if (j=-1)or(b[i+1]=b[j+1]) then

    begin

      inc(i);inc(j);next[i]:=j;

    end

    else j:=next[j];

  end;

end;

function kmp:longint;

var

  sum:longint;

  i,j:longint;

begin

  i:=0;j:=0;sum:=0;

  while (i<n) do

  begin

    if (j=-1)or(a[i+1]=b[j+1]) then

    begin

      inc(i);inc(j);

    end

    else j:=next[j];

    if (j=m) then

    begin

      inc(sum);

      j:=next[j];//统计数量，可重叠  j:=0 不可重叠

    end;

  end;

  exit(sum);

end;

procedure init;

var

  i:longint;

begin

  readln(b);

  readln(a);

  n:=length(a);m:=length(b);

  getnext;

end;

begin

  readln(t);

  for i:=1 to t do

  begin

    init;

    writeln(kmp);

  end;

end.

 

三、KMP求最小循环节

经典问题 : 给出一个由某个循环节构成的字符串，要你找出最小的循环节，例如 abababab 最小循环节当是 ab ，而类似 abab 也可以成为它的循环节，但并非最短。

 

分析 :

对于上述问题有两个结论 

如果对于next数组中的 i， 符合 i % ( i - next[i] ) == 0 && next[i] != 0 , 则说明字符串循环，而且

循环节长度为:    i - next[i]

循环次数为:       i / ( i - next[i] )

https://www.cnblogs.com/Rubbishes/p/7564992.html

 

LCA模板

 一、树上倍增求LCA

 

const

  maxn=40000;

var

  f:array[0..maxn,0..32]of longint;

  e:array[1..maxn*2,1..2]of longint;

  last,next:array[1..maxn*2]of longint;

  v:array[1..maxn]of boolean;

  lg,dis,dep:array[1..maxn]of longint;

  t,n,m,sum,i,j,x,y,z:longint;

procedure add(x,y,z:longint);

begin

  inc(sum);

  e[sum,1]:=y;e[sum,2]:=z;

  next[sum]:=last[x];

  last[x]:=sum;

end;

procedure dfs(x,y:longint);

var

  i:longint;

begin

  v[x]:=true;

  i:=last[x];dep[x]:=y;

  while i>0 do

  begin

    if v[e[i,1]] then

    begin

      i:=next[i];

      continue;

    end;

    v[e[i,1]]:=true;

    dis[e[i,1]]:=dis[x]+e[i,2];

    f[e[i,1],0]:=x;

    dfs(e[i,1],y+1);

    i:=next[i];

  end;

end;

procedure init;

var

  i,j,x,y,z:longint;

begin

  fillchar(e,sizeof(e),0);

  sum:=0;

  fillchar(f,sizeof(f),0);

  fillchar(dep,sizeof(dep),0);

  fillchar(v,sizeof(v),false);

  fillchar(last,sizeof(last),0);

  fillchar(next,sizeof(next),0); 

  fillchar(dis,sizeof(dis),0);

  readln(n,m);

  for i:=1 to n-1 do

  begin

    readln(x,y,z);

    add(x,y,z);

    add(y,x,z);

  end;

  dfs(1,1);

  for j:=1 to 31 do

    for i:=1 to n do

      f[i,j]:=f[f[i,j-1],j-1];

  for i:=1 to n do

    lg[i]:=trunc(ln(i)/ln(2));

end;

function lca(x,y:longint):longint;

var

  t,i:longint;

begin

  if dep[x]<dep[y] then

  begin

    t:=x;x:=y;y:=t;

  end;

  while (dep[x]>dep[y]) do x:=f[x,lg[dep[x]-dep[y]]];

  if x=y then exit(x);

  i:=lg[dep[x]];

  while i>=0 do

  begin

    if f[x,i]<>f[y,i] then

    begin

      x:=f[x,i];y:=f[y,i];

    end;

    dec(i);

  end;

  exit(f[x,0]);

end;

begin

  readln(t);

  for i:=1 to t do

  begin

    init;

    for j:=1 to m do

    begin

      readln(x,y);

      writeln(dis[x]+dis[y]-dis[lca(x,y)]*2);

    end;

  end;

end.

 二、RMQ求LCA
        求树的dfs序（重复入队），两个结点第一次出现的位置之间的区间中结点的深度最小点即为LCA
        用RMQ求区间最小值，rmq=min(f[l,k],f[r-2^k+1,k])       （f[i,j]=min(f[i,j-1],f[i+2^(j-1),j-1]）
        注意：要求的是深度最小的点，而RMQ求的是深度，所以可以在f中记录点，单独用深度dep[x]比较后转移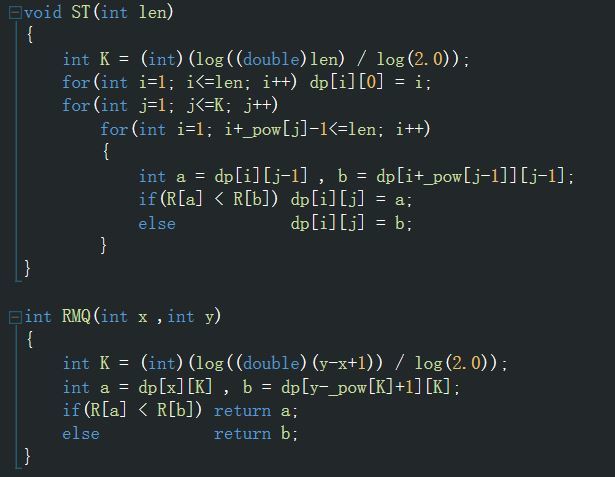

 

匈牙利算法模板

const
  maxn=1000;
  maxm=600000;

var
  a,match:array[1..maxn*2]of longint;
  e,next,last:array[1..maxm]of longint;
  n,m,me,sum:longint;
  v:array[1..maxn*2]of boolean;

procedure add(x,y:longint);
begin
  inc(sum);
  e[sum]:=y;
  next[sum]:=last[x];
  last[x]:=sum;
end;

procedure init;
var
  i,x,y:longint;
begin
  readln(n,m,me);
  for i:=1 to me do
  begin
    readln(x,y);
    if y>m then continue;
    add(x,y+n);
    add(y+n,x);
  end;
end;

function dfs(x:longint):boolean;
var
  i,go:longint;
begin
  i:=last[x];
  while i>0 do
  begin
    go:=e[i];
    if not v[go]  then
    begin
      v[go]:=true;
      if (match[go]=0)or(dfs(match[go])) then
      begin
        match[go]:=x;
        match[x]:=go;
        exit(true);
      end;
    end;
    i:=next[i];

  end;
  exit(false);
end;

function hungarian:longint;
var
  i:longint;
begin
  hungarian:=0;
  for i:=1 to n do
    if match[i]=0 then
    begin
      fillchar(v,sizeof(v),false);
      if dfs(i) then inc(hungarian);
    end;
end;

begin
  init;
  writeln(hungarian);
end.