机器学习之KNN

以下博客主要由两部分构成。一是理论讲解，而是代码实现（因为工程上使用KNN的频率不是很高，所以代码不是目的，一些代码中的技巧就显得很重要了）。

理论分析

首先KNN是什么？K-Nearest Neighbors (KNN)
以下的图片均来自‘贪心科技’，不是打广告，纯粹是尊重知识产权。

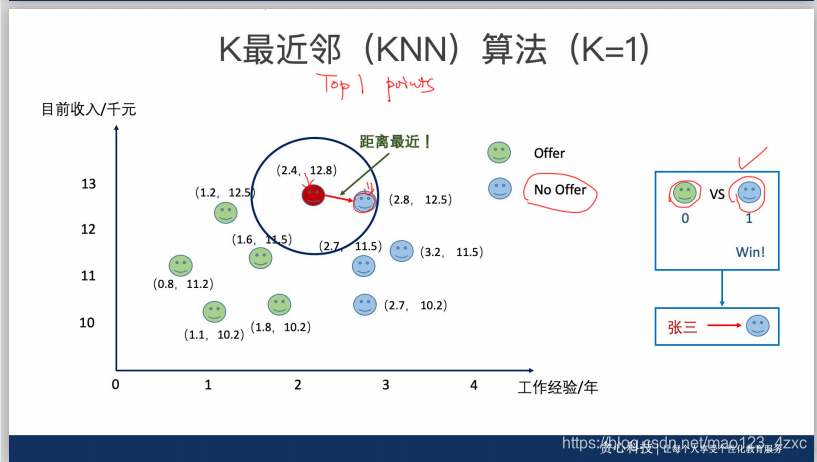
问题一：为什么一般大家会选择奇数的K
因为便于投票分类
决策边界决定了“线性分类器”或者“非线性分类器”
怎么选择合适的K，一般会用交叉验证法来选择合适的K。同时哟啊注意，不要用测试数据来调参。

特征缩放----线性归一化（Min-max Normalization）
$X_{new}=(X-min(X))÷(max(X)-min(X))$

标准差标准化 (Z-score Normalization)
就是平均值、方差啥的
$X_{new}=(X-mean(X))÷(std(X))$
KNN之所以不能广泛的工程应用的是因为KNN处理大数据量的任务困难，主要困难在耗时、K值选择影响太大。

代码

主要代码可以看我的github(来都来了，打颗星啊)
KNN

sklearn划分数据

sklearn划分数据
from sklearn.model_selection import train_test_split
#把数据分为训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003)
'''
参数代表含义:
train_data：所要划分的样本特征集
train_target：所要划分的样本结果
test_size：样本占比，如果是整数的话就是样本的数量
random_state：是随机数的种子。
'''

统计非0数目

np.count_nonzero()

反函数 np.argsort

import numpy as np
x=np.array([1,4,3,-1,6,9])
y = x.argsort()
#y=array([3,0,2,1,4,5])
#我们发现argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)，然后输出到y。例如：x[3]=-1最小，所以y[0]=3,x[5]=9最大，所以y[5]=5。

计数 count.most_common

from collections import Counter
#统计字符串
# top n问题
user_counter = Counter("abbafafpskaag")
print(user_counter.most_common(3)) #[('a', 5), ('b', 2), ('f', 2)]
print(user_counter['a']) # 5
#总结：most_common()函数用来实现Top n 功能.

生成随机样本、数据拼接

# 生成一些随机样本
n_points = 100
#依据指定的均值和协方差生成数据
X1 = np.random.multivariate_normal([1,50], [[1,0],[0,10]], n_points)
X2 = np.random.multivariate_normal([2,50], [[1,0],[0,10]], n_points)
#数据拼接
X = np.concatenate([X1,X2])

product

import itertools
a = (1, 2, 3)
b = ('A', 'B', 'C')
c = itertools.product(a,b)
for elem in c:
    print(elem)
(1, 'A')
(1, 'B')
(1, 'C')
(2, 'A')
(2, 'B')
(2, 'C')
(3, 'A')
(3, 'B')
(3, 'C')

还有一些生成热图的其他代码请看github