【机器学习期末总结】7-决策树

特征选择
树生成
树剪枝

决策树

决策树分类

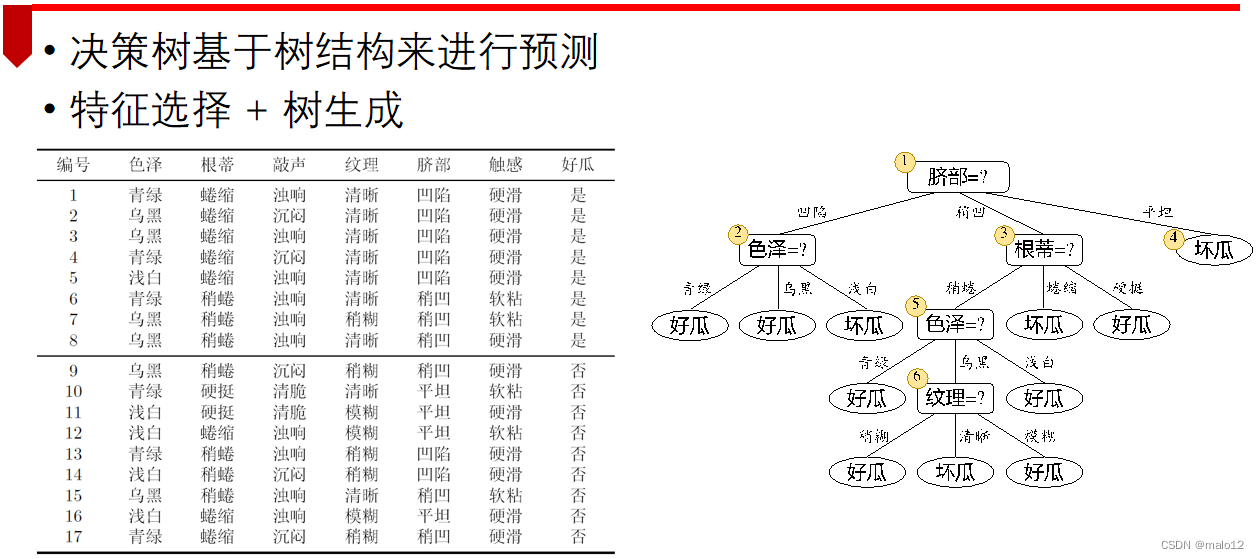
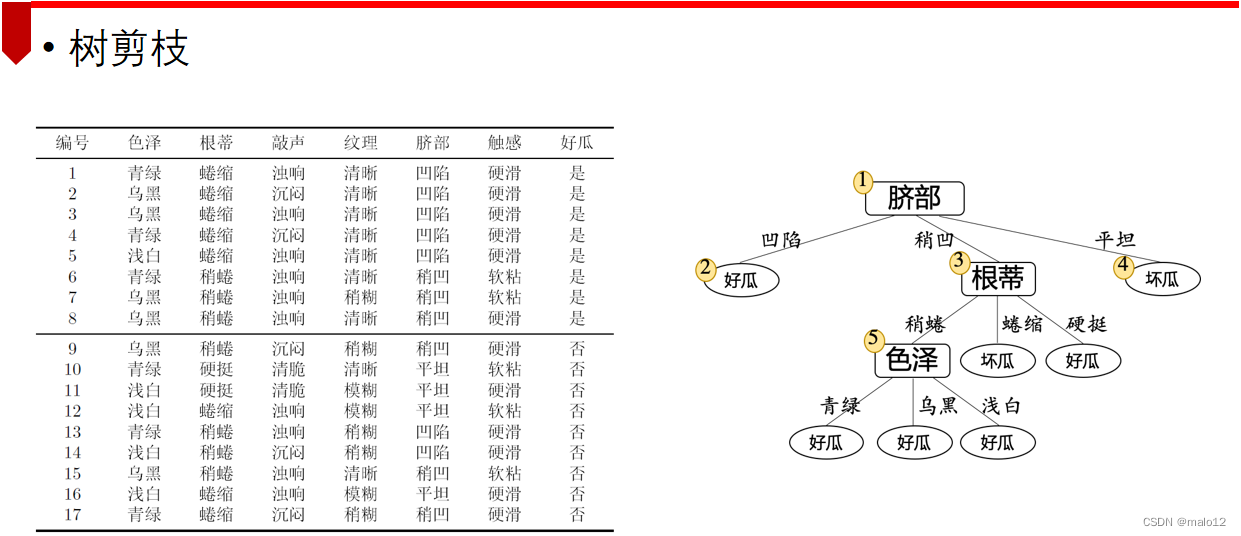
决策树回归

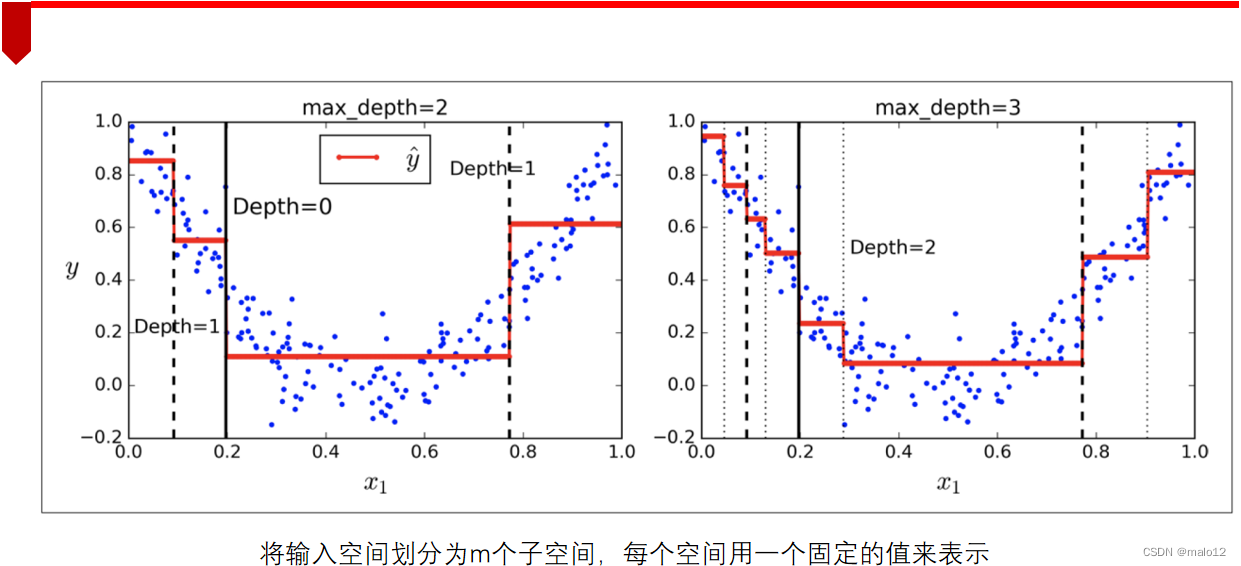
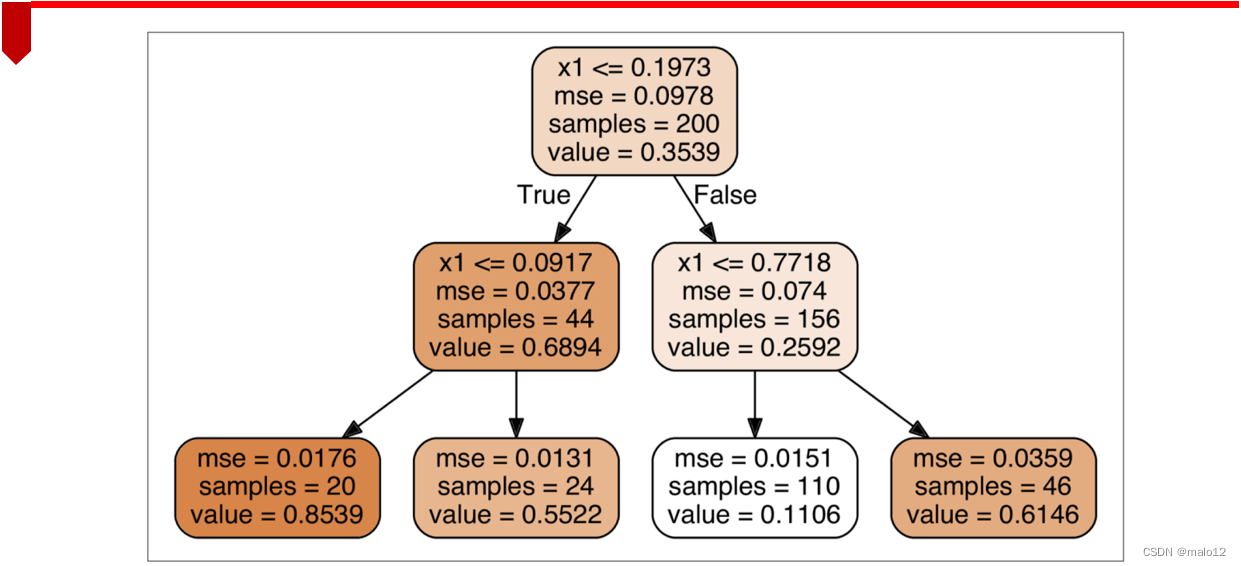
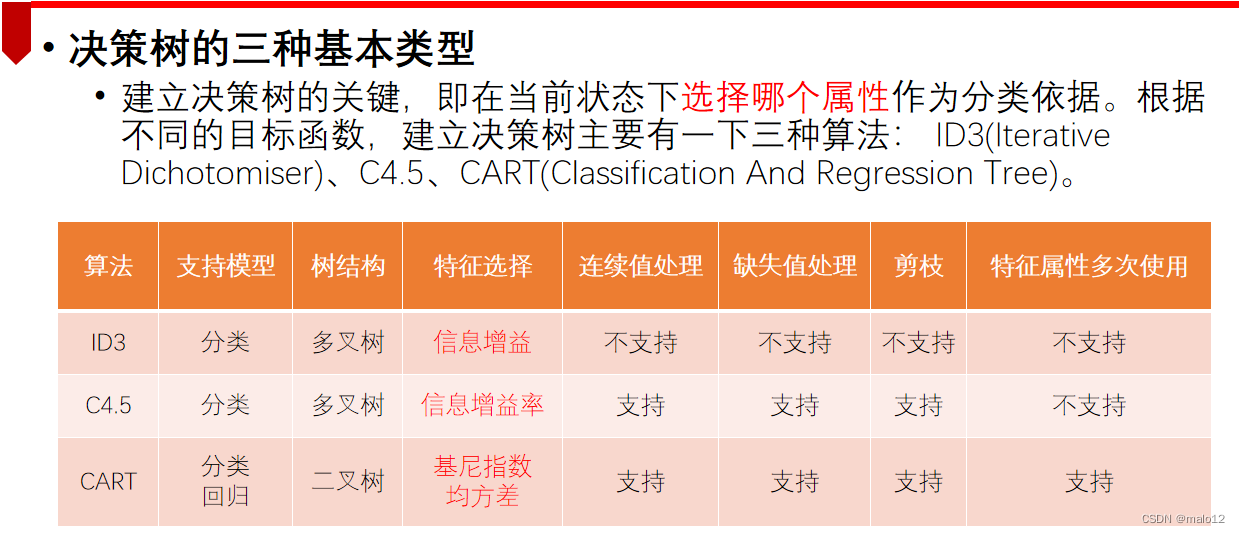
决策树类型

特征选择

特征选择在于选取对训练数据具有分类能力的特征
经典的特征选择方法：

• 信息增益
• 增益率
• 基尼指数

熵(Entropy)

条件熵

信息增益(Information Gain)

决策树的生成

ID3算法

基于信息增益准则选择特征，递归构建决策树

C4.5算法

基于信息增益比来选择特征

CART算法

Classification And Regression Tree

• 可用于分类，也可以用于回归
• CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”
• 左分支取值为“是”的分支，右分支取值为“否”的分支
• CART算法分为两步：
  决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大
  决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这是用损失函数最小最为剪枝的标准
• 决策树的生成就是递归地构建二叉决策树的过程
• 回归树特征选择
  平方误差最小化准则
• 分类树特征选择
  基尼指数（Gini index）最小化准则

分类树的生成

用基尼指数选择最优特征，同时决定该特征的最优二值切分点

回归树的生成

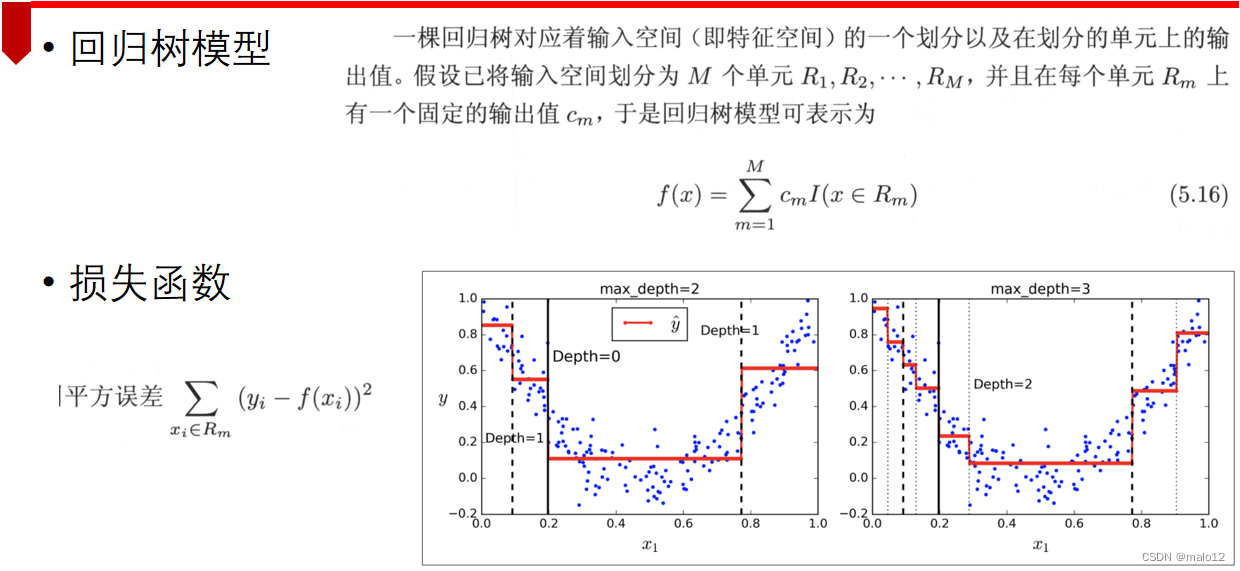
算法：最小二乘回归树生成算法

*CART剪枝算法

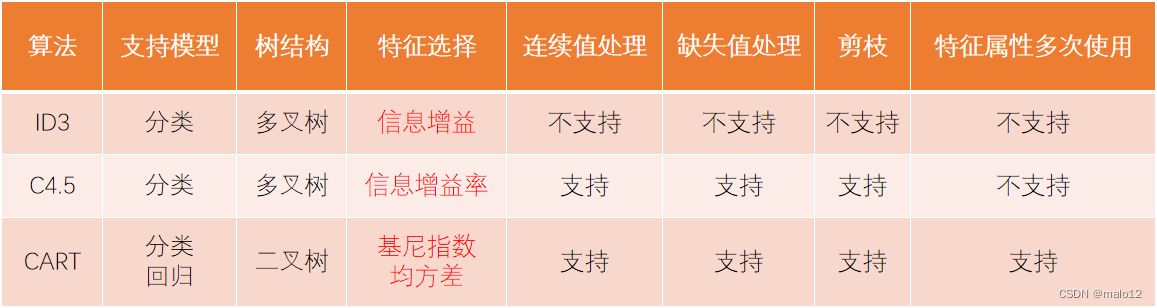
三种算法的比较

决策树的剪枝

• 决策树生成算法递归地产生决策树，直到不能继续下去为止
  这种方法容易产生过拟合问题
• 剪枝策略
  基于训练集的剪枝
  基于验证集的剪枝

基于训练集的剪枝

• 考虑决策树的复杂度，对已生成的决策树进行简化
• 剪枝操作
  从已生成的树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型
  
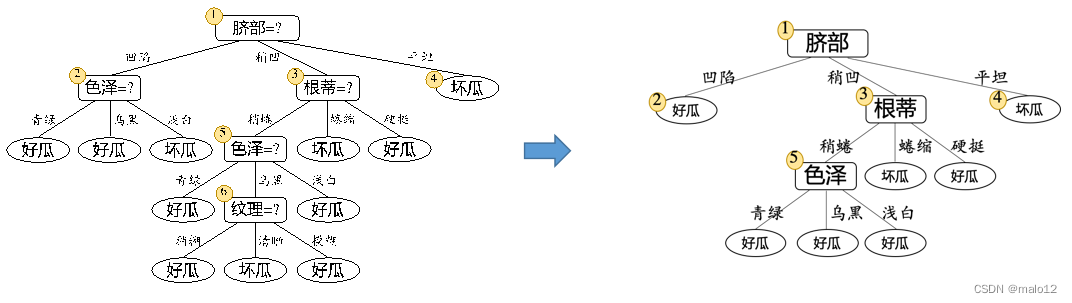
• 极小化决策树整体的损失函数

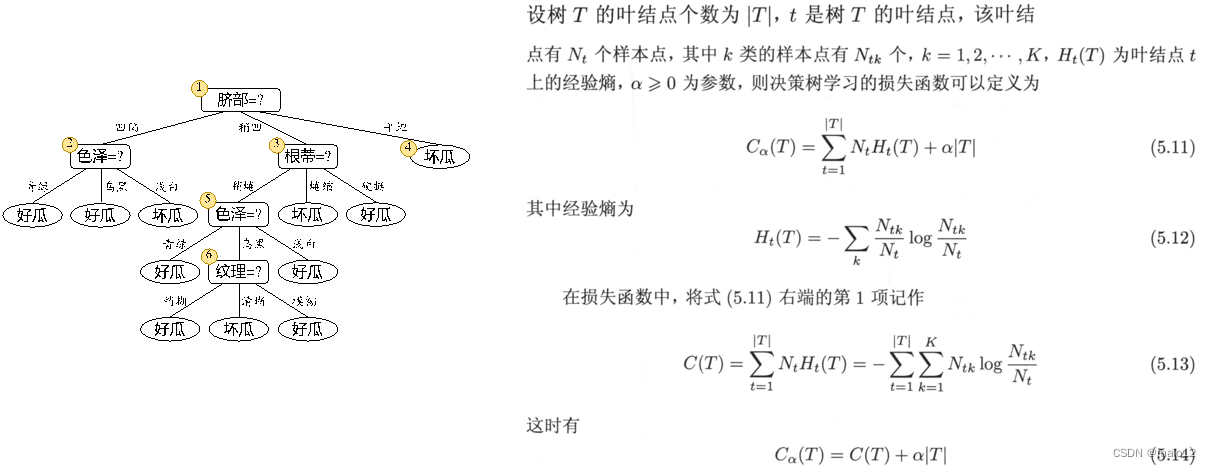
基于验证集的剪枝

• 判断决策树泛化性能是否提升的方法
  留出法：预留一部分数据用作“验证集”以进行性能评估

• 剪枝的基本策略

预剪枝

决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点记为叶结点，其类别标记为训练样例数最多的类别

针对上述数据集，基于信息增益准则，选取属性“脐部”划分训练集。分别计算划分前（即直接将该结点作为叶结点）及划分后的验证集精度，判断是否需要划分。若划分后能提高验证集精度，则划分，对划分后的属性，执行同样判断；否则，不划分

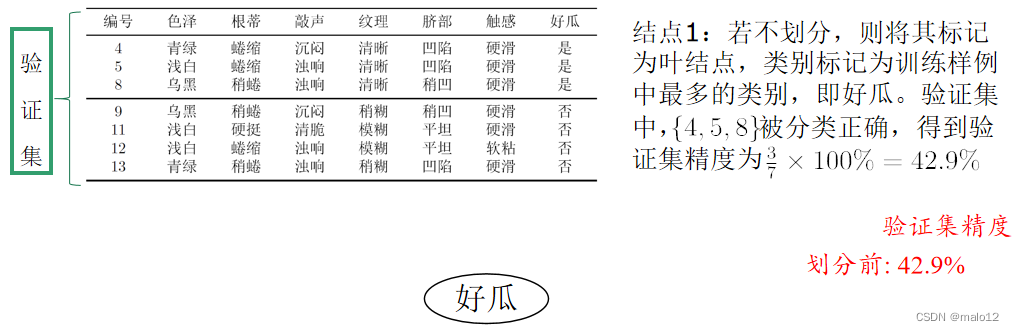
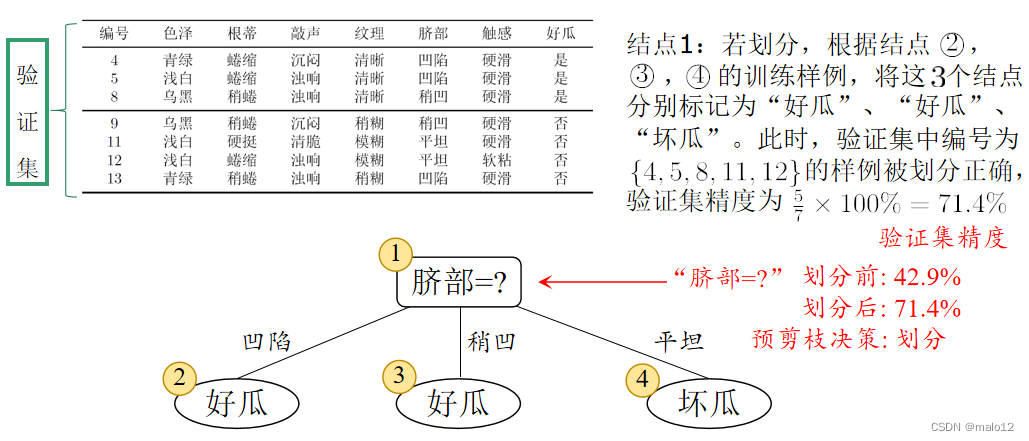
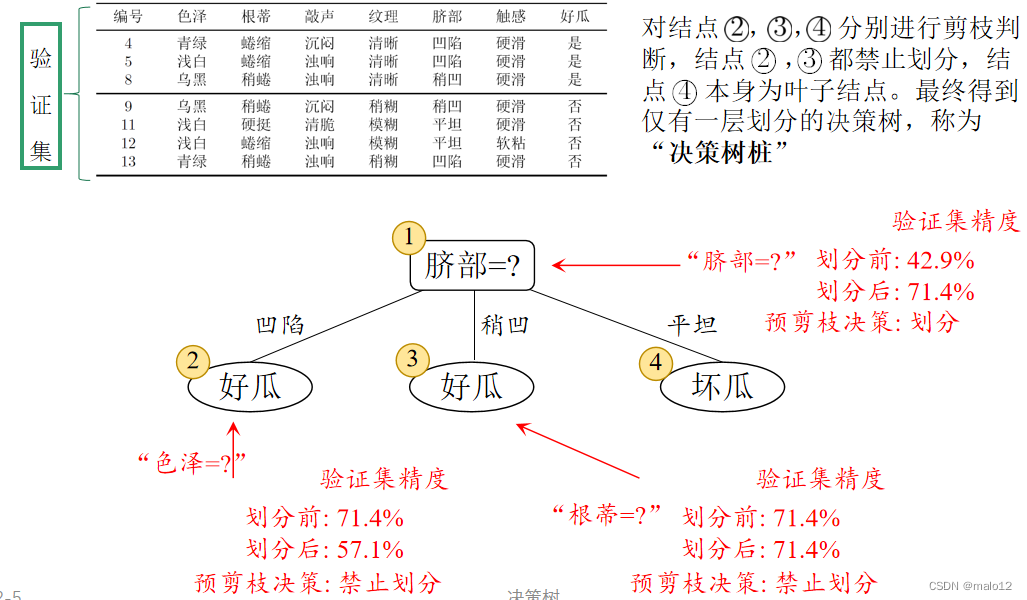
预剪枝的优缺点

• 优点
  降低过拟合风险
  显著减少训练时间和测试时间开销

• 缺点
  欠拟合风险：有些分支的当前划分虽然不能提升泛化性能，但在其基础上进行的后续划分却有可能导致性能显著提高。预剪枝基于“贪心”本质禁止这些分支展开，带来了欠拟合风险

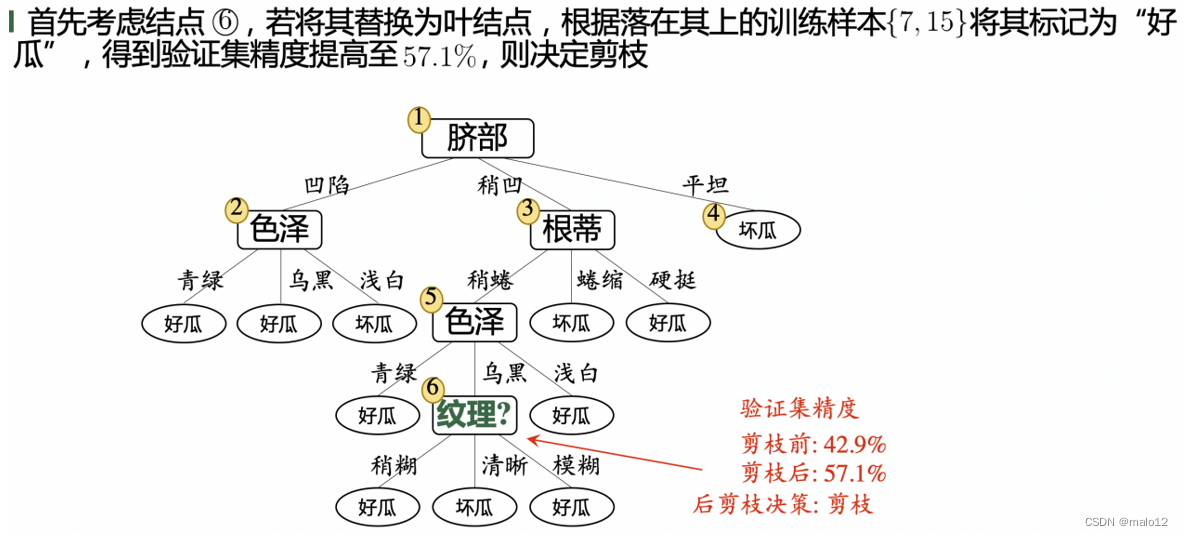
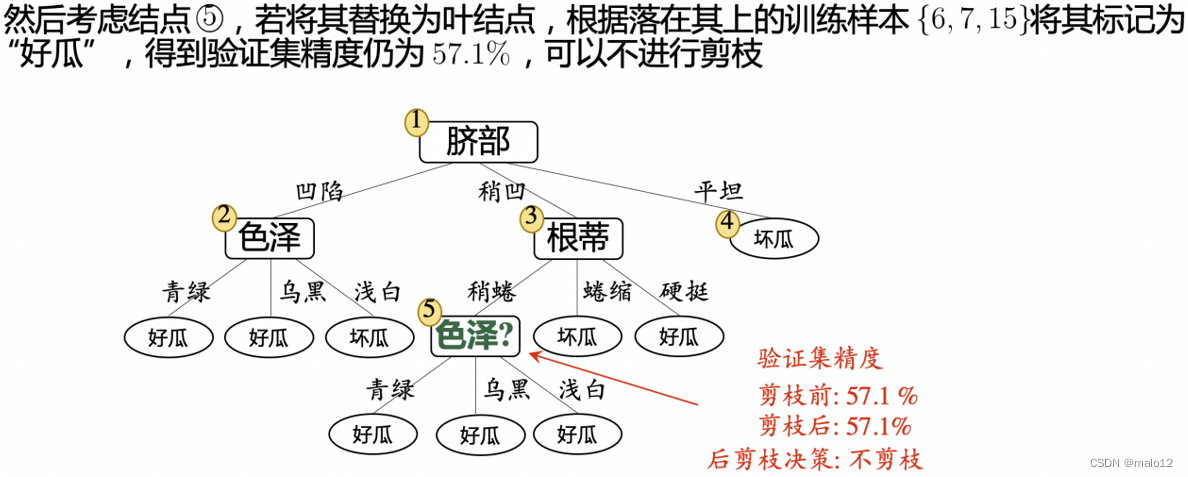
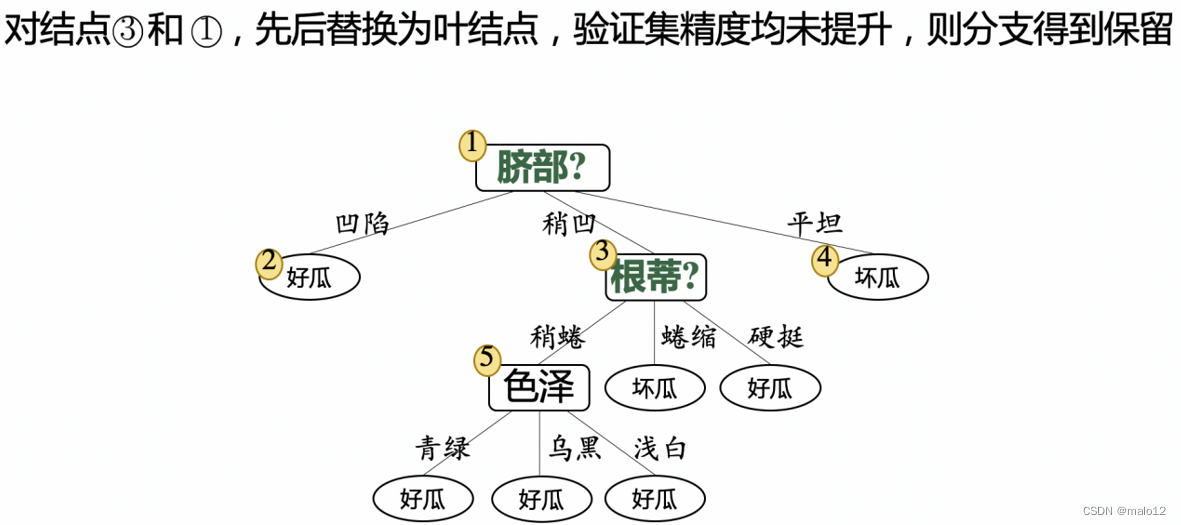
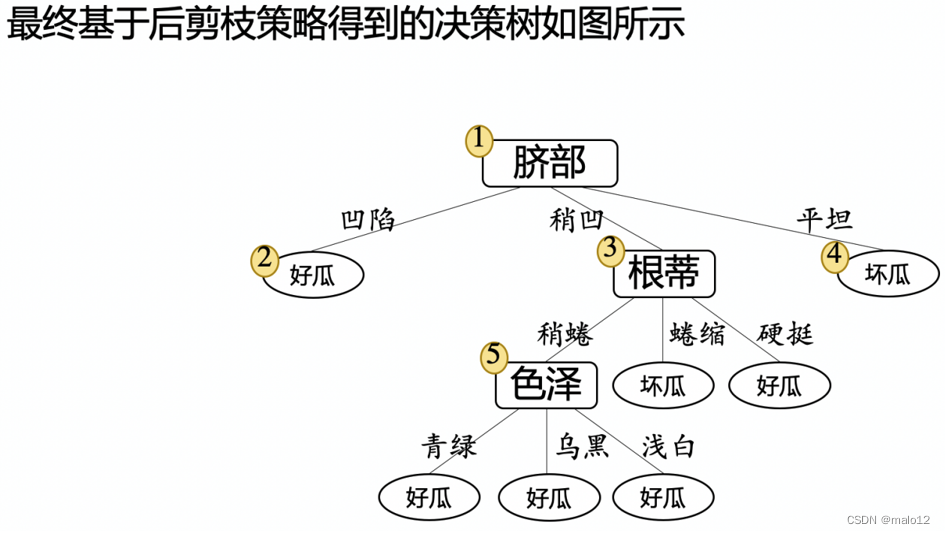
后剪枝

先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点

后剪枝的优缺点

• 优点
  后剪枝比预剪枝保留了更多的分支，欠拟合风险小，泛化性能往往优于预剪枝决策树

• 缺点
  训练时间开销大：后剪枝过程是在生成完全决策树之后进行的，需要自底向上对所有非叶结点逐一考察

scikit-learn中的决策树

见官方文档

应用

机器学习实战教程（二）：决策树基础篇之让我们从相亲说起
机器学习实战教程（三）：决策树实战篇之为自己配个隐形眼镜
机器学习实战教程（十三）：树回归基础篇之CART算法与树剪枝