波前、PSF 与光路图：理解光学像差的三个视角

原创于 2025-09-28 15:34:27 发布 · 1.2k 阅读

CC 4.0 BY-SA版权

文章标签：

波前、PSF 与光路图：理解光学像差的三个视角

本文档旨在阐释光学系统中三种核心可视化工具——波前图 (Wavefront Map)、点扩散函数 (PSF) 和光路图 (Ray Schematic)——之间的深刻联系。通过并列展示常见的泽尼克 (Zernike) 像差在这三种形式下的表现，我们可以从波动光学、衍射物理和几何光学的角度全面理解像质的退化机理。

1. 如何解读每一行图

每一行代表一种特定的像差，并从左到右展示其三种不同但内在关联的物理图像。

左列: 波前 (Wavefront)

内容: 显示在归一化圆形光瞳（半径 $ρ=1\rho=1$ ）上的波前函数 $W(ρ,θ)W(\rho, \theta)$ 。其数值单位为“波长数”(waves)，即 $\mathrm{OPD}/\lambda$ 。
解读: 波前图描述了实际波前相对于理想球面波的偏离（即光学程差 OPD）。其形状直接决定了像差的类型和幅度。
- 外圈黑线是瞳面边界 (clear aperture)。在本套图中，归一化半径 $ρ=1\rho=1$ 对应物理孔径半径 $2.5\,\mathrm{mm}$ 。

中列: 点扩散函数 (PSF)

内容: 焦平面上的光强分布，即 $ \mathrm{PSF}(u,v) = \left|\mathcal{F}\left{P(x,y),e^{i2\pi W(x,y)}\right}\right|^2 $，其中 $P (x, y)$ 为圆形光瞳函数。
解读: PSF 是系统对点光源的衍射成像响应。它直观地展示了像差如何导致图像模糊、变形、拉伸或出现不对称的拖尾。图中显示的是放大的中心区域（窗口 0–20 $λ/D\lambda/D$ ）。

右列: 光路图 (Ray Schematic)

内容: 从光瞳出射的 61 条光线汇聚到焦平面附近的光路。图中范围为 $mm\pm7\,\mathrm{mm}$ 。
解读: 在几何光学近似下，光线方向垂直于波前。其偏转角由波前函数的梯度 (gradient) 决定。
- 对于沿 $s$ 方向的光线，其在焦平面 $X = f$ 上的位置 $y (f)$ 由初始位置 $s_0$ 和斜率 $θ(s0)\theta(s_0)$ 决定：
  $\theta(s_0) \approx -\frac{s_0}{f} + \frac{\partial\,\mathrm{OPD}(s_0)}{\partial s_0}, \quad y(f) = s_0 + \theta(s_0) \cdot f$
- 该图揭示了像差导致光线无法汇聚于一点的几何学机制，如形成线焦、弥散斑或非对称光斑。

统一物理参数

为便于比较不同像差的影响，所有图例均采用以下统一参数：

波长: $nm\lambda_0 = 550\,\mathrm{nm}$
孔径半径: $2.5\,\mathrm{mm}$
焦距: $5.0\,\mathrm{m}$
Zernike 系数 (RMS, waves): Tilt/Defocus = 1.0; Astig = 1.5; Coma/Spherical = 1.6; Tetrafoil = 1.2。

2. 基础理论：Zernike 多项式与成像

2.1 定义与正交性

Zernike 多项式是在单位圆盘 $ρ≤1\rho \le 1$ 上定义的一组完备正交基函数，非常适合描述圆形光瞳上的波前像差。

表达式:
$Z_n^{m}(\rho,\theta) = R_n^{|m|}(\rho) \times \begin{cases} \cos(m\theta), & m \ge 0 \\ \sin(|m|\theta), & m < 0 \end{cases}$
其中， $\ge |m|$ 且 $n - ∣ m ∣$ 为偶数。径向多项式 $Rnm(ρ)R_n^{m}(\rho)$ 定义为：
$R_n^{m}(\rho) = \sum_{k=0}^{(n-m)/2} (-1)^k \frac{(n-k)!}{k!\,[(n+m)/2-k]!\,[(n-m)/2-k]!} \rho^{n-2k}$
正交性: 它们在单位圆盘上带权重 $ρ\rho$ 的积分为零， $dθ∝δnn′δmm′\iint_{\rho\le1} Z_n^m Z_{n'}^{m'} \, \rho\,d\rho\,d\theta \propto \delta_{nn'}\delta_{mm'}$ ，这使得波前分解具有唯一性。

2.2 波前展开与单位

任意波前函数 $W(ρ,θ)W(\rho, \theta)$ 都可以展开为 Zernike 多项式的线性组合：
$W(\rho, \theta) = \sum_{n,m} c_n^m Z_n^m(\rho, \theta)$

系数 $c_n^m$ : 单位通常是“波长数 (waves)”，在报告中常以 RMS 值给出。
光学程差 (OPD): 物理长度单位下的像差为 $OPD(x,y)=λ⋅W(x,y)\mathrm{OPD}(x,y) = \lambda \cdot W(x,y)$ 。

2.3 “波前—PSF—光线”的核心联系

这三者之间的关系是光学成像物理的基石：

波前 $→\rightarrow$ PSF: 波前 $W$ 决定了光瞳面上的相位分布 $ei2πWe^{i2\pi W}$ 。根据傅里叶光学，PSF 是光瞳函数的傅里叶变换的模平方。波前的形状直接“雕刻”了远场衍射图样。
波前 $→\rightarrow$ 光线: 在几何光学近似下，光线的传播方向是波前的法线方向。因此，光线的偏折角度由波前梯度 $∇W\nabla W$ 决定。梯度越大的地方，光线偏折越剧烈。

结论: 同一种像差在三张图中的特征是同一物理本质的不同体现。例如：

线性梯度 (Tilt): 导致 PSF 整体平移和光线束整体偏转。
二次曲率 (Defocus, Astig): 改变光线的汇聚焦点，形成模糊或拉伸的 PSF。
非对称性 (Coma): 导致光线汇聚不均，形成单侧拖尾的彗星状 PSF。
高阶径向变化 (Spherical): 使不同环带的光线焦点分离，能量向外扩散形成环状 PSF。

3. 逐项解析：常见 Zernike 像差

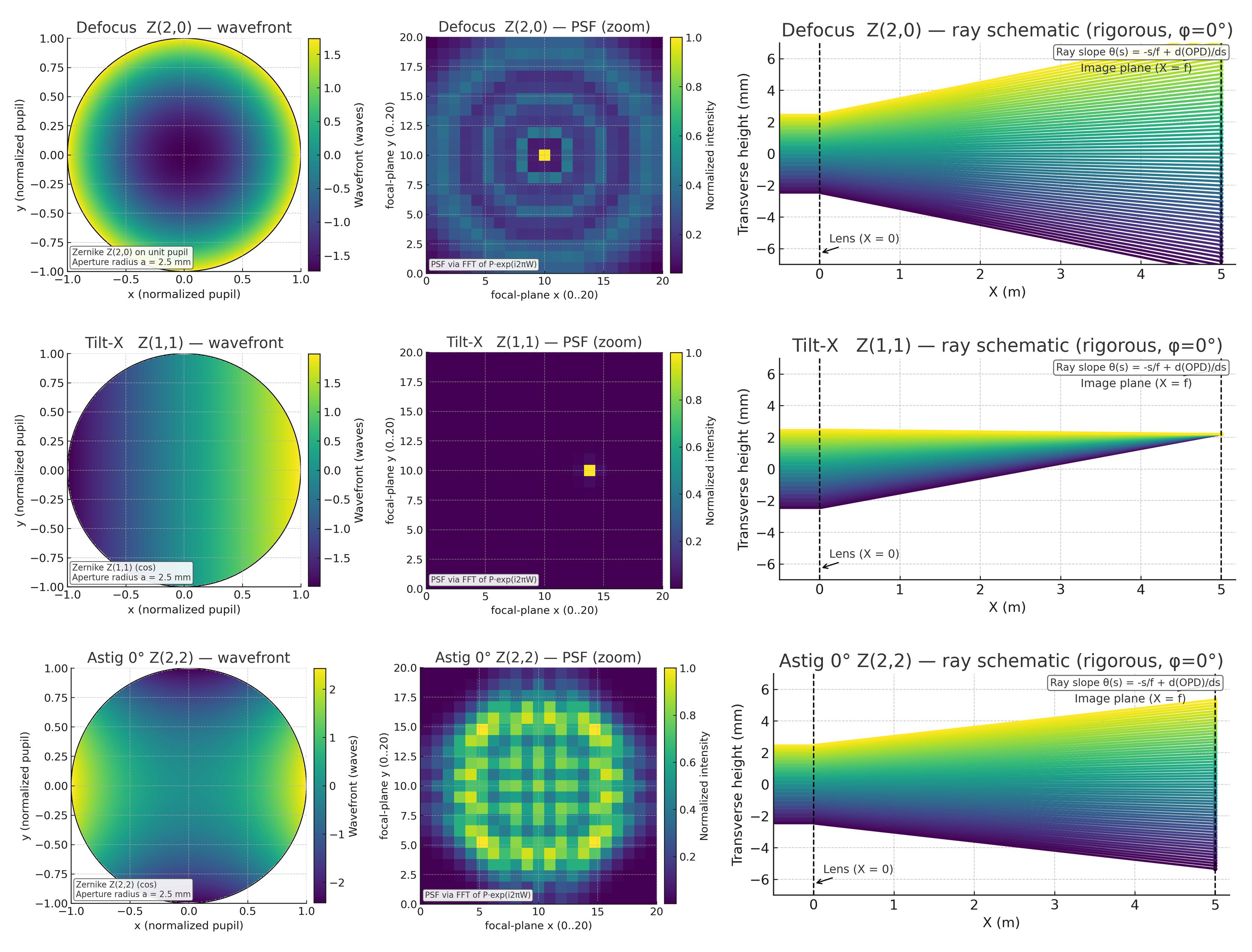
3.1 离焦 (Defocus) — $Z_2^0$

波前: 轴对称的二次抛物面。
PSF: 能量从中心向外扩散，形成经典的“艾里斑”旁瓣增强或环状结构，保持圆对称。
光线: 所有光线仍汇聚于一点，但该点在光轴上偏离了理想焦平面，导致在焦平面上形成一个均匀的弥散斑。光线斜率 $θ(s0)=−s0/feff\theta(s_0) = -s_0/f_{\mathrm{eff}}$ ，其中有效焦距 $fefff_{\mathrm{eff}}$ 发生了改变。

3.2 倾斜 (Tilt-X) — $Z_1^1$

波前: 沿 X 方向的线性斜坡，相位呈偶极分布。
PSF: 形状和大小与无像差时完全相同（艾里斑），但中心位置发生了平移。
光线: 整束光线被同向偏转一个固定角度 $θ0\theta_0$ ，导致焦点在像面上整体平移。斜率 $θ(s0)=−s0/f+θ0\theta(s_0) = -s_0/f + \theta_0$ 。

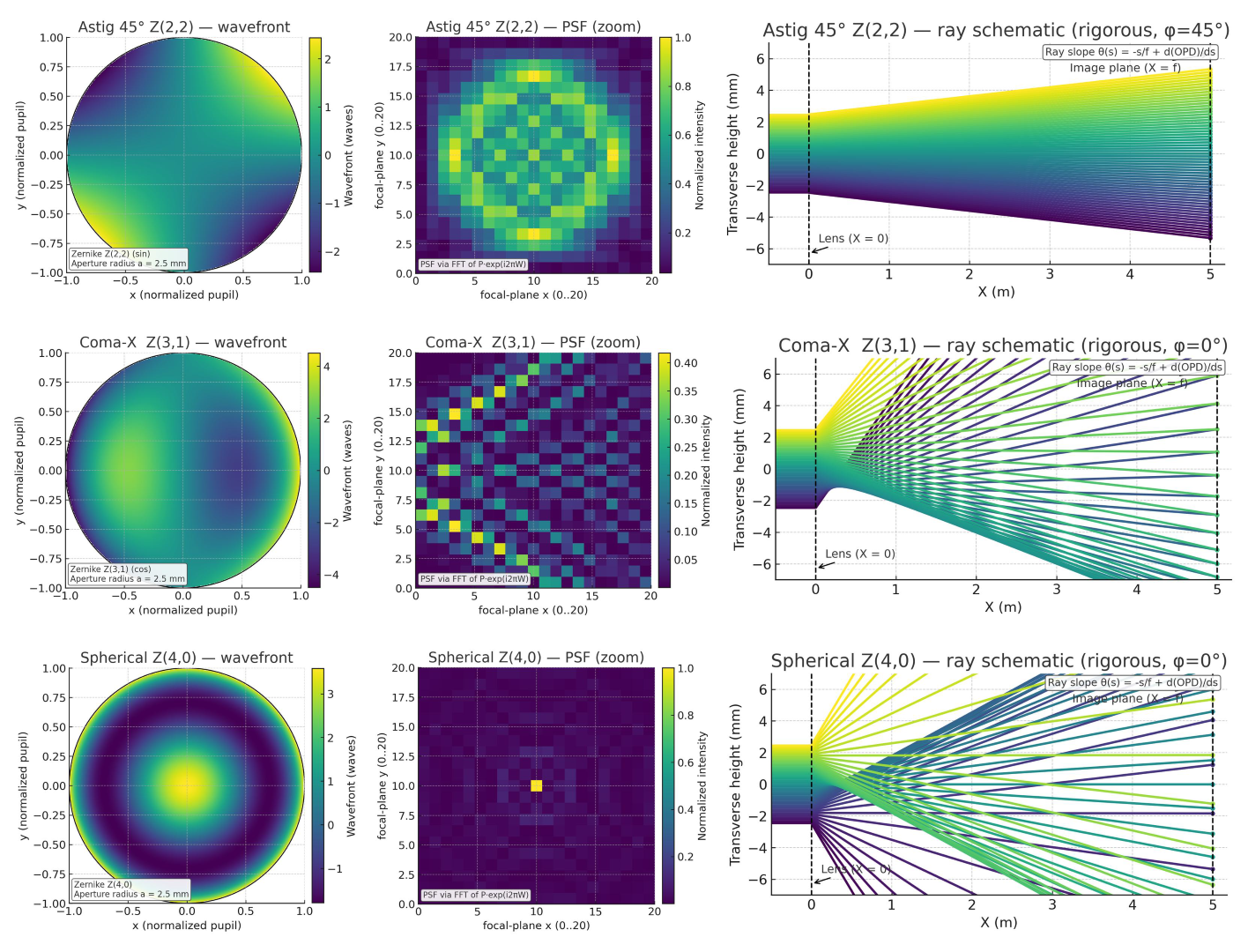
3.3 像散 (Astigmatism, 0°) — $Z_2^2$

波前: 鞍形表面，具有两个正交的主轴，曲率相反（四极对称）。
PSF: 沿一个主轴方向拉长，形成线状或椭圆光斑。在两个线焦之间，光斑呈圆形（此时为最小弥散斑）。
光线: 水平和垂直方向的光线分别汇聚在光轴上不同的位置，形成两个相互垂直的“线焦”。在理想焦平面上，光线形成一个椭圆形的弥散斑。
- 主截面有效焦距: $feff=f/(1∓β)f_{\mathrm{eff}} = f / (1 \mp \beta)$

3.4 彗差 (Coma-X) — $Z_3^1$

波前: 具有奇次对称性（一侧陡峭，一侧平缓）。
PSF: 能量向一侧集中并拖出一条“彗星”状的尾巴，严重破坏图像的对称性。
光线: 来自光瞳不同区域的光线汇聚到像平面上不同的高度，形成一个“V”形或彗星状的光斑。中心光线和边缘光线的焦点不重合。
- 斜率模型: $θ(s0)≈−s0/f+tilt+c⋅s02\theta(s_0) \approx -s_0/f + \text{tilt} + c \cdot s_0^2$

3.5 球差 (Spherical) — $Z_4^0$

波前: 轴对称的四次函数，中心平坦，边缘陡峭。
PSF: 中心峰值能量下降，能量被分散到周围的衍射环中，导致图像对比度降低和模糊。
光线: 来自光瞳边缘的光线比来自中心区域的光线更早地汇聚在光轴上。在任何一个像面上都无法形成清晰的点，而是形成一个弥散斑。
- 斜率模型: $θ(s0)≈−s0/f⋅(1+k⋅s02)\theta(s_0) \approx -s_0/f \cdot (1 + k \cdot s_0^2)$

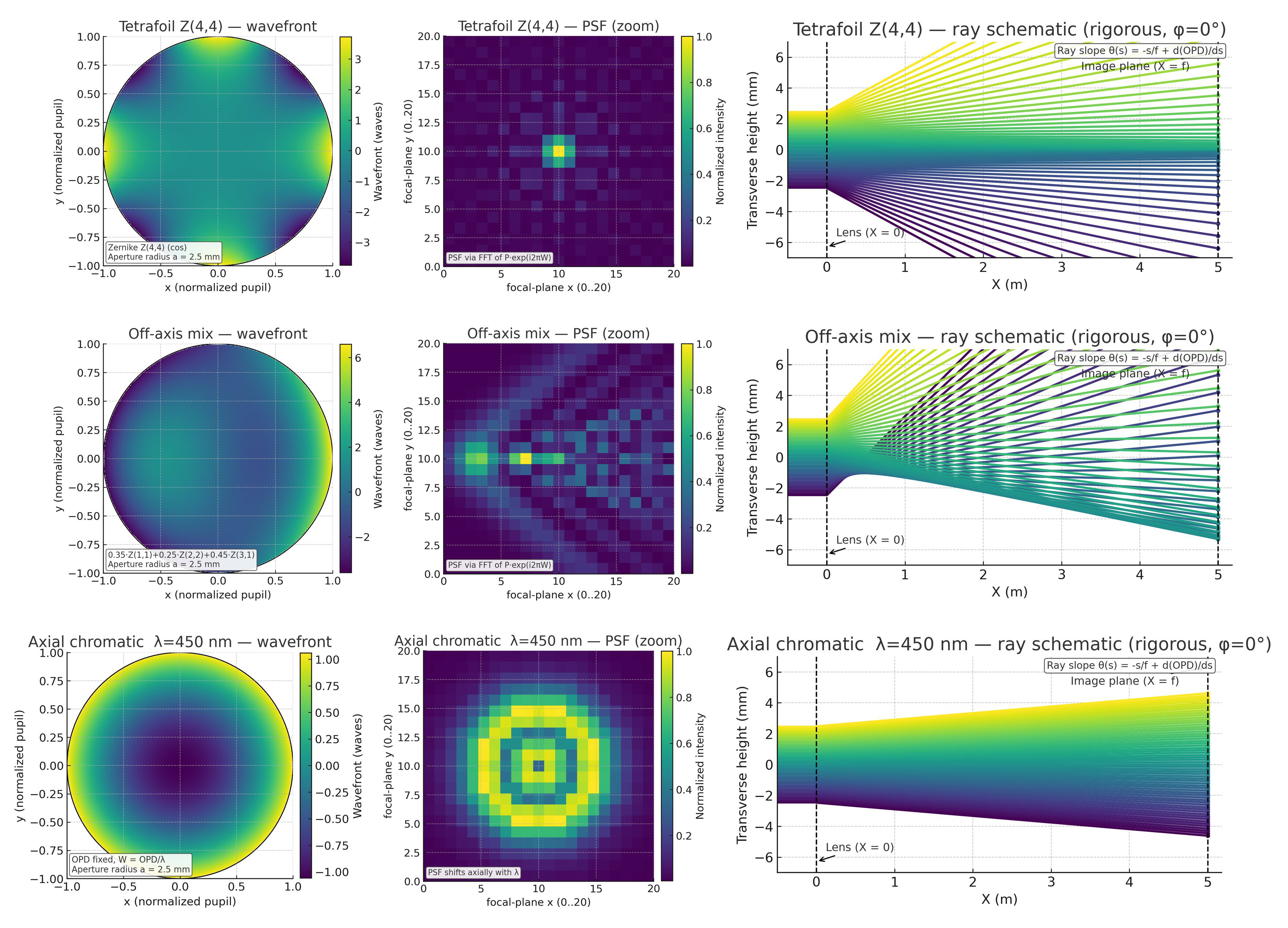
3.6 四叶草 (Tetrafoil, 0°) — $Z_4^4$

波前: 具有四重旋转对称性（ $∣ m ∣ = 4$ ），形态如四叶草。
PSF: 光斑分裂成四个主要瓣，呈方形或星芒状。
光线: 光线汇聚模式复杂，形成具有四重对称性的弥散图形。
- 切片上的斜率模型: $θ(s0)≈−s0/f+t⋅s03\theta(s_0) \approx -s_0/f + t \cdot s_0^3$

3.7 离轴组合 (Off-axis Combination)

构成: 实际的离轴视场通常是多种像差的组合，主要是倾斜 (Tilt) + 像散 (Astig) + 彗差 (Coma)。
PSF: 表现为多种效应的叠加：整体偏移、沿某个方向拉伸、并带有单侧拖尾。
光线: 焦点偏移，且光斑形状既不对称也不呈简单椭圆，是像散和彗差几何特征的混合体。

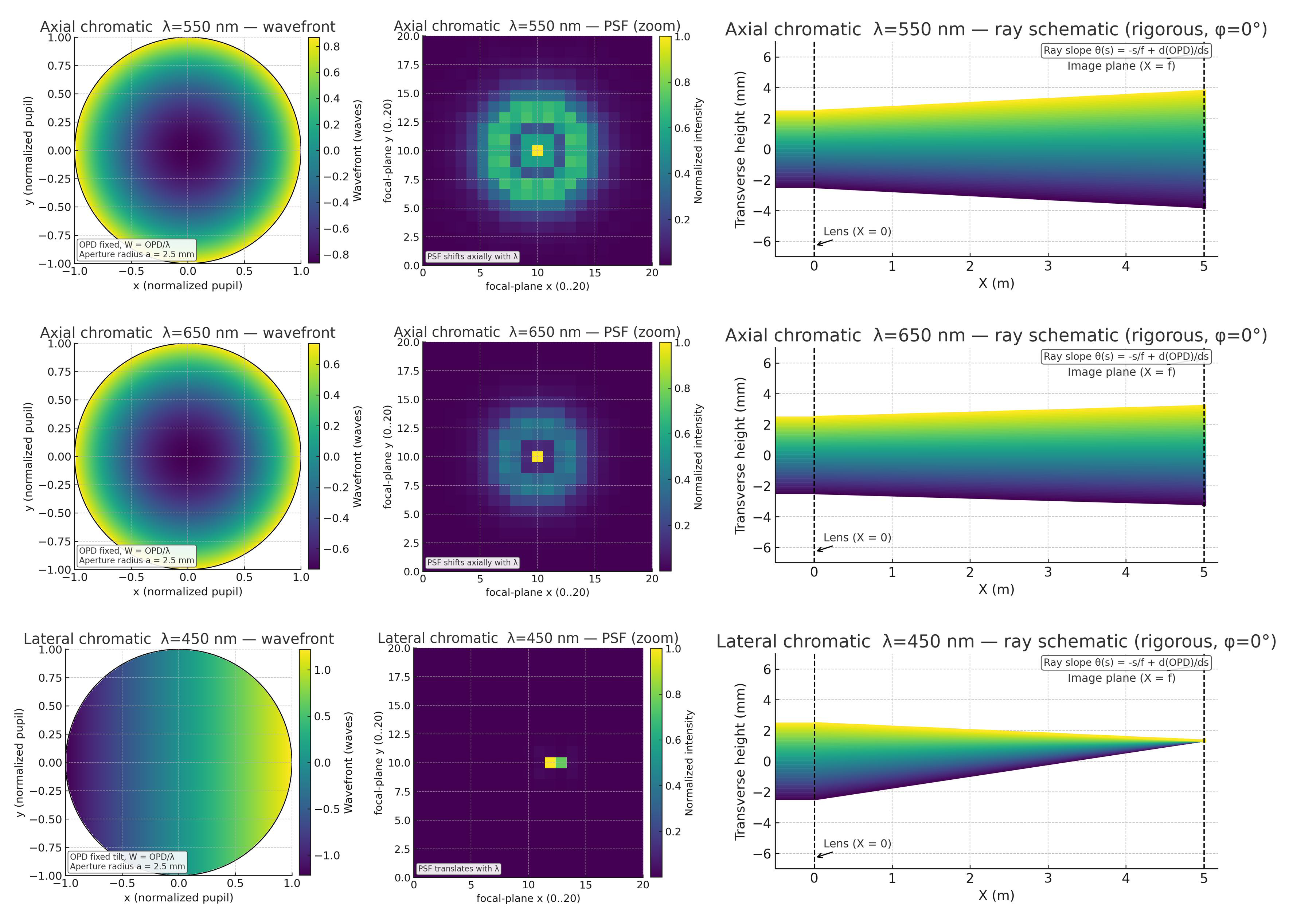
3.8 色差 (Chromatic Aberration)

色差与 Zernike 模式不同，它源于材料折射率对波长的依赖性。

轴向色差 (Axial): 不同颜色的光焦点沿光轴前后分离 ( $f=f(λ)f=f(\lambda)$ )。在固定像面上，一些颜色聚焦而另一些则离焦。
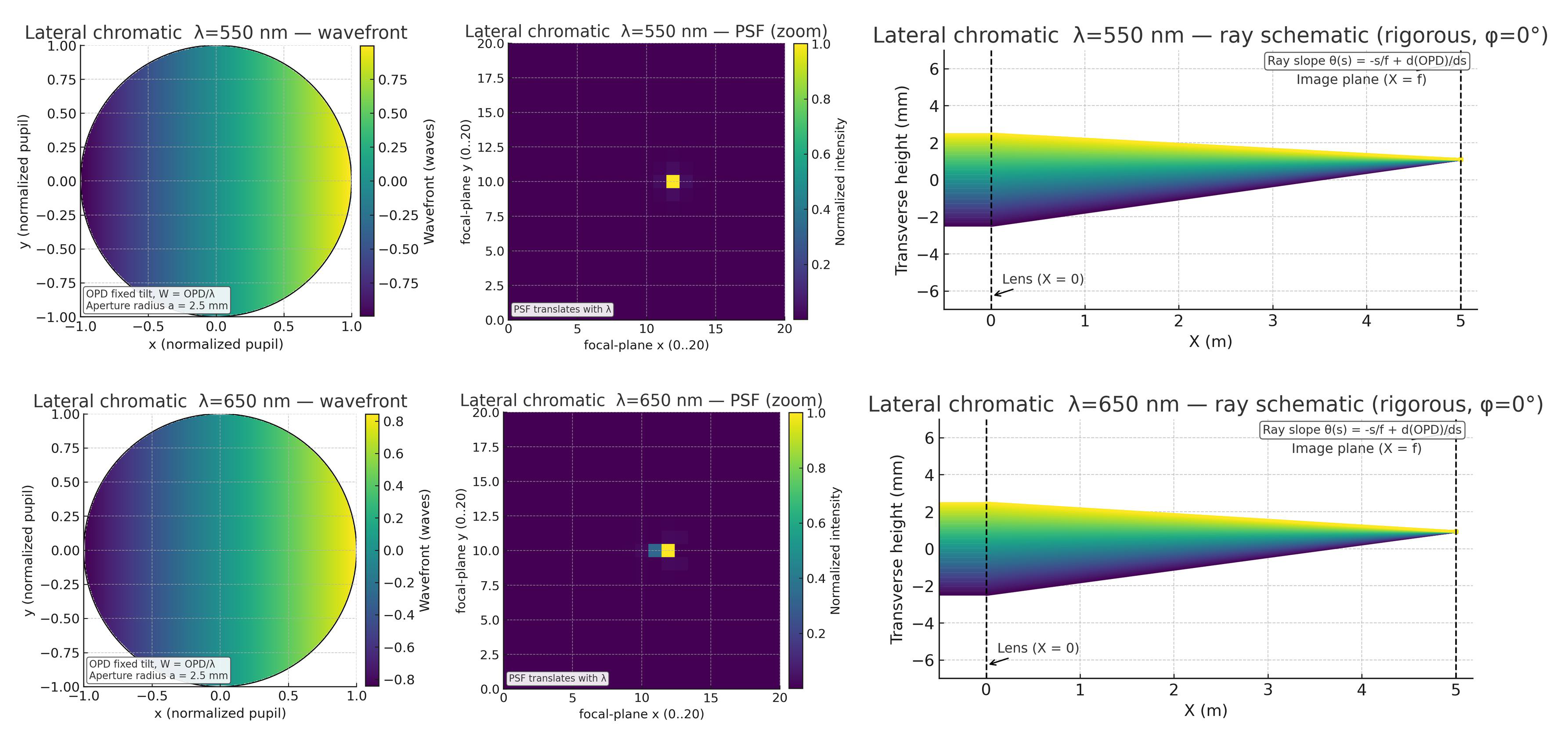
横向色差 (Lateral): 不同颜色的光在像平面上的放大率不同，导致像高不同 ( $θ=θ(λ)\theta = \theta(\lambda)$ )，点光源会色散成一个微小的彩虹光谱。

4. 常见问题 (FAQ)

Q1: 波前图中的那个“圆”到底是什么？

A: 它是光学系统的光瞳 (pupil) 在归一化坐标下的表示。所有进入系统的光线都必须通过这个圆形孔径。波前像差就是定义在这个圆域上的函数。

坐标对应: 归一化半径 $ρ=1\rho=1$ 对应物理孔径的边缘，即半径 $2.5\,\mathrm{mm}$ 。

Q2: 为什么波前图是平滑的，而我看过一些相位图是带“条纹”的？

A: 本文档的波前图展示的是未包裹 (unwrapped) 的物理量 $\mathrm{OPD}/\lambda$ ，它是一个连续的实数函数，其梯度直接对应光线斜率。

而参与衍射计算的相位是 $ϕ=2πW\phi = 2\pi W$ 。如果我们将 $ϕ\phi$ 的值限制在 $2\pi)$ 区间内进行可视化，就会得到带有不连续“跳变”或“条纹”的包裹相位图 (wrapped phase)。两者在物理上是等效的（因为 $eiϕ=ei(ϕ+2kπ)e^{i\phi} = e^{i(\phi+2k\pi)}$ ），但未包裹的波前图在与几何光学和 Zernike 系数关联时更为直观。

5. 工程实践提示

Maréchal 准则: 当波前方的 RMS 值 $σW≲λ/14\sigma_W \lesssim \lambda/14$ 时，斯特列尔比 (Strehl Ratio) $\approx e^{-(2\pi\sigma_W)^2} \gtrsim 0.8$ 。此时系统可被认为是“衍射受限”的，像差影响较小。
模型近似: 本文中的 PSF 基于标量夫琅禾费衍射理论和均匀圆形光瞳。真实的系统若有中心遮挡、蜘蛛臂支撑或非圆形光圈，其 PSF 的细节（如衍射环和尖峰）会发生显著变化。光线图也采用了小角近似和薄透镜模型，旨在教学演示几何趋势。
MTF: 点扩散函数 (PSF) 的傅里叶变换是光学传递函数 (OTF)，其模值——调制传递函数 (MTF)——是评价系统对不同空间频率细节传递能力的关键指标。宽而弥散的 PSF 对应着快速衰减的 MTF。