目录
3.3 最小外接圆(Minimum Enclosing Circle)
一、图像梯度处理
1. 什么是图像梯度?
图像梯度可以简单理解为图像像素值(灰度值)在某个方向上的变化率(类似数学上的导数):
-
梯度方向:灰度变化最大的方向(即边缘的方向垂直线)
-
梯度幅值:灰度值变化的快慢,值越大表示变化越明显(可能是边缘)
图像梯度就是——图像中像素亮度变化的快慢和方向。
你可以把它想象成在一张图像上“摸”地形的感觉:
如果亮度变化平稳,摸起来就像平地;
如果亮度突然变得很亮或很暗,就像遇到了一个“陡坡”——这就是边缘;
图像梯度就是帮我们找到这些“坡”,也就是图像中“变化剧烈”的地方。
2. 梯度的数学形式
对于一个灰度图像 $f(x, y)$,在位置 $(x, y)$ 处的图像梯度可以表示为二维向量:
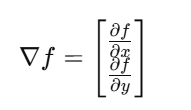
-
$\frac{\partial f}{\partial x}$ 表示水平方向的变化(横向边缘)
-
$\frac{\partial f}{\partial y}$ 表示垂直方向的变化(纵向边缘)
模拟一张灰度图:
import cv2 as cv
import numpy as np
# 模拟一张图像,灰度图
img=np.array([[100,102,109,110,98,20,19,18,21,22],
[109,101,98,108,102,20,21,19,20,21],
[109,102,105,108,98,20,22,19,19,18],
[109,98,102,108,102,20,23,19,20,22],
[109,102,105,108,98,20,22,19,20,18],
[100,102,108,110,98,20,19,18,21,22],
[109,101,98,108,102,20,22,19,20,21],
[109,102,108,108,98,20,22,19,19,18],
],dtype=np.float32)
# 定义卷积核,
kernel=np.array([[-1,0,1],
[-2,0,2],
[-1,0,1]],dtype=np.float32)
# 二维卷积操作
img2=cv.filter2D(img,-1,kernel)
# 打印卷积后的图
print(img2)输出:
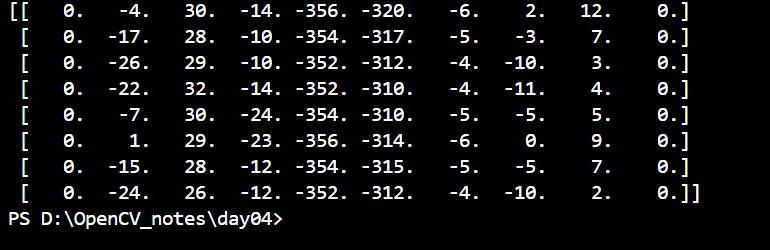
3.常见的梯度计算方法(近似求导)
由于图像是离散的,所以我们常用卷积的方式近似求导。
3.1 Sobel算子
加权平滑,抗噪能力强:
Sobel-X: Sobel-Y:
[-1 0 +1] [-1 -2 -1]
[-2 0 +2] [ 0 0 0]
[-1 0 +1] [+1 +2 +1]上面的两个卷积核都叫做Sobel算子,只是方向不同,它先在垂直方向计算梯度
再在水平方向计算梯度:
最后求出总梯度:
在梯度处理方式这个组件中,当参数filter_method选择Sobel时,其他参数的含义如下所述:
**sobel_image = cv2.Sobel(src, ddepth, dx, dy, ksize)**
**src**:这是输入图像,通常应该是一个灰度图像(单通道图像),因为 Sobel 算子是基于像素亮度梯度计算的。在彩色图像的情况下,通常需要先将其转换为灰度图像。
**ddepth**:这个参数代表输出图像的深度,即输出图像的数据类型。在 OpenCV 中,-1 表示输出图像的深度与输入图像相同。
**dx,dy**:当组合为dx=1,dy=0时求x方向的一阶导数,在这里,设置为1意味着我们想要计算图像在水平方向(x轴)的梯度。当组合为 dx=0,dy=1时求y方向的一阶导数(如果同时为1,通常得不到想要的结果,想两个方向都处理的比较好 学习使用后面的算子)
**ksize**:Sobel算子的大小,可选择3、5、7,默认为3。
很多人疑问,Sobel算子的卷积核这几个值是怎么来的呢?事实上,并没有规定,你可以用你自己的。比如,最初只利用邻域间的原始差值来检测边缘的Prewitt算子:
Prewitt-X: Prewitt-Y:
[-1 0 +1] [-1 -1 -1]
[-1 0 +1] [ 0 0 0]
[-1 0 +1] [+1 +1 +1]还有比Sobel更好用的Scharr算子,大家可以了解下:
Scharr-X: Scharr-Y:
[-3 0 +3] [-3 -10 -3]
[-10 0 +10] [ 0 0 0]
[-3 0 +3] [+3 +10 +3]案例:
import cv2 as cv
import numpy as np
#读图
shu = cv.imread("D:\OpenCV_notes\day04\images\\shudu.png",cv.IMREAD_GRAYSCALE)
cv.imshow("shudu",shu)
#sobel
# dx=1,dy=0 水平方向上差分 提取垂直边缘
dst=cv.Sobel(shu,-1,1,0,ksize=3)
cv.imshow("sobel",dst)
# dx=0 dy=1 垂直方向上差分 提取水平边缘
dst1=cv.Sobel(shu,-1,0,1,ksize=3)
cv.imshow("sobel1",dst1)
cv.waitKey(0)
cv.destroyAllWindows()原图:

sobel水平差分后--sobel:

sobel垂直差分后--sobel1:
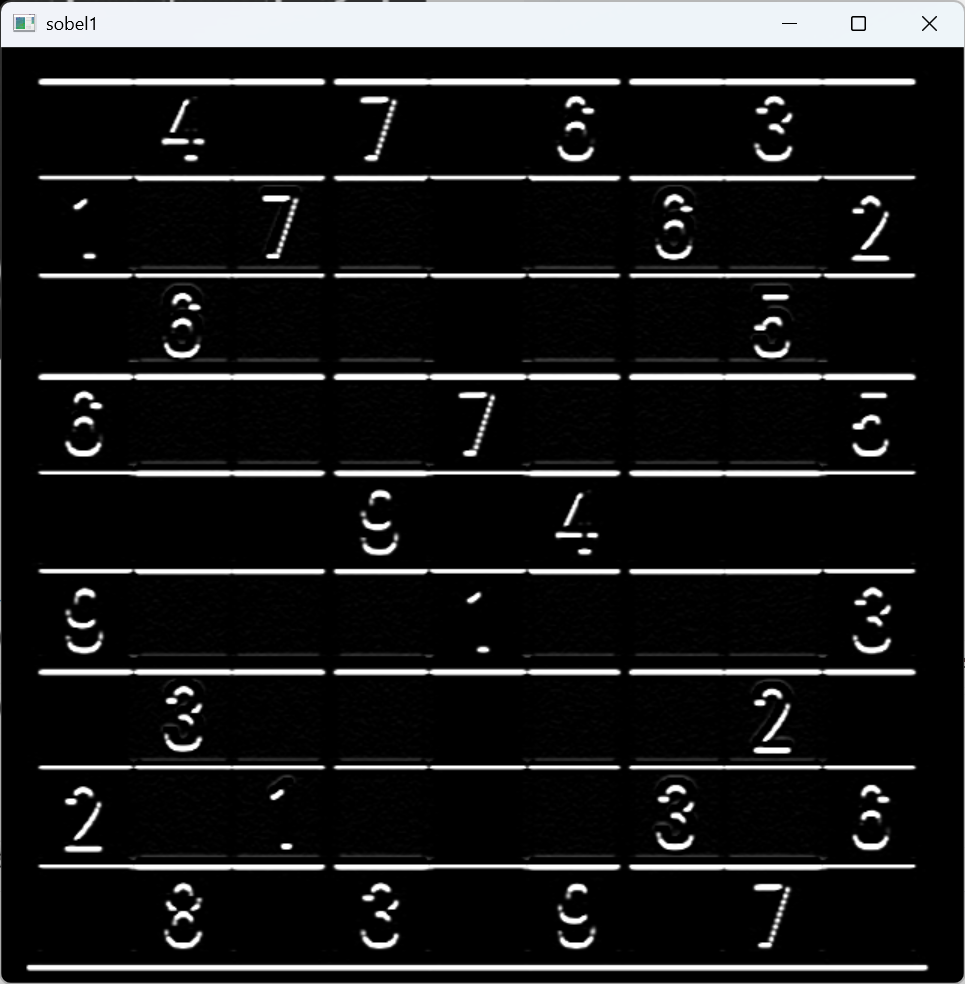
3.2 Laplacian算子
高数中用一阶导数求极值,在这些极值的地方,二阶导数为0,所以也可以通过求二阶导
计算梯度:
一维的一阶和二阶差分公式分别为:
提取前面的系数,那么一维的Laplacian滤波核是:
而对于二维函数f(x,y),两个方向的二阶差分分别是:
合在一起就是:
同样提取前面的系数,那么二维的Laplacian滤波核就是:
这就是Laplacian算子的图像卷积模板,有些资料中在此基础上考虑斜对角情况,将卷积核拓展为:





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1282
1282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








