代码随想录打卡Day2

原创已于 2024-10-18 04:46:04 修改 · 224 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #leetcode #线性代数

于 2024-10-17 14:03:19 首次发布

代码随想录专栏收录该内容

20 篇文章

订阅专栏

day02 数组

1 长度最小的子数组

介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入暴力解法的怪圈。

所以只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。

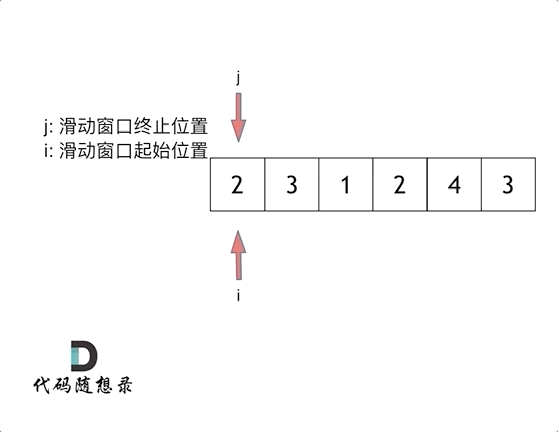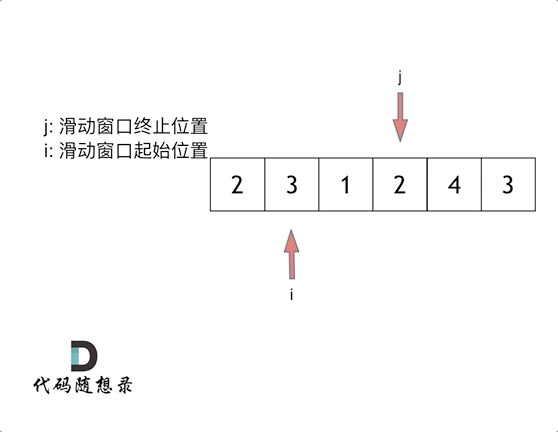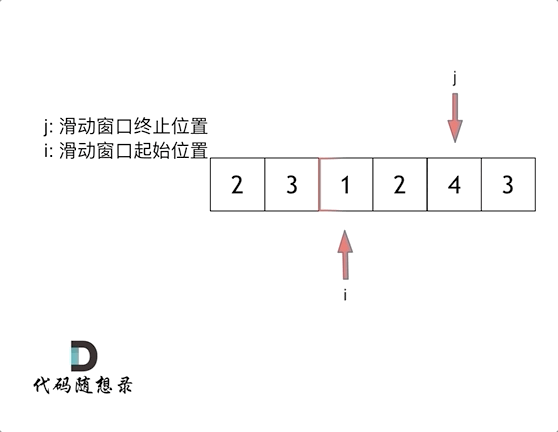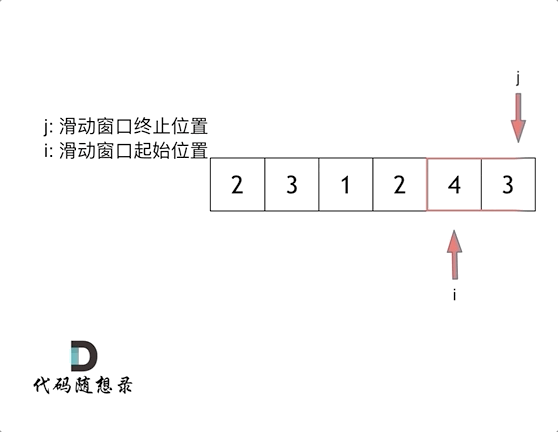
那么问题来了，滑动窗口的起始位置如何移动呢？

这里还是以题目中的示例来举例，s=7，数组是 2，3，1，2，4，3，来看一下查找的过程：

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0, right = 0, sum = 0, minLen = Integer.MAX_VALUE;

        while (right < nums.length) {
            sum += nums[right];
            while (sum >= target) {
                minLen = Math.min(minLen, right - left + 1);
                sum -= nums[left];
                left++;
            }
            right++;
        }
        return minLen == Integer.MAX_VALUE ? 0 : minLen;

    }
}
//leetcode submit region end(Prohibit modification and deletion)

2 螺旋数组59

package com.jiangxun.leetcode.editor.cn;//<p>给你一个正整数&nbsp;<code>n</code> ，生成一个包含 <code>1</code> 到&nbsp;<code>n<sup>2</sup></code>&nbsp;所有元素，且元素按顺时针顺序螺旋排列的&nbsp;<code>n x n</code> 正方形矩阵 <code>matrix</code> 。</p>
//
//<p>&nbsp;</p>
//
//<p><strong>示例 1：</strong></p> 
//<img alt="" src="https://assets.leetcode.com/uploads/2020/11/13/spiraln.jpg" style="width: 242px; height: 242px;" /> 
//<pre>
//<strong>输入：</strong>n = 3
//<strong>输出：</strong>[[1,2,3],[8,9,4],[7,6,5]]
//</pre>
//
//<p><strong>示例 2：</strong></p>
//
//<pre>
//<strong>输入：</strong>n = 1
//<strong>输出：</strong>[[1]]
//</pre>
//
//<p>&nbsp;</p>
//
//<p><strong>提示：</strong></p>
//
//<ul> 
// <li><code>1 &lt;= n &lt;= 20</code></li> 
//</ul>
//
//<div><div>Related Topics</div><div><li>数组</li><li>矩阵</li><li>模拟</li></div></div><br><div><li>👍 1340</li><li>👎 0</li></div>

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        //从1开始放数字
        int number = 1;
        //循环次数count
        int count = 1;
        //起点（x，y）,i是行，j是列
        int startX = 0;
        int startY = 0;
        int i=1;
        int j=1;
        //初始化偏移值设为 1，固定某一循环，每一次填充数量
        int offset = 1;

        /**
         * 3*3的矩阵
         * 第一次填充上部 1 2，第二次填充右侧 3 4 左闭右开
         * 第三次填充下部 5 6，第四次填充左部 7 8
         * （以此循环）填充 9
         */
        while (count <= n / 2) {
            //上
            for (j = startY; j < n - offset; j++) {
                nums[i][j] = number++;
            }
            //右
            for (i = startX; i < n - offset; i++) {
                nums[i][j] = number++;
            }
            //下
            for(; j > startY; j--){
                nums[i][j] = number++;
            }
            //左
            for(; i > startX; i--){
                nums[i][j] = number++;
            }
            //更新起点
            startX++;
            startY++;
            //更新偏移值
            offset++;
            //更新循环次数
            count++;

        }
        //如果n是奇数，单独处理中间数字
        if(n % 2 == 1){
            nums[startX][startY] = number;
        }
        return nums;
    }
}
//leetcode submit region end(Prohibit modification and deletion)

package com.jiangxun.leetcode.editor.cn;//<p>给你一个正整数&nbsp;<code>n</code> ，生成一个包含 <code>1</code> 到&nbsp;<code>n<sup>2</sup></code>&nbsp;所有元素，且元素按顺时针顺序螺旋排列的&nbsp;<code>n x n</code> 正方形矩阵 <code>matrix</code> 。</p>
//
//<p>&nbsp;</p>
//
//<p><strong>示例 1：</strong></p> 
//<img alt="" src="https://assets.leetcode.com/uploads/2020/11/13/spiraln.jpg" style="width: 242px; height: 242px;" /> 
//<pre>
//<strong>输入：</strong>n = 3
//<strong>输出：</strong>[[1,2,3],[8,9,4],[7,6,5]]
//</pre>
//
//<p><strong>示例 2：</strong></p>
//
//<pre>
//<strong>输入：</strong>n = 1
//<strong>输出：</strong>[[1]]
//</pre>
//
//<p>&nbsp;</p>
//
//<p><strong>提示：</strong></p>
//
//<ul> 
// <li><code>1 &lt;= n &lt;= 20</code></li> 
//</ul>
//
//<div><div>Related Topics</div><div><li>数组</li><li>矩阵</li><li>模拟</li></div></div><br><div><li>👍 1340</li><li>👎 0</li></div>

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        //从1开始放数字
        int number = 1;
        //循环次数count
        int count = 1;
        //起点（x，y）,i是行，j是列
        int startX = 0;
        int startY = 0;
        int i=1;
        int j=1;
        //初始化偏移值设为 1，固定某一循环，每一次填充数量
        int offset = 1;

        /**
         * 3*3的矩阵
         * 第一次填充上部 1 2，第二次填充右侧 3 4 左闭右开
         * 第三次填充下部 5 6，第四次填充左部 7 8
         * （以此循环）填充 9
         */
        while (count <= n / 2) {
            //上
            for (j = startY; j < n - offset; j++) {
                i=startX;
                nums[i][j] = number++;
            }
            //右
            for (i = startX; i < n - offset; i++) {
                nums[i][j] = number++;
            }
            //下
            for(; j > startY; j--){
                nums[i][j] = number++;
            }
            //左
            for(; i > startX; i--){
                nums[i][j] = number++;
            }
            //更新起点
            startX++;
            startY++;
            //更新偏移值
            offset++;
            //更新循环次数
            count++;

        }
        //如果n是奇数，单独处理中间数字
        if(n % 2 == 1){
            nums[startX][startY] = number;
        }
        return nums;
    }
}
//leetcode submit region end(Prohibit modification and deletion)

3 区间和
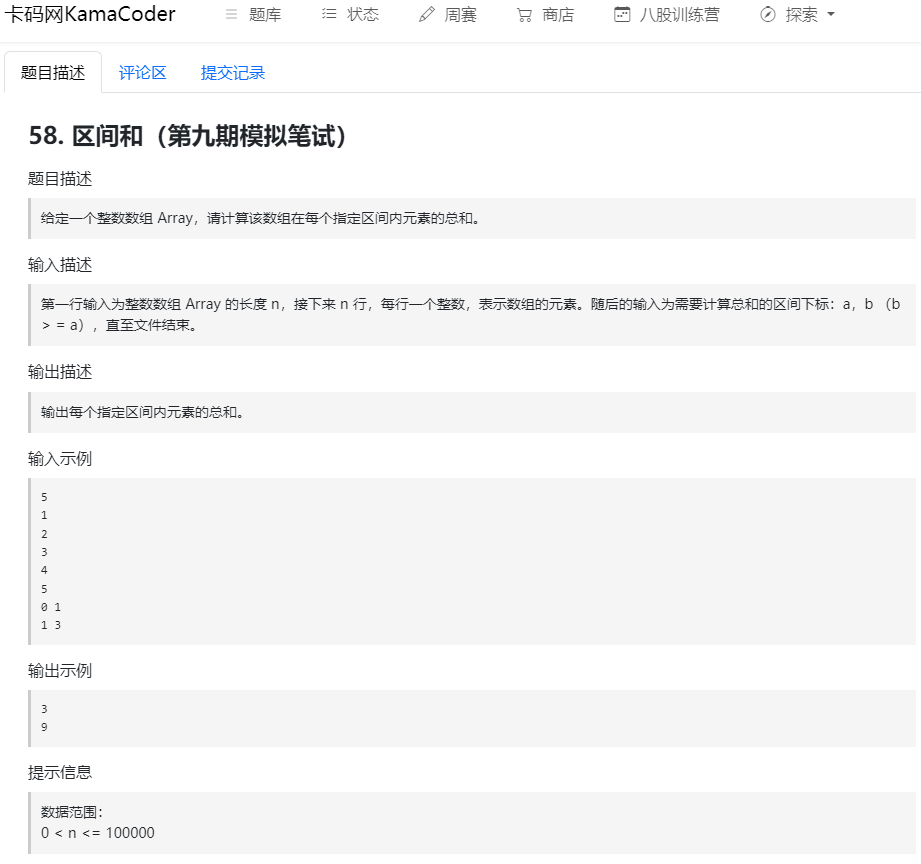
在这里插入图片描述

package com.jiangxun.array;

import java.util.Scanner;

public class PrefixSum {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int[] vec = new int[n];
        int[] p = new int[n];

        int presum = 0;
        for (int i = 0; i < n; i++) {
            vec[i] = scanner.nextInt();
            presum += vec[i];
            p[i] = presum;
        }

        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();

            int sum;
            if (a == 0) {
                sum = p[b];
            } else {
                sum = p[b] - p[a - 1];
            }
            System.out.println(sum);
        }
        scanner.close();
    }
}

开发商购买土地

【题目描述】

在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。

为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。

注意：区块不可再分。

【输入描述】

第一行输入两个正整数，代表 n 和 m。

接下来的 n 行，每行输出 m 个正整数。

输出描述

请输出一个整数，代表两个子区域内土地总价值之间的最小差距。

【输入示例】

3 3 1 2 3 2 1 3 1 2 3

【输出示例】

【提示信息】

如果将区域按照如下方式划分：

1 2 | 3 2 1 | 3 1 2 | 3

两个子区域内土地总价值之间的最小差距可以达到 0。

【数据范围】：

1 <= n, m <= 100；
n 和 m 不同时为 1。
#思路
看到本题，大家如果想暴力求解，应该是 n^3 的时间复杂度，

一个 for 枚举分割线，嵌套两个for 去累加区间里的和。

如果本题要求任何两个行（或者列）之间的数值总和，大家在0058.区间和的基础上应该知道怎么求。

就是前缀和的思路，先统计好，前n行的和 q[n]，如果要求矩阵 a行到 b行之间的总和，那么就 q[b] - q[a - 1]就好。

至于为什么是 a - 1，大家去看 0058.区间和的分析，使用前缀和要注意区间左右边的开闭情况。

本题也可以使用前缀和的思路来求解，先将行方向，和列方向的和求出来，这样可以方便知道划分的两个区间的和。

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int sum = 0;
        int[][] vec = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                vec[i][j] = scanner.nextInt();
                sum += vec[i][j];
            }
        }

        // 统计横向
        int[] horizontal = new int[n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                horizontal[i] += vec[i][j];
            }
        }

        // 统计纵向
        int[] vertical = new int[m];
        for (int j = 0; j < m; j++) {
            for (int i = 0; i < n; i++) {
                vertical[j] += vec[i][j];
            }
        }

        int result = Integer.MAX_VALUE;
        int horizontalCut = 0;
        for (int i = 0; i < n; i++) {
            horizontalCut += horizontal[i];
            result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
        }

        int verticalCut = 0;
        for (int j = 0; j < m; j++) {
            verticalCut += vertical[j];
            result = Math.min(result, Math.abs(sum - 2 * verticalCut));
        }

        System.out.println(result);
        scanner.close();
    }
}