python 基础知识点（蓝桥杯python科目个人复习计划54）

今日复习内容：做题

例题1：可凑成的最大花束数

问题描述：

情人节到了，妮妮学姐的追求者实在是太多了，她一共有n个追求者，第i个追求者送了ai朵颜色相同的花。每个追求者赠送的花朵颜色都不同。为了卖掉这些花并将所得款项捐赠给希望小学，妮妮学姐决定将k朵颜色不同的花打包成一个花束。请问她最多可以打包成多少个花束？

输入格式：

第一行输入两个整数n和k，分别表示妮妮学姐的追求者数量和打包需要的花朵数；

第二行输入n个整数ai，表示每个追求者赠送的花朵数量。

数据范围保证：1 <= n,k <= 2 * 10^5，1 <= ai <= 10^9

输出格式：

输出一个整数表示妮妮学姐最多可以打包成多少个花束。

参考答案：

n,k = map(int,input().split())
aa = list(map(int,input().split()))
def check(x):
    res = 0
    for i in range(n):
        res += min(aa[i],x)
    return res >= x * k
l = 0
r = 2 * 10 ** 14
ans = 0
while l <= r:
    mid = (l + r) // 2
    if check(mid):
        ans = mid
        l = mid + 1
    else:
        r = mid - 1
print(ans)

运行结果：

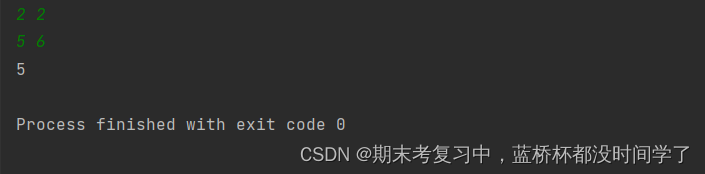
以下是我对此题的理解：

如果我们能够确定一个大小x，使得存在解满足打包k朵不同颜色花束的要求，那么我们可以不断尝试增大x，直到找到最大的满足要求的大小。

当我们面对这种问题时，我们首先要理解题目的要求。在这个问题中，妮妮学姐希望将她收到的花束打包成尽可能多的花束，每个花束中包含不同颜色的花朵，而且每个花束的数量为k。

首先，我们可以观察到，如果我们能够打包出k个花束。那么每个花束至少应该包括k朵不同颜色的花，否则，无法满足题目要求。

我们可以考虑通过二分查找方法来确定能够满足打包k朵不同颜色花束的最大花束大小x。这样，我们可以通过检查每个追求者赠送的花朵数量，统计出最大的花束大小。

具体来说，我们首先设定一个初始的二分查找范围，比如从0到一个很大的数，然后，我们不断地取中间值，检查是否存在大小为x的花束满足打包k朵不同颜色花束的要求。如果满足条件，我们将左边界移动到中间值的右侧，如果不满足条件，我们将右边界移动到中间值的左侧。通过这样的迭代过程，最终我们可以找到满足条件的最大的花束大小。

n,k = map(int,input().split())

这一行从输入中读取两个整数n和k，分别表示追求者数量和花束大小

aa = list(map(int,input().split()))

这一行从输入中读取n个整数，表示每个追求者送来的花束数量，并将它们储存在列表aa中

def check(x):

这一行定义了一个名为check的函数，该函数接受一个参数x，用于检查是否存在大小为x的花束满足要求

res = 0

初始化一个变量res，用于记录当前花束总数

for i in range(n)：

对于每个追求者，进行下列操作

res += min(aa[i],x):

将当前追求者送来的花束数量与x中较小的数相加，表示将当前追求者的花束数量按照要求打包成花束，然后将结果累加到res中。

return res >= x * k

最后，检查是否满足打包k朵不同颜色花束的条件，即检查res是否大于或等于x * k。如果是，则返回True，表示存在大小为x的花束满足要求；否则，返回False。

l = 0

初始化二分查找的左边界为0

r = 2 * 10 ** 14

初始化二分查找的右边界r为一个足够大的数，即2乘以10的14次方，这是因为花束数量的范围可能很大

ans = 0

初始化一个变量ans，用于记录最终找到的满足条件的花束大小

while l <= r:

开始二分查找的循环，当左边界小于等于右边界时执行

mid = (l + r) // 2

计算当前的中间值mid，用于确定下一步的查找范围

if check(mid):

调用check函数检查是否存在大小为mid的花束满足大小

l = mid + 1

将左边界移到中间值的右侧，继续查找更大的满足条件的花束大小

else:

如果不满足条件

r = mid - 1

将右边界移动到中间值的左边，缩小查找范围

print(ans)

输出答案

---

例题2：最大通过数

问题描述：

洛洛和晶晶计划一起挑战峡谷深渊，这个深渊有两个入口，分别为左边和右边。左边的入口有n个关卡，第i个关卡需要消耗ai块能源紫水晶。右边的入口有m个关卡，第i个关卡需要消耗bi块能源紫水晶。为了挑战下一个关卡，两个入口的关卡必须按顺序通过。

洛洛决定选择左边的入口，而晶晶决定选择右边的入口。两人总共只携带了k块能源紫水晶。他们不确定如何分配能源才能使得通过的关卡数之和最大。你需要帮助他们求出通过的关卡之数的最大值。请注意，你无需给出具体的能源分配方案，只需要计算可以达到的最大关卡数之和。

输入格式：

第一行输入3个整数n，m，k；

第二行输入n个整数ai；

第3行输入m个整数bi；

数据范围保证：1 <= n,m <= 2 * 10^5，1 <= ai,bi,k <= 10^9

输出格式：

输出一个整数，表示两人通过的关卡数之和最大值。

参考答案：

from bisect import *
n,m,k = map(int,input().split())
a = list(map(int,input().split()))
b = list(map(int,input().split()))
aa = [0]
bb = [0]
for i in range(n):
    aa.append(aa[-1] + a[i])
for j in range(m):
    bb.append(bb[-1] + b[j])
ans = 0
for i in range(0,n + 1):
    if aa[i] > k:
        break
    res = k - aa[i]
    ind = bisect_right(bb,res)
    ans = max(ans,i + ind - 1)
print(ans)

运行结果：

 

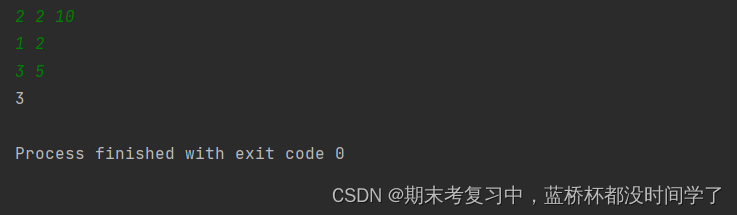
以下是我对此题的理解：

这道题我用的是贪心算法 + 二分查找

1.前缀和计算

我们首先计算出左边入口和右边入口的紫水晶消耗前缀和数组。这些前缀和数组分别表示从第一个关卡到当前关卡所需的紫水晶数总和。

对于左边入口，我们将每个关卡消耗的紫水晶数累加起来，得到左边入口的前缀和数组；

对于右边入口，同样地，我们将每个关卡消耗的紫水晶数累加起来，得到右边入口的前缀和数组；

2.遍历左边关卡入口

我们遍历左边入口的每个关卡，并计算洛洛通过当前关卡所消耗的紫水晶数量。

如果洛洛通过当前关卡所消耗的紫水晶数量超过了携带的紫水晶数量k，则表示洛洛无法通过后续关卡，因此我们推出循环

3.二分查找右边入口关卡

对于每个洛洛通过的关卡，我们需要在右边入口中找到满足晶晶所需紫水晶数量的最大关卡数

我们利用二分查找在右边入口的前缀和数组中找到满足晶晶所需紫水晶数量的最大关卡数

4.更新关卡数

对于每个洛洛通过的关卡，我们更新答案为左边入口通过的关卡数和右边入口通过的关卡数之和的最大值。

5.输出答案

最终，我们输出通过的关卡数之和的最大值

from bisect import *

导入bisect模块，用于二分查找

n,m,k = map(int,input().split())

从输入中读取3个整数n，m，k，分别表示左边入口的关卡数，右边入口的关卡数和两人携带的能源紫水晶数量

a = list(map(int,input().split()))

从输入中读取n个整数，表示左边入口每个关卡消耗的能源紫水晶数量，并将它们储存在列表a中

b = list(map(int,input().split()))

从输入中读取m个整数，表示左边入口每个关卡消耗的能源紫水晶数量，并将它们储存在列表b中

aa = [0]

初始化一个列表aa，用于存储左边列表前缀和，初始值为0，表示从第一个关卡开始消耗的紫水晶数量总和为0

bb = [0] 

初始化一个列表bb，用于存储右边列表前缀和，初始值为0，表示从第一个关卡开始消耗的紫水晶数量总和为0

for i in range(n)

对于左边入口的每个关卡，执行以下操作

aa.append(aa[-1] + a[i])

将当前关卡消耗的紫水晶数量与前一个关卡的紫水晶数量总和相加，并将结果添加到aa列表中，表示从第一个关卡到当前关卡所需的所需的紫水晶数量总和

for j in range(m):bb.append(bb[-1] + b[j])

if aa[i] > k:break

检查洛洛通过当前关卡时消耗的紫水晶数量是否超过了携带的紫水晶数量k，如果超过，则跳出循环，因为后续关卡无法通过。

res = k - aa[i]

计算晶晶还剩余的紫水晶数量

ind = bisect_right(bb,res)

利用二分查找在右边入口中找到满足晶晶所需所需紫水晶数量的最大关卡数，bisect_right函数返回的索引值表示第一个大于给定值元素的位置（这个位置不符合条件，后面要减去）

ans = max(ans,i + ind - 1)

更新ans为当前通过的关卡数之和的最大值，即左边入口通过的关卡数i和右边入口通过的关卡数ind - 1的和

最后输出答案。

---

例题3：妮妮的月饼工厂

问题描述：

中秋节即将来临，妮妮在小镇上开了一家月饼厂，她手中有N块原材料，这些原材料宽度相同，但高度不同。妮妮可以选择任意一块原材料进行切割，切割后的两块原材料高度必须为整数，切割只能沿水平线进行，所以切割后的两块原材料宽度与切割前相同。

妮妮的目标是用这些原材料制作出k个高度完全相同的月饼。请问，这k个月饼的最高高度能是多少？

输入格式：

第一行包含两个整数N和K， 1 <= N <= 10^5,1 <= K <= 10^9

第二行包含N个整数，代表N块原材料的初始高度（初始是介于1到10^9的整数）

输出格式：

如果无法制作出高度完全相同的k个月饼，输出-1

否则，在第一行输出这k个月饼的最高高度

参考答案：

n,k = map(int,input().split())
li = list(map(int,input().split()))
def check(mid):
    ans = 0
    for i in range(n):
        ans += li[i] // mid
    return ans >= k
l = 1
r = int(1e9)
ans = 0
while l <= r:
    mid = (l + r) // 2
    if check(mid):
        ans = mid
        l = mid + 1
    else:
        r = mid - 1
if ans == 0:
    print(-1)
else:
    print(ans)

运行结果：

 

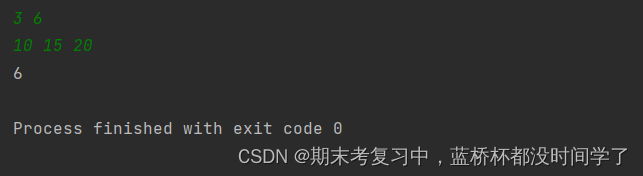
以下是我对此题的理解：

这个问题是一个典型的二分查找问题，通过二分法找到最大高度，使得可以制作出k个高度完全相同的月饼。

整体思路：

1.二分查找范围

因为月饼的高度范围在1到10^9之间，所以我们可以使用二分查找来找到复核人条件的最大高度，我们将搜索范围初始化为[1,10^9]

2.二分查找核心逻辑

在每一次循环中，我们计算出当前高度mid是否满足条件，即是否可以制作出至少k个高度为mid的月饼；我们定义了一个check函数，来检查是否可以制作出k个高度相同的月饼，如果可以，则返回True,否则返回False

3.更新搜索范围

如果当前高度mid可以制作出至少k个月饼，则将答案更新为当前高度mid，并将搜索范围调整为[mid + 1,r]，继续查找更大的高度；否则，将搜索范围调整为[l,mid - 1]，继续查找更小的高度。

4.输出结果

最终如果找到了符合条件的最大高度，则输出该高度作为答案；如果找不到，则输出-1。

---

例题4：基德的神秘冒险

问题描述：

基德是一个勇敢的冒险家，他正在一片神秘的森林中探险。这片森林被一种神秘的力量保护着，这种力量由一个特殊的神秘阵列控制，这个阵列由N块石碑组成，每块石碑上都刻有一个神秘的数Ai。在这个阵列中，任意3块不同的石碑，都会形成一个三石碑组（我们称之为“三重石”），而这个“三重石”的力量则是这三块石头上刻的数字中最小的那个。

基德需要掌握这个序列的力量，来对抗森林中的邪恶力量，他的朋友小新给了他一个神秘的水晶球，可以用来查询这个阵列的信息。每次查询，基德都需要提供一个数字k，然后水晶球就会显示出“三重石”中第k小的力量数值。

基德需要你的帮助来理解这个阵列的力量，你能帮助他吗？

输入描述：

第一行输入两个整数N和Q，其中N是石碑的数量，Q是基德此次查询的次数

第二行输入N个整数A1,A2,...,AN，分别代表每块石碑上的神秘数字

接下来Q行每次输入一个数，每个数是基德此次查询的k值。

数据范围保证：3 <= N <= 3 * 10^5,1 <= Q <= 3 * 10^5,-10^9 <= Ai <= 10^9,1 <= k <= C(3 N)

输出格式：

对于每次查询，你需要输出一个数字，代表“三重石”中第k小的力量数值。

参考答案：

from bisect import *
n,q = map(int,input().split())
aa = list(map(int,input().split()))
aa.sort()
pre = [0] * n
for i in range(n):
    pre[i] = (n - 1 - i) * (n - 2 - i) // 2
    if i > 0:
        pre[i] += pre[i - 1]
for i in range(q):
    qq = int(input())
    ind = bisect_left(pre,qq)
    print(aa[ind])

运行结果：

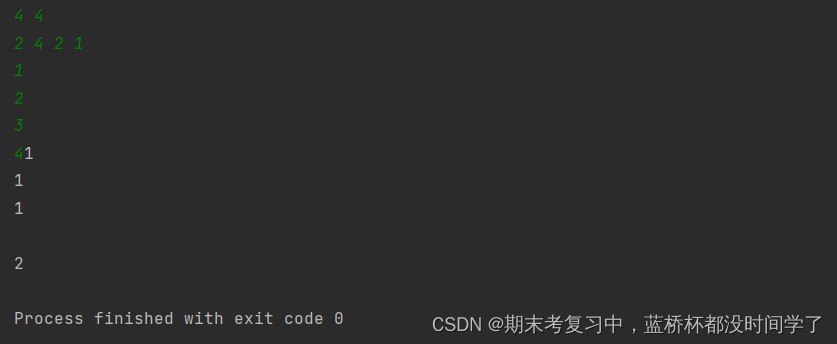
以下是我对此题的理解：

这个题的关键点是：

1.排序石碑神秘数值：将石碑上的神秘数值列表进行排序，以便后续的二分查找

2.计算前缀和：使用一个列表pre来存储每个位置的前缀和，表示当前位置的前面有多少个三重石。这是通过组合数的方式计算得到的。

3.查询过程

对于每次查询，输入一个数字qq，然后通过二分查找bisect_left找到第一个大于等于qq的位置；

输出对应位置的石碑上的神秘数值，这个位置即为满足条件的三重石中第qq小的力量数值。

总体思路是通过预先计算前缀和，然后通过二分查找来快速定位到查询的位置，最终输出对应位置的神秘数值。

from bisect import *:导入bisect模块，该模块提供了二分查找算法的实现

n,q = map(int,input().split())：输入石碑的数量n和查询的次数q

aa = list(map(int,input().split()))：输出每个石碑上的神秘数值列表，并将其存储在列表aa中

aa.sort()：对神秘数值列表进行排序，为后续的二分查找做准备

pre = [0] * n：创建一个长度为n的列表，用于存储每个位置的前缀和

for i in range(n)：循环遍历每个石碑的位置i

pre[i] = (n - i - 1) * (n - 2 - i) // 2：计算当前位置的前缀和

if i > 0:pre[i] += pre[i - 1]：如果不是第一个位置，累加前一个位置的前缀和

for i in range(q)：循环遍历每个查询

qq = int(input())：输入查询的数字qq

ind = bisect_left(pre,qq)：使用二分查找找到第一个大于等于qq的位置

print(aa[ind])：输出对应位置的石碑上的神秘数值

---

 OK，这篇就写到这里，下一篇继续！