python 基础知识点（蓝桥杯python科目个人复习计划40）

最新推荐文章于 2025-12-28 07:10:27 发布

原创最新推荐文章于 2025-12-28 07:10:27 发布 · 683 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#python #蓝桥杯 #开发语言

本文回顾了矩阵乘法和高斯消元的基本概念，并提供了Python实现的代码示例，包括矩阵乘法运算器和线性方程组求解，展示了在IT技术中解决实际问题的方法。

今日复习内容：矩阵乘法，高斯消元

哈哈，我来干回老本行，复习点儿数学类专业学的东西

因为电脑上制作费时间，所以我直接用我的《高等代数》和《数值分析》笔记。

一.矩阵乘法

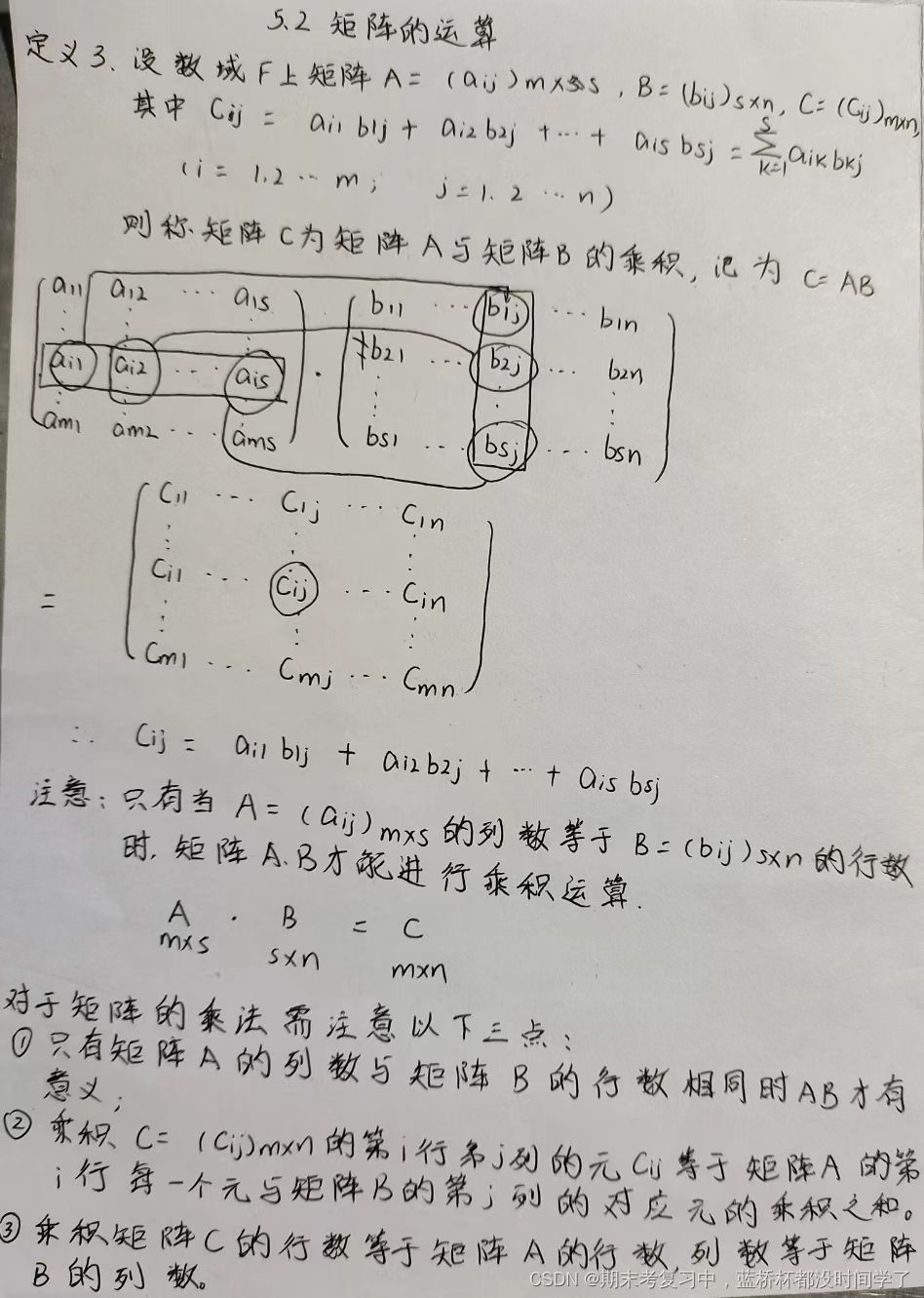
例题1：矩阵相乘

题目描述：

小明最近刚刚学习了矩阵乘法，但是他计算的速度太慢，于是他希望你能帮他写一个矩阵乘法的运算器。

输入描述：

输入的第一行包括三个正整数N,M,K，表示一个N行M列的矩阵乘以一个M行K列的矩阵。接下来N行，每行M个整数，表示第一个矩阵，接下来的M行，每个K个整数，表示第二个矩阵。

0 < N,M,K <= 100, 0 <= 矩阵中的每个整数 <=1000.

输出描述：

输出有N行，每行K个整数，表示矩阵乘法的结果。

参考答案：

def mul(A,B):
    N,M = len(A),len(A[0])
    _M,K = len(B),len(B[0])
    if M != _M:
        return False
    C = [[0] * K for i in range(N)]
    for i in range(N):
        for j in range(K):
            for k in range(M):
                C[i][j] += A[i][k] * B[k][j]
    return C

def read(A,n):
    for i in range(n):
        A.append(list(map(int,input().split())))

def output(A):
    for x in A:
        print(' '.join(map(str,x)))

A = []
B = []
N,M,K = map(int,input().split())
read(A,N)
read(B,M)
C = mul(A,B)
output(C)

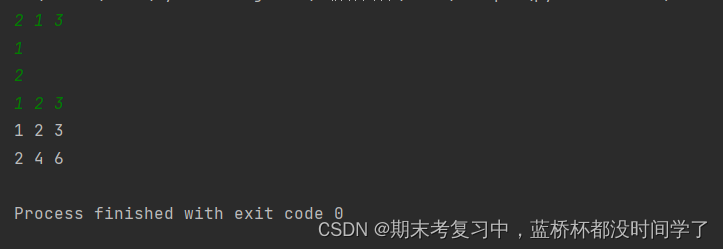
运行结果：

二.高斯消元

（这是我自己的实验报告，但是代码是Matlab写的，所以没有截下来）

例题2：n元一次线性方程组

（我去找了一个我的期末考题，写成了蓝桥杯题目的形式）

参考答案：

import numpy as np

def solve_linear_system(n, coefficients):
  A = np.array([equation[:-1] for equation in coefficients])
  b = np.array([equation[-1] for equation in coefficients])

  try:
    # 尝试解线性方程组
    solution = np.linalg.solve(A, b)
    return solution.round(2)
  except np.linalg.LinAlgError:
    # 如果出现LinAlgError，则说明无解
    return -1

# 示例输入
n = int(input())
coefficients = []
for _ in range(n):
  equation = list(map(float, input().split()))
  coefficients.append(equation)

# 求解线性方程组
solution = solve_linear_system(n, coefficients)

# 输出结果
if isinstance(solution, np.ndarray):
  for s in solution:
    print(s)
else:
  print(solution)

仅供参考，我虽然懂原理，但是我还是觉得有点难。

OK，这篇就写到这里，下次继续！