目录
一、什么是决策树
决策树是一种基于规则的方法, 它用一组嵌套的规则进行预测。 在树的每个决策节点处, 根据判断结果进入一个分支, 反复执行这种操作直到到达叶子节点,得到 预测 / 分类结果。
二、树形决策过程

决策树的节点分为两种类型:
- 决策节点。 在这些节点处需要进行判断以决定进入哪个分支。
- 叶子节点。 表示最终的决策结果。 对于分类问题, 叶子节点中存储的是类别标签。
三、训练算法
1、递归分裂过程
首先创建根节点, 然后递归地建立左子树和右子树。
假如训练样本集为 D, 训练算法的整体流程如下:
- 用样本集 D 建立跟节点, 找到一个判定条件, 为根节点设置判定规则,将样本集分裂成 D1 和 D2 两部分。
- 用样本集 D1 递归建立左子树。
- 用样本集 D2 递归建立右子树。
- 如果不能再进行分裂, 则把节点标记为叶子节点, 同时为它赋值。
2、寻找最佳分裂
最佳分裂即保证分裂之后的左右子树的样本尽可能纯, 即他们的样本尽可能属于不相交的类。
定义不纯度指标,当样本只属于某一类时指标最小, 当样本均匀地分布于所有类中时指标最大, 因此, 如果能找到一个分裂让指标最小, 这就是我们想要的最佳分裂。
2.1 阈值设定
假设特征分量是数值型的, 我们为每个特征分量设置一系列阈值, 分别用每个阈值计算样本集分裂后的不纯度, 不纯度值最小对应的分裂就是最佳分裂。 每次都选择当前条件下最好的分裂作为决策节点的分裂。
2.2 分类问题
前提:每个类出现的概率,
是第 i 类样本数,
为总样本数。
2.2.1 不纯度指标
熵不纯度

Gini 不纯度

误分类不纯度
![]()
2.2.2 分裂的不纯度
分裂规则训练样本分裂成左、 右两个子集, 分裂的目标是分裂后的两个子集都尽可能纯。
因此, 计算左、右子集的不纯度加权和作为分裂结果的不纯度, 以反映左右两边训练样本数的差异。

是左子集的不纯度,
是右子集的不纯度,
是总样本数,
是左子集的样本数,
是右子集的样本数。
2.3 回归问题
使用回归误差(即样本方差)来表示不纯度。
假设节点的训练样本集有 个样本
,
为特征向量,
为标签值,
是样本集
所有样本标签的均值。样本集
的回归误差定义为:

3、叶子节点的设定
如果不能继续分裂, 则将该节点设置为叶子节点。
- 分类问题(分类树),将叶子节点的值设置成本节点的训练样本集中出现概率最大的那个类;
- 回归问题(回归树), 叶子节点的值设置为本节点训练样本标签的均值。
4、 剪枝算法
如果决策树的结构过于复杂, 可能会导致过拟合问题。 此时需要对树进行剪枝, 消掉某些节点让它变得更简单。
剪枝算法的实现方案为计算出所有非叶子节点的 值之后, 剪掉
值最小的节点得到剪枝后的树, 然后重复这种操作。
4.1 预剪枝
在树的训练过程中通过停止分裂对树的规模进行限制,其中包括限定树的高度、 节点的训练样本数、 分裂纯度提升的最小值
4.2 后剪枝
先训练得到一棵完整的树, 然后通过某种规则消掉部分节点。
包括降低错误剪枝(Reduced-Error Pruning, REP) 、 悲观错误剪枝( Pesimistic-Error Pruning, PEP) 、 代价-复杂度剪枝(Cost-Complexity pruning, CCP) 等
CCP
代价是指剪枝后导致的错误率的变化值, 复杂度是指决策树的规模。
计算α
首先计算该决策树每个非叶子节点的 值,
值表示将整个子树剪掉之后用一个叶子节点代替, 相对于原来的子树错误率的增加值。该值越小, 剪枝之后树的预测效果与剪枝之前越接近。
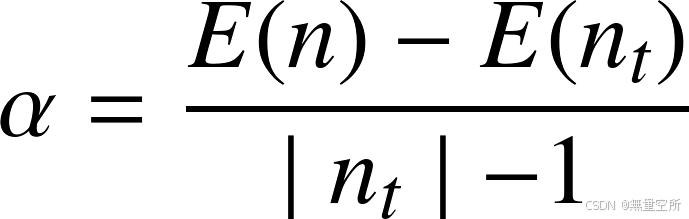
是节点 n 的错误率,
是以节点 n 为根的子树的错误率, 是该子树所有叶子节点的错误率之和,
是子树的叶子节点数量, 即复杂度。
计算E(n)
分类问题

是节点的总样本数,
是第 i 类样本数。
回归问题

四、代码
1、手动实现+预剪枝
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 定义节点类
class Node:
def __init__(self, feature_index=None, threshold=None, left=None, right=None, value=None):
self.feature_index = feature_index
self.threshold = threshold
self.left = left
self.right = right
self.value = value
# 定义决策树类
class DecisionTree:
def __init__(self, max_depth=None, min_samples_split=2):
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.root = None
# 计算基尼系数
def gini(self, y):
types, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
return 1 - np.sum(probabilities * probabilities)
# 计算基尼不纯度
def gini_impurity(self, y_left, y_right):
n = len(y_left) + len(y_right)
gini_left = self.gini(y_left)
gini_right = self.gini(y_right)
return (len(y_left) / n) * gini_left + (len(y_right) / n) * gini_right
# 选择最佳分裂特征和阈值
def find_best_split(self, X, y):
m, n = X.shape
best_gini = float('inf')
best_feature_index = None
best_threshold = None
for feature_index in range(n):
thresholds = np.unique(X[:, feature_index])
for threshold in thresholds:
y_left = y[X[:, feature_index] <= threshold]
y_right = y[X[:, feature_index] > threshold]
gini = self.gini_impurity(y_left, y_right)
if gini < best_gini:
best_gini = gini
best_feature_index = feature_index
best_threshold = threshold
return best_feature_index, best_threshold
# 构建决策树
def build_tree(self, X, y, depth=0):
unique, counts = np.unique(y, return_counts=True)
most_common = unique[np.argmax(counts)]
# 检查终止条件
if (self.max_depth is not None and depth >= self.max_depth) or len(y) < self.min_samples_split:
return Node(value=most_common)
# 寻找最佳分裂特征和阈值
best_feature_index, best_threshold = self.find_best_split(X, y)
# 分裂数据集
left_indices = X[:, best_feature_index] <= best_threshold
right_indices = X[:, best_feature_index] > best_threshold
left = self.build_tree(X[left_indices], y[left_indices], depth + 1)
right = self.build_tree(X[right_indices], y[right_indices], depth + 1)
return Node(feature_index=best_feature_index, threshold=best_threshold, left=left, right=right)
# 拟合模型
def fit(self, X, y):
self.root = self.build_tree(X, y)
# 预测
def predict(self, X):
return np.array([self.predict_tree(x, self.root) for x in X])
# 预测单个样本
def predict_tree(self, x, node):
if node.value is not None:
return node.value
if x[node.feature_index] <= node.threshold:
return self.predict_tree(x, node.left)
else:
return self.predict_tree(x, node.right)
# 测试代码
if __name__ == "__main__":
# 加载数据
iris = load_iris()
X, y = iris.data, iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 初始化并拟合模型
dt = DecisionTree(max_depth=5, min_samples_split=10)
dt.fit(X_train, y_train)
# 预测
y_pred = dt.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
2、手动实现+后剪枝
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 定义节点类
class Node:
def __init__(self, feature_index=None, threshold=None, left=None, right=None, value=None):
self.feature_index = feature_index
self.threshold = threshold
self.left = left
self.right = right
self.value = value
# 定义决策树类
class DecisionTree:
def __init__(self, ccp_alpha=0.0):
self.ccp_alpha = ccp_alpha
self.root = None
# 计算基尼系数
def gini(self, y):
types, counts = np.unique(y, return_counts=True)
probabilities = counts / len(y)
return 1 - np.sum(probabilities ** 2)
# 计算基尼不纯度
def gini_impurity(self, y_left, y_right):
n = len(y_left) + len(y_right)
gini_left = self.gini(y_left)
gini_right = self.gini(y_right)
return (len(y_left) / n) * gini_left + (len(y_right) / n) * gini_right
# 选择最佳分裂特征和阈值
def find_best_split(self, X, y):
m, n = X.shape
best_gini = float('inf')
best_feature_index = None
best_threshold = None
for feature_index in range(n):
thresholds = np.unique(X[:, feature_index])
for threshold in thresholds:
y_left = y[X[:, feature_index] <= threshold]
y_right = y[X[:, feature_index] > threshold]
gini = self.gini_impurity(y_left, y_right)
if gini < best_gini:
best_gini = gini
best_feature_index = feature_index
best_threshold = threshold
return best_feature_index, best_threshold
# 构建决策树
def build_tree(self, X, y):
unique, counts = np.unique(y, return_counts=True)
most_common = unique[np.argmax(counts)]
# 检查终止条件
if len(np.unique(y)) == 1:
return Node(value=most_common)
# 寻找最佳分裂特征和阈值
best_feature_index, best_threshold = self.find_best_split(X, y)
# 分裂数据集
left_indices = X[:, best_feature_index] <= best_threshold
right_indices = X[:, best_feature_index] > best_threshold
left = self.build_tree(X[left_indices], y[left_indices])
right = self.build_tree(X[right_indices], y[right_indices])
return Node(feature_index=best_feature_index, threshold=best_threshold, left=left, right=right, value=most_common)
# 后剪枝
def prune_tree(self, node, X, y):
if node.left is None and node.right is None:
return
error_rate = self.error_rate(y)
if node.left:
left_indices = X[:, node.feature_index] <= node.threshold
left_error, leaf = self.tree_error(node.left, X[left_indices], y[left_indices], 0)
if (error_rate - left_error)/leaf < self.ccp_alpha:
node.left = Node(value=node.value)
if node.right:
right_indices = X[:, node.feature_index] > node.threshold
right_error, leaf = self.tree_error(node.right, X[right_indices], y[right_indices], 0)
if (error_rate - right_error)/leaf < self.ccp_alpha:
node.right = Node(value=node.value)
if node.left:
self.prune_tree(node.left, X, y)
if node.right:
self.prune_tree(node.right, X, y)
# 计算节点错误率
def error_rate(self, y):
unique, counts = np.unique(y, return_counts=True)
most_common = counts[np.argmax(counts)]
return 1 - most_common / len(y)
# 计算子树的错误率
def tree_error(self, node, X, y, leaf):
error_rate = 0
if node.left is None and node.right is None:
error_rate += self.error_rate(y)
leaf += 1
else:
if node.left:
left_indices = X[:, node.feature_index] <= node.threshold
error, leaf = self.tree_error(node.left, X[left_indices], y[left_indices], leaf)
error_rate += error
if node.right:
right_indices = X[:, node.feature_index] > node.threshold
error, leaf = self.tree_error(node.right, X[right_indices], y[right_indices], leaf)
error_rate += error
return error_rate, leaf
# 拟合模型
def fit(self, X, y):
self.root = self.build_tree(X, y)
self.look(self.root)
self.prune_tree(self.root, X, y)
print("**************")
self.look(self.root)
def look(self, node):
if node.left is not None and node.right is not None:
print("feature_index:{},threshold:{}".format(node.feature_index, node.threshold))
if node.left is not None:
self.look(node.left)
if node.right is not None:
self.look(node.right)
# 预测
def predict(self, X):
return np.array([self.predict_tree(x, self.root) for x in X])
# 预测单个样本
def predict_tree(self, x, node):
if node.left is None and node.right is None:
return node.value
if x[node.feature_index] <= node.threshold:
return self.predict_tree(x, node.left)
else:
return self.predict_tree(x, node.right)
# 测试代码
if __name__ == "__main__":
# 加载数据
iris = load_iris()
X, y = iris.data, iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=41)
# 初始化并拟合模型
dt = DecisionTree(ccp_alpha=0.01)
dt.fit(X_train, y_train)
# 预测
y_pred = dt.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
3、sklearn库实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree
from sklearn.metrics import accuracy_score
from matplotlib import pyplot as plt
iris = load_iris()
X = iris.data
y = iris.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 决策节点的样本数不能少于5
dc_tree = tree.DecisionTreeClassifier(criterion='entropy', max_depth=4, min_samples_leaf=5)
dc_tree.fit(X_train, y_train)
y_predict = dc_tree.predict(X_test)
accuracy = accuracy_score(y_test, y_predict)
print(accuracy)
fig = plt.figure()
tree.plot_tree(dc_tree, filled=True,
feature_names=['sepal length', 'sepal width', 'petal length', 'petal width'],
class_names=['Setosa', 'Versicolour', 'Virginica'])
plt.show()





















 1917
1917

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








