题解：P10500 Rainbow的信号

思路来源：《算法竞赛进阶指南》–lyd

题意解析

给你一个数列 $A$，从中等概率地选取一个左端点为 $l$，右端点为 $r$ 的区间，得到的数组成一个新数列 $P$。

求数列 $P$ 的 xor，and，or和的期望。

题目分析

我们都知道，期望这东西实质上就是带权平均值，权重是这个值出现的概率（不了解的同学可以自行百度期望的概念）。所以我们需要从概率下手。

概率

考虑 $l=r$ 的情况，显然从 $1\sim n$ 中同时选到 $l,r$ 的概率为

$$\frac{1}{n}\times \frac{1}{n}=\frac{1}{n^2}$$

（根据乘法原理，同时选到 $l,r$ 的概率就是，选到 $l$ 的概率乘以选到 $r$ 的概率）。

考虑 $l\ne r$ 的情况，显然从 $1\sim n$ 中选到 $l,r$ 的概率为

$$\frac{1}{n}\times \frac{1}{n}+\frac{1}{n}\times \frac{1}{n}=\frac{2}{n^2}$$

有的同学就问了，为什么这里要乘以 $2$？因为题目中说到

如果 $l>r$，则交换 $l,r$。

所以这里相当于两种情况归并到一种，概率就要乘以 $2$ 了。

那这个时候我们就把概率搞清楚了，该搞期望了。

期望

期望无非就是在概率的基础上乘以值，这里才用逐位操作的方法，即把所有 $A_i$ 拆分成二进制的形式。

这样，我们可以一层一层地算，假设当前枚举到了第 $k$ 位，对于每个 $A_i$ 的第 $k$ 位，我们用 $B_i$ 表示。

为什么这样做？因为位运算不进位，不同位都是独立的，互不影响；这题又涉及位运算，相同位是可以影响的。所以我们不妨拆开每个数来算。

这么一来，根据期望是线性的，累加每一位的贡献即可。

先考虑 $l=r$，因为每一位的实际意义是整数的第 $k$ 位，所以当 $B_i=1$ 时，对答案的贡献是

$$2^k\times \frac{1}{n^2}$$

计算过程中顺手加上即可。

再考虑 $l\ne r$，我们分 and，or，xor三部分，从易到难来讲。

and

根据 and的定义，不难发现，只要区间内有一个 $0$，最后得到的这一位就是 $0$，期望也是 $0$，所以考虑 $B_r=1$ 的情况即可。

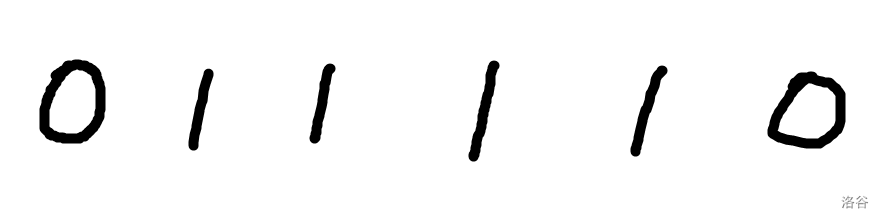
以这个为例，显然两个 $0$ 中间夹的区间只有 $(2,3)$，$(2,4)$，$(2,5)$ 对答案有贡献，并且贡献值一样。

设 $last[0]$ 表示上一个最近的 $0$ 的位置，所以整个下来的 and期望值为

$$2^k\times ((r-1)-(last[0]+1)+1)\times \frac{2}{n^2}$$

其中 $2^k$ 的意义同上所述，$(r-1)-(last[0]+1)+1$ 是满足结果为 $1$ 的区间总数 $sum-1$，$-1$ 是为了忽略掉 $l=r$ 的情况，最后乘以概率 $\frac{2}{n^2}$ 就有上述式子了。

or

根据 or的定义，如果区间内有 $1$ 最后就是 $1$ 了，所以分开讨论。

考虑 $B_r=1$ 的情况，无论 $l$ 怎么取，都对答案有贡献，所以同 and，有贡献为

$$2^k\times (r-1)\times \frac{2}{n^2}$$

考虑 $B_r\ne 1$，那么只有 $l\sim r$ 有至少一个 $1$，结果才有贡献。

设 $last[1]$ 表示上一个最近的 $1$ 的出现位置，那么只要 $l\in [1,last[1]]$，结果就有贡献。

这里 $l$ 是有 $1\sim last[1]$ 一共 $last[1]$ 种选择，贡献就为

$$2^k\times last[1]\times \frac{2}{n^2}$$

xor

根据 xor的定义，遇到 $0$ 时结果不变，遇到 $1$ 时取反，所以我们以 $1$ 为界来分割，每个割出来的部分 xor和都是 $1$。

我们定义两个变量 $c_1,c_2$，分别记录奇数段和偶数段的长度，不难发现 $B_r=0$ 时，每次 xor到偶数段时结果为 $1$，所以拿偶数段总长计算即可，期望为

$$2^k\times c_2\times \frac{2}{n^2}$$

同理，$B_r=1$ 时为

$$2^k\times c_1\times \frac{2}{n^2}$$

并且遇见 $1$ 时，要将 $c_1,c_2$ 互换，因为此时分出来了新段，奇数偶数段互换。

综上

将所有期望分情况计算累加，最后保留三位小数输出即可。

代码实现

需要注意的是，因为涉及 *运算，不要忘记开 long long！

#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
inline long long read()
{
    char c = 0; int x = 0; bool f = 0;
    while (!isdigit(c)) f = c == '-', c = getchar();
    while (isdigit(c)) x = x * 10 + c - 48, c = getchar();
    return f ? -x : x;
}
long long a[100010], n, last[2], c1, c2;//别忘了开long long
double ansxor, ansor, ansand;
int main()
{
    n = read();
    for (register int i = 1; i <= n; ++i)
        a[i] = read();
    for (register int k = 0; k <= 30; ++k)
    {
        last[0] = last[1] = c1 = c2 = 0;
        for (register int i = 1; i <= n; ++i)
        {
            int now = (a[i] >> k) & 1;
            double temp = 1.0 * (1 << k) / (n * n);
            if (now)
            {
                ansand += temp + 2.0 * temp * (i - last[0] - 1);
                ansor += temp + 2.0 * temp * (i - 1);
                ansxor += temp + 2.0 * temp * c1;
                ++c1;
                swap(c1, c2);
            }
            else
            {
                ansor += 2.0 * temp * last[1];
                ansxor += 2.0 * temp * c2;
                ++c1;
            }
            last[now] = i;
        }
    }
    printf("%.3lf %.3lf %.3lf", ansxor, ansand, ansor);
    return 0;
}