数据结构——查找（二、顺序查找、折半查找和分块查找）

Nanmi(发奋图强版)

已于 2025-08-03 23:54:53 修改

阅读量813

点赞数 28

CC 4.0 BY-SA版权

分类专栏：数据结构文章标签：算法数据结构

于 2025-08-02 00:18:33 首次发布

本文链接：https://blog.youkuaiyun.com/m0_65656149/article/details/149842043

数据结构专栏收录该内容

11 篇文章

订阅专栏

一、顺序查找

顺序查找也称线性查找，对线性表和链表都适用。

顺序查找分为一般的无序线性表的顺序查找和对按关键字有序的线性表的顺序查找（判定树）

对链表只能进行顺序查找

顺序查找都可以使用链表和顺序表，都可以有序或无序

1、一般线性表的顺序查找

typedef int ElemType;
// 定义结构体SSTable，表示顺序表
typedef struct {
    ElemType* elem;        // 动态数组基址 
    int TableLen;         // 表的长度
} SSTable;

// (哨兵方法） 函数Search_Seq1在顺序表S中顺序查找关键字等于key的数据元素
int Search_Seq1(SSTable S, ElemType key) {
	int i=0;
    S.elem[0] = key;  // 哨兵 
    for (i = S.TableLen; S.elem[i]!= key; --i); // 从后往前查找
    return i;  //若查找成功，则返回元素下标，若查找失败，则返回0 
}

S.elem[0]称为哨兵，引入它使得查找函数的循环不必判断数组是否会越界，提高程序效率。

从尾部往前扫描，一旦触碰到哨兵，则查找失败。

不带哨兵的顺序查找代码如下
//普通顺序查找方法
int Search_Seq(SSTable S, ElemType key) {
	//在顺序表ST中顺序查找其关键字等于key的数据元素。若找到，则函数值为该元素在表中的位置否则为0
	for (int i = 1; i <= S.TableLen; i++) {
		if (S.elem[i] == key) {
			return i;
		}
	}
	return 0;
}
本代码以顺序存储结构为例，只是查询的情况下，顺序存储时间效率高于链式存储

以哨兵在顺序表，进行顺序查找算法为例

查找失败时，
假设没有元素相等，则需要比较到哨兵位置，即 $ASL_{lose}=n+1$

查找成功时，

假设第i个元素相等，需要进行n-i+1次比较（i为位序）

比如在0，1，2，3中，0为哨兵，查找1，需要进行3次查找

n个元素，进行顺序查找

$ASL_{win}=\sum_{i=1}^{n}P_{i}(n-i+1)$

如果每个元素的查找概率相等， $P_{i}=1/n$

则 $ASL_{win}=\sum_{i=1}^{n}P_{i}(n-i+1)=\frac{1+2+3+...+n}{n}=\frac{n+1}{2}$

若能预先知道每个记录的查找概率，则应先对记录的查找概率进行排序，再计算ASL。

这个操作可能会导致原先有序的数据元素乱序，查找方法更改，如原本使用折半查找变不可以。

同时，会导致查找成功率上升，失败率也上升。

2、有序线性表的顺序查找（判定树）

待查找元素为key，当发现第i个元素关键字小于key，第i+1个元素关键字大于key，这是就可以返回查找失败的信息。

使用判定树来描述有序线性表的查找过程。图中圆形结点表示有序线性表中存在的元素，矩形结点称为失败结点。

若有n个结点，则有n+1个失败结点。

查找成功时，

在有序线性表的顺序查找中，查找成功的ASL和一般线性表的顺序查找一样。

查找失败时，

比如查找25，需要比较3次，第3次是25小于某个结点，查找失败。

比如查找70，需要比较6次，第6次是跟失败结点比较成功的情况，而前5次是跟失败结点比较成功的情况。

n个元素，在有序线性表中进行顺序查找，

$ASL_{lose}=\frac{1+2+3+...+n+n}{n}=\frac{n}{2}+\frac{n+1}{n}$

注意，此时直至n+1个结点才失败， $P_{i}=\frac{1}{n+1}$ 。

判定树的最后一层有两个叶子结点，右边的叶子结点也是需要比较n次，确定这个失败结点是导致查找失败的罪魁祸首。

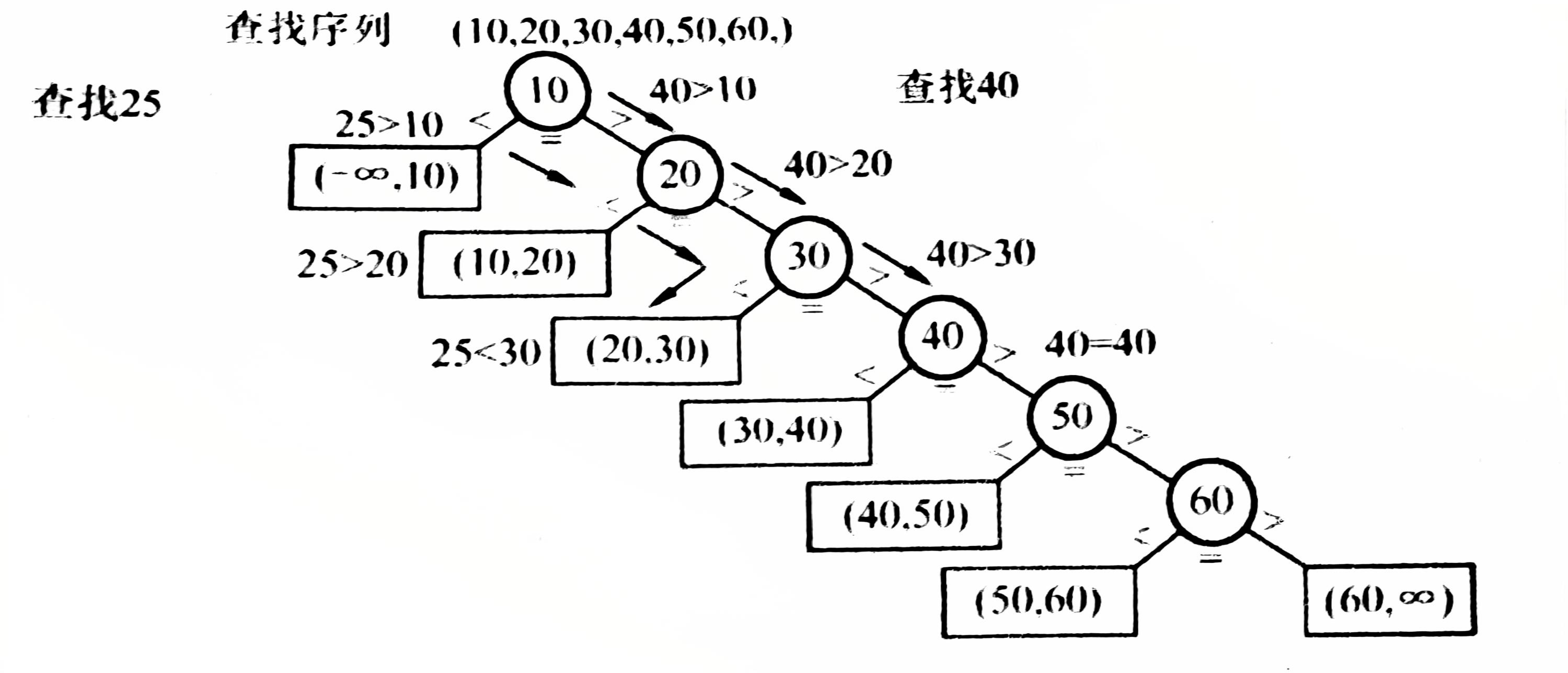
一个成功结点的查找长度=自身层数

一个失败结点的查找长度=其父节点所在层数

有序线性表的顺序查找和折半查找不一样，有序线性表的顺序查找仍可以使用链表，而折半查找只可以顺序存储结构。

二、折半查找

折半查找也称二分查找，要求线性表必须采用有序的顺序表

因为顺序表拥有随机存取的特性，而链表没有。

1、取数据集中间元素mid，与给定key比较，不等则下一步，相等则退出循环

2、如果key>mid，则key在右半部分数据集里，即左指标移至mid+1位；

如果key<mid，则key在左半部分数据集里，即右指标移至mid-1位；

3、再次重复步骤1，直至左指标小于右指标，此时如果需要插入数据，应该在右指标之后插入。

1、迭代实现折半查找

// 迭代实现折半查找
int binary_Search(SSTable S, ElemType key) {
    int low = 0, high = S.TableLen-1, mid;
    while (low <= high) {
        mid = (low + high) / 2; //向上取整，比如(2+3)/2=2 
        if (S.elem[mid] == key) {
            return mid;  // 搜索成功，返回目标元素的位置
        }
        else if (S.elem[mid] < key) {
            low = mid + 1;  // 在右半部分继续查找
        }
        else {
            high = mid - 1;  // 在左半部分继续查找
        }
    }
    return -1;  // 搜索失败，返回-1
}

2、折半查找判定树

每个结点值均大于其左子结点值，且均小于其右子结点值。

若有序序列有n个元素，则对应的判定树有n个圆形的非叶子结点和n+1个矩形叶子点。

显然，判定树是一颗平衡二叉树。

且同一个序列的折半查找的判定树唯一。

$mid = \left \lceil (low+high)/2 \right \rceil$ ，此时mid向上取整，右子树结点数-左子树节点数=0或1

反之，mid向下取整，左子树结点数-右子树结点数=0或1

如下图，mid向上取整，右子树结点数-左子树节点数=1

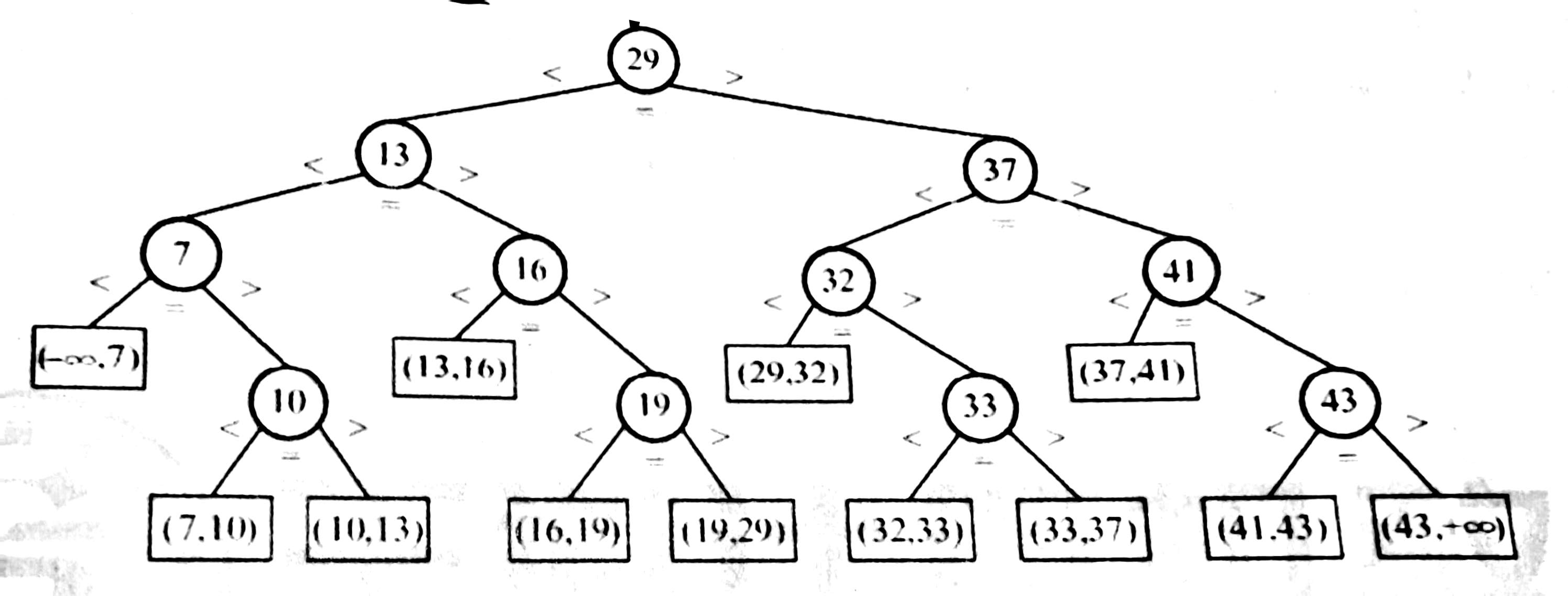
查找成功时的长度为从根节点到目的结点路径上的结点数。

查找失败时，查找长度为从根节点到对应失败结点的父节点的路径上的结点数。

用折半查找法查找到给定值的比较次数最多不会超过树的高度h，即最差时间复杂度O(h)

折半查找判定树的高 $h=\left \lceil log_{2}(n+1)\right \rceil$ ，折半查找时间复杂度为O( $log_{2}n$ )

在判定树中，

查找成功的平均查找长度 $ASL=\frac{1}{n}\sum_{i=1}^{n}l_{i} =\frac{1}{n}(1*1+2*2+3*4+...+h*2^{h-1})$

$=\frac{n+1}{n}log_{2}(n+1)-1$

$\approx log_{2}(n+1)-1$

图示中判定树，在等概率情况下，查找成功（圆形结点）ASL=(1*1+2*2+3*4+4*4)/11=3

查找失败（矩形结点）ASL=(3*4+4*8)/12=11/3

三、分块查找

分块查找又称索引顺序查找，它吸取顺序查找和折半查找的优点，既有动态结构，又适于快速查找。

将查找表分为若干子块。块内的元素可以无序，但块间的元素有序。

再建立一个索引表，索引表中每个元素含有各块的最大关键字和各块中的第一个元素的地址，索引表按关键字有序排列

查找过程

1、再索引表中确定待查记录所在的快，可以顺序查找也可以折半查找

2、在块内顺序查找

如果是在索引表进行折半查找

在low所指的分块中进行查找

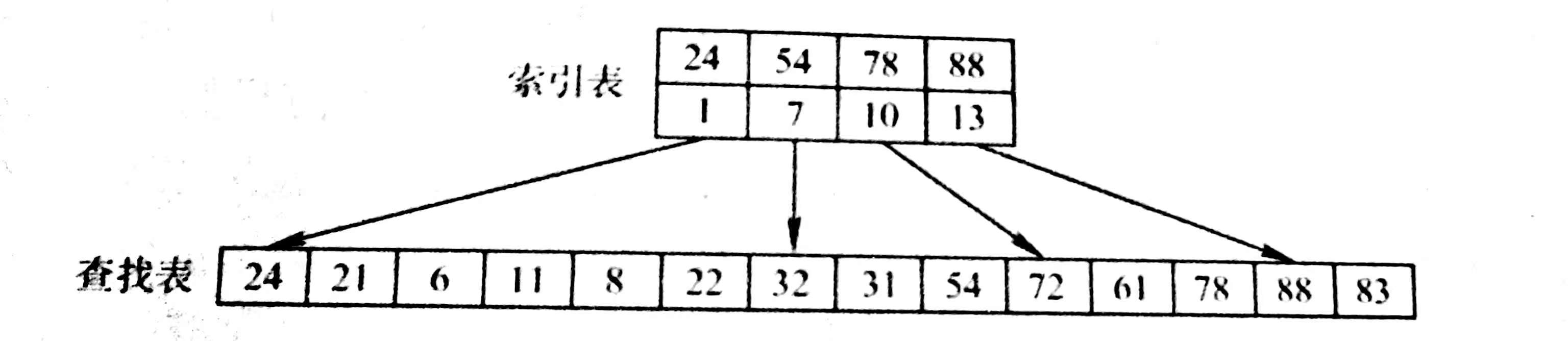
分块查找的平均查找长度为索引查找和块内查找的平均长度之和。

设索引查找和块内查找平均查找长度为L1和L2，则

ASL=L1+L2

将长度为n的查找表均匀的分为b块，每块有s个记录，在等概率的情况下，若在块内和索引表中均采用顺序查找，则

查找成功时，

$L1=\frac{1+2+3+...+b}{b}=\frac{b+1}{2}$ $L2=\frac{1+2+3+...+s}{s}=\frac{s+1}{2}$

$ASL=\frac{b+1}{2}+\frac{s+1}{2}=\frac{s^{2}+2s+n}{2s}$

当 $s=\sqrt{n}$ 时，最小 $ASL=\sqrt{n}+1$

如果折半查找，查找成功时， $ASL=\left \lceil log_{2}(b+1) \right \rceil+\frac{s+1}{2}$

四、各小节可运行完整代码

1、以顺序表作为存储结构，实现顺序查找（一般形式）和折半查找的算法

#include <stdio.h>
#include <stdlib.h>
 
typedef int ElemType;
// 定义结构体SSTable，表示顺序表
typedef struct {
    ElemType* elem;        // 动态数组基址 
    int TableLen;         // 表的长度
} SSTable;
 
// (哨兵方法） 函数Search_Seq1在顺序表S中顺序查找关键字等于key的数据元素
int Search_Seq1(SSTable S, ElemType key) {
	int i=0;
    S.elem[0] = key;  // 哨兵 
    for (i = S.TableLen; S.elem[i]!= key; --i); // 从后往前查找
    return i;  //若查找成功，则返回元素下标，若查找失败，则返回0 
}
 
//普通顺序查找方法
int Search_Seq(SSTable S, ElemType key) {
	//在顺序表ST中顺序查找其关键字等于key的数据元素。若找到，则函数值为该元素在表中的位置否则为0
	for (int i = 1; i <= S.TableLen; i++) {
		if (S.elem[i] == key) {
			return i;
		}
	}
	return 0;
}
 
// 迭代实现折半查找
int binary_Search(SSTable S, ElemType key) {
    int low = 0, high = S.TableLen-1, mid;
    while (low <= high) {
        mid = (low + high) / 2; //向上取整，比如(2+3)/2=2 
        if (S.elem[mid] == key) {
            return mid;  // 搜索成功，返回目标元素的位置
        }
        else if (S.elem[mid] < key) {
            low = mid + 1;  // 在右半部分继续查找
        }
        else {
            high = mid - 1;  // 在左半部分继续查找
        }
    }
    return -1;  // 搜索失败，返回-1
}
 
// 递归实现折半查找
int binary_Search2(SSTable S, int low, int high, ElemType key) {
    if (low > high) {
        return -1;  // 搜索失败，返回-1
    }
    int mid = (low + high) / 2;  // 计算中间位置
    if (S.elem[mid] == key) {
        return mid;  // 搜索成功，返回目标元素的位置
    }
    else if (S.elem[mid] < key) {
        return binary_Search2(S, mid + 1, high, key);  // 在右半部分继续查找
    }
    else {
        return binary_Search2(S, low, mid - 1, key);  // 在左半部分继续查找
    }
}

int main() {
    // 创建一个顺序表
    SSTable S;
    S.elem = (ElemType*)malloc(10 * sizeof(ElemType)); // 假设分配10个元素的空间
    S.TableLen = 0;   //初始化顺序表 
 
    // 向顺序表中添加元素
    S.elem[1]= 1;
    S.elem[2]= 2;
    S.elem[3]= 3;

    S.TableLen = 3;
 
    // 调用Search_Seq函数查找关键字为2的元素
    int position = Search_Seq1(S,2);
    if (position != 0) {
        printf("关键字位于 %d\n", position);
    }
    else {
        printf("没有找到关键字\n");
    }
 
    int position2 = Search_Seq(S,2);
    if (position2 != 0) {
        printf("关键字位于 %d\n", position2);
    }
    else {
        printf("没有找到关键字\n");
    }
    
    printf("迭代折半查找 位置为%d\n",binary_Search(S,2));
    printf("递归折半查找 位置为%d\n",binary_Search2(S,0,S.TableLen-1,2));

    // 释放顺序表空间
    free(S.elem);
 
    return 0;
}

2、以链表作为存储结构，实现顺序查找算法

#include <stdio.h>
#include <stdlib.h>
 
typedef struct ListNode {
    int data;
    struct ListNode* next;
} ListNode;
 
ListNode* InitializeList() {
    ListNode* head = (ListNode*)malloc(sizeof(ListNode));
    if (head != NULL) {
        head->data = 0;
        head->next = NULL;
    }
    return head;
}
 
ListNode* SequentialSearch(ListNode* head, int value) {
    ListNode* current = head;
    while (current != NULL) {
        if (current->data == value) {
            return current;
        }
        current = current->next;
    }
    return NULL;
}
 
int main() {
    ListNode* head = InitializeList();
    ListNode* node1 = (ListNode*)malloc(sizeof(ListNode));
    ListNode* node2 = (ListNode*)malloc(sizeof(ListNode));
 
    head->next = node1;
    node1->data = 1;
    node1->next = node2;
    node2->data = 2;
    node2->next = NULL;
 
    ListNode* result = SequentialSearch(head, 2);
    if (result != NULL) {
        printf("Found node with value %d\n", result->data);
    } else {
        printf("Node with value %d not found\n", 2);
    }
 
    // 释放链表内存等操作...
 
    return 0;
}

2、以链表作为存储结构，实现折半查找算法

#include <stdio.h>
#include <stdlib.h>
 
typedef struct ListNode {
    int data;
    struct ListNode* next;
} ListNode;
 
ListNode* InitializeList() {
    ListNode* head = (ListNode*)malloc(sizeof(ListNode));
    if (head != NULL) {
        head->data = 0;
        head->next = NULL;
    }
    return head;
}
 
ListNode* SequentialSearch(ListNode* head, int value) {
    ListNode* current = head;
    while (current != NULL) {
        if (current->data == value) {
            return current;
        }
        current = current->next;
    }
    return NULL;
}
 
int main() {
    ListNode* head = InitializeList();
    ListNode* node1 = (ListNode*)malloc(sizeof(ListNode));
    ListNode* node2 = (ListNode*)malloc(sizeof(ListNode));
 
    head->next = node1;
    node1->data = 1;
    node1->next = node2;
    node2->data = 2;
    node2->next = NULL;
 
    ListNode* result = SequentialSearch(head, 2);
    if (result != NULL) {
        printf("Found node with value %d\n", result->data);
    } else {
        printf("Node with value %d not found\n", 2);
    }
 
    // 释放链表内存等操作...
 
    return 0;
}

五、错题

下列选项中，不能构成折半查找中关键字比较序列的是 A

A、500、200、450、180 B、500、450、200、180

C、180、500、200、450 D、180、200、500、450

折半查找是一个二叉排序树，左<根<右

A 500
200
450
180
180不应该位于450的左子树，此时导致200的右子树存在元素小于200

B 500
450
200
180

C
180
500
200
450

D 180
200
500
450