差分数组的简介与应用

最新推荐文章于 2025-07-23 15:42:38 发布

Lee贤

最新推荐文章于 2025-07-23 15:42:38 发布

阅读量785

点赞数 3

CC 4.0 BY-SA版权

分类专栏：数据结构与算法文章标签：算法数据结构

本文链接：https://blog.youkuaiyun.com/m0_64707620/article/details/129469764

数据结构与算法专栏收录该内容

51 篇文章

订阅专栏

1.问题背景引入

Sample Input 1 :

Sample Output 1:

7
6

问题背景其实就是在数组规模非常大的前提下，想要对数组就行批量的，连续区间的操作（差分数组的原理前提条件），如何在时间复杂度最优的情况下设计更好的算法来实现。

2.差分数组原理简介和应用

所谓差分数组，就是利用数组相邻元素作差来保存在另一个新开辟的数组中，当我们对数组的任意一块连续的区间进行操作时，我们就可以只操作差分数组左边界和右边界加1的两处下标上的值，因为我们的差分数组就是在原数组相邻元素之差上实现的，在区间内的相同操作，只会影响差分数组边界的值，不会影响其内部的值，这样对于规模较大的数据，在进行连续区间操作时，我们可以通过操作差分数组的边界值，一次操作只改变两个值就可以实现目标，大大提高效率。

现在我们回到我们的背景题目中去，套用模板，我们可以轻松的写出差分数组，这里我们需要注意，差分数组在计算某个下标的最终值时，我们需要采用递推的方式来计算，从第一个开始，一次推导出后面的值，而第一个值就是差分数组的第一个值，这里我们通常将差分数组和原数组的下标0的位置设为0，并且从下标1开始统计输入，可以方便差分数组的计算。

#include<stdio.h>//uncle-lu
//我们对修改的部分进行差分，每次操作只会用两次操作，降低了一维的时间复杂度。
int line[10010];
int change[10010];//修改的部分的差分
int n, q, p;

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
		scanf("%d", &line[i]);

	scanf("%d", &q);
	for (int i = 1; i <= q; ++i)
	{
		int a, b, val;
		scanf("%d %d %d", &a, &b, &val);
		change[a] += val;
		change[b + 1] -= val;//objective 1利用差分修改change数组
        //注意这里影响的是下标为b+1的值，并不是b下标的值
	}
	/*for (int i = 1; i <= n; i++)
		printf("%d ", change[i]);
	printf("\n");*/
	for (int i = 1; i <= n; i++)
	{
		change[i] +=( line[i] - line[i - 1]);
		
	}//objective 2将差分数组抹平 
	for (int i = 1; i <= n; i++)
		line[i] = line[i - 1] + change[i];//递推求出原数组
	/*for (int i = 1; i <= n; i++)
	{
		printf("%d ", change[i]);
	}
	printf("\n");*/
	/*for (int i = 1; i <= n; i++)
	{
		printf("%d ", line[i]);
	}*/

	scanf("%d", &p);
	for (int i = 1; i <= p; ++i)
	{
		int temp;
		scanf("%d", &temp);
		printf("%d\n", line[temp]);//objective 3答案是什么？
	}

	return 0;
}

3.拓展应用

我们都知道，算法真正困难的就是将实际问题转化为数学模型来进行解题，这应该也是大部分同学做算法题没有突破的原因，我们刷题的目的不在做多少题，而在于练习我们抽象出问题的能力，下面我们再来看一道题：

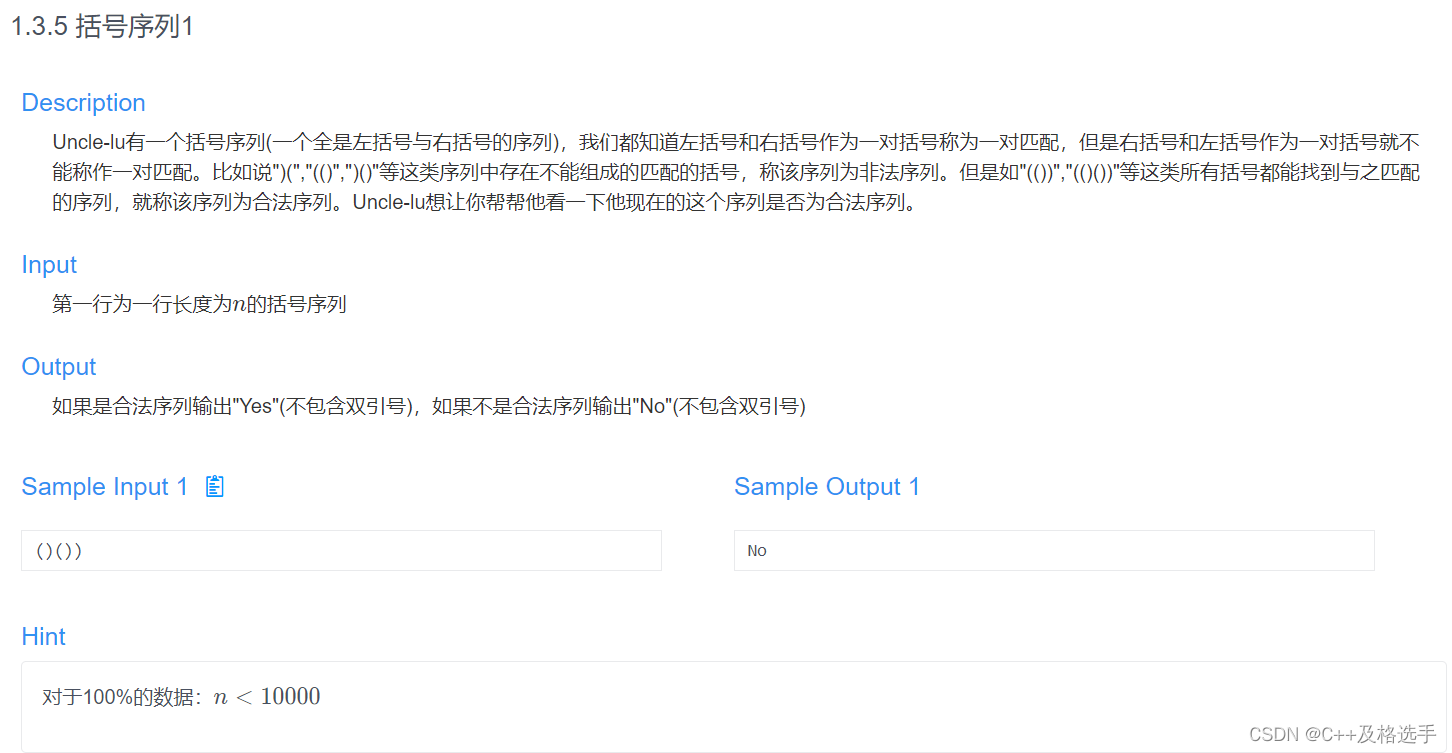
上来一看题我们第一个是不是就想到用栈直接模拟，我们回头想一想，我们这次学了差分数组，而作者又将这道题放在这，很明显是要我用差分数组试一试啊，那么我们来慢慢找思路.....

首先，我们注意到如果要括号匹配，那么左括号数量一定等于右括号数量，接着，我们再想，单单这样的话可以吗，如果是这样 “（））（” 的例子，是不是会被误判呢？如果用差分数组的形式，那么相邻的差值有什么联系呢？如果我们把 '('看做1，把')'看做-1，在遍历原数组的过程中对其进行差分数组操作，那么如果括号匹配的话，差分数组前半部分应该是大于0的数表示的是'('的累加结果，遇到')'时，我们将其和前面差分数组的累加和进行相加，可以起到抵消前面的一个'('的效果，再执行的过程中，如果遇到“（））（”情况，在差分数组中一定会出现小于0的情况，我们将这种情况视为匹配失败即可避免，现在思路就非常清晰了，我们直接来看代码。

#include<stdio.h>//uncle-lu
#include<string.h>
//利用差分来找是否有未配对）在（前面的
char line[10010];
int flag[10010];

int main()
{
	scanf("%s",line+1);

	int len = strlen(line+1);

	for(int i=1; i<=len; ++i)
	{
		if(line[i]=='(')flag[i] = 1;
		else flag[i] = -1;
		flag[i]+=flag[i-1];//objective 2抹平差分数组
	}

	bool f = true;
	for(int i=1; i<=len; ++i)
	{
		if(flag[i]<0)f = false;//objective 1什么情况是发现了故障？
	}
	if(f)
		printf("Yes");
	else
		printf("No");

	return 0;
}

可见，差分数组的应用场景还是很多的，只要是涉及相邻元素的关系运算，和相关地区间操作都可以用，不过瘾我们再来一道题

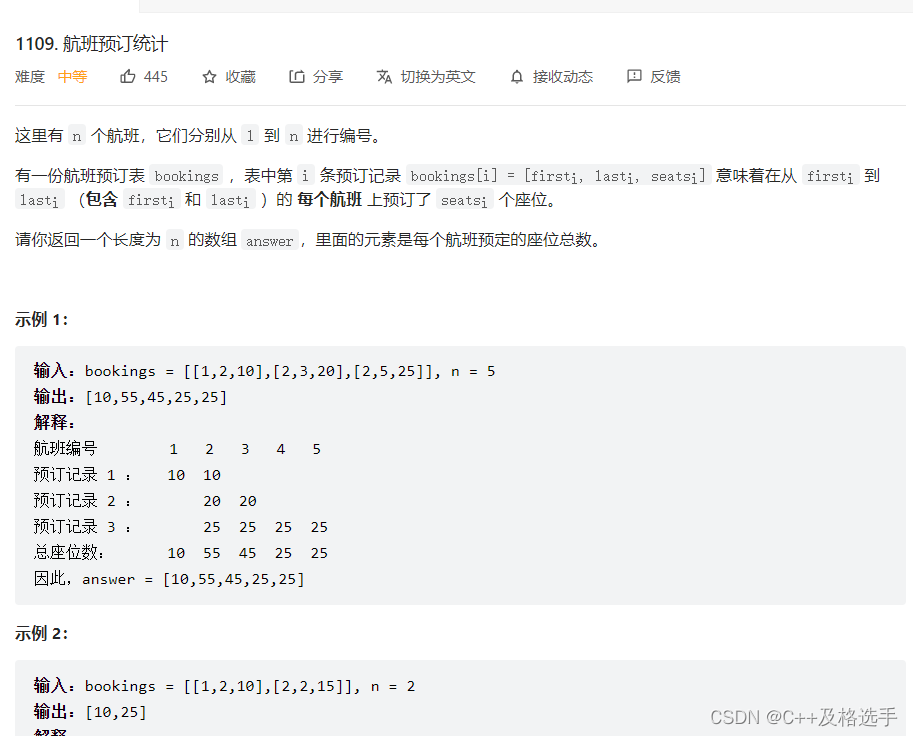
leetcode上的中档题了，我们来用差分数组，只需要注意数组范围尽量大一些避免越界即可。

class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> ans(n+10,0);
        vector<int> change(n+10,0);
        for(int i=0;i<bookings.size();i++)
        {
            change[bookings[i][0]]+=bookings[i][2];
            change[bookings[i][1]+1]-=bookings[i][2]; 
        }
        //差分数组统计
        for(int i=1;i<=n;i++)
        {
            ans[i]=ans[i-1]+change[i];
        }
        
        ans.assign(ans.begin()+1,ans.begin()+n+1);
        //这个assign函数有必要说一下，这是一个vector的区间截取函数，用来截取两个地址之间的区间部分
        return ans;
    }
};

好了，差分数组的讲解就到这里了，大家下期见......