【C语言】算法学习·线段树

当我们需要查询数组区间和，当数组为静态时，显然数组前缀和更方便，但是当数组需要动态更新的话，数组前缀和就显得乏力，所以我们需要引用线段树

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶子结点。使用线段树可以快速以O(logN)的时间复杂度实现单点、区间的修改和查询，综合性能较好。对于线段树中的每一个非叶子结点[i, j]，它的左儿子表示的区间为[i, (i + j)/2]，右儿子表示的区间为[(i + j)/2 + 1, j]，因此线段树是平衡二叉树。

以数组arr = [1, 2, 3, 5, 7]为例，我们可以画出以下的线段树，每个结点的值表示对应区间的元素和，叶子结点表示单个元素的值，非叶子结点表示的区间和等于两个儿子结点的和，因此我们可以通过自底向上的递归来构建一颗线段树。由于线段树与完全二叉树十分相似，于是我们可以用一个数组来模拟二叉树，根节点为0的话，那么每个结点的左儿子结点就等于当前结点的下标*2+1，右儿子的下标为当前结点的下标 * 2 + 2。

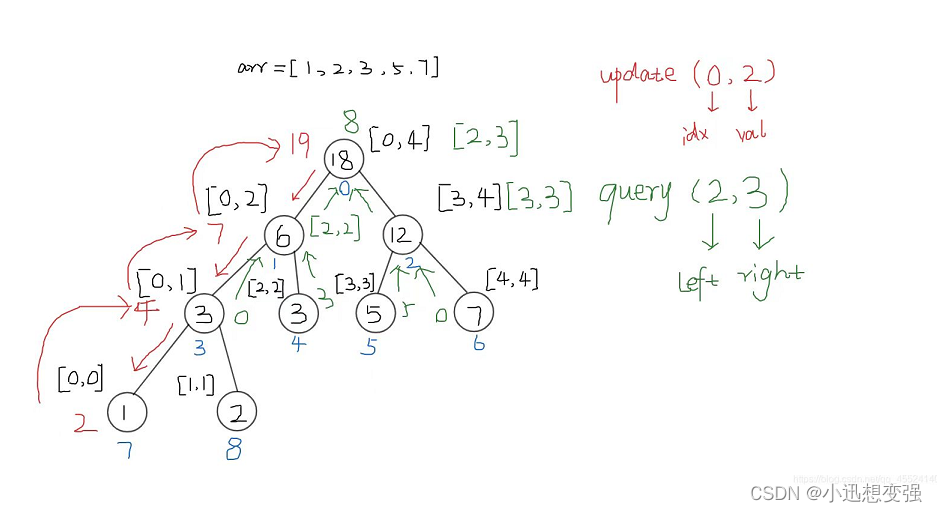
递归实现创建线段树 

        树实现

NumArray * TreeCreate(int left, int right, int * nums, int mid)
{
    if(mid == left && mid == right)//到达数组单个节点
    {
        NumArray * obj = malloc(sizeof(NumArray));
        obj->sum_val = nums[mid];
        obj->index_left = left;
        obj->index_right = mid;
        obj->tree_left = NULL;
        obj->tree_right = NULL;
        return obj;
    }
    else
    {
        NumArray * root = malloc(sizeof(NumArray));//创建树节点，将数组分割保存，左子树保存数组左边，右子树保存数组右边
        root->index_left = left;
        root->index_right = right;
        root->tree_left = TreeCreate(left, mid, nums, (left + mid) / 2);
        root->tree_right = TreeCreate(mid + 1, right, nums, (right + mid + 1) / 2);
        root->sum_val = root->tree_left->sum_val + root->tree_right->sum_val;
        return root;
    }
}

        树状数组

void BuildTree(NumArray* obj, int start, int end, int pos){
    if(start == end){
        obj->Tree[pos] = obj->arr[start];
        }
    else{
        int mid = (start + end) / 2;
        int left_node = pos * 2 + 1;
        int right_node = pos * 2 + 2;
        BuildTree(obj, start, mid, left_node);
        BuildTree(obj, mid + 1, end, right_node);
        obj->Tree[pos] = obj->Tree[left_node] + obj->Tree[right_node];
        }
}

 

如果要实现单点更新，我们不难想到，只要找到对应的叶子结点，修改后，自底向上返回即可，这与二叉搜索树类似，不过比较的是元素所属的区间，可以想到区间修改也是类似的操作，找到对应的元素修改即可

         树实现

/*
*void numArrayUpdate(NumArray* obj, int index, int val)
void numArrayUpdate：修改数组元素
NumArray* obj：数组对应线段树头结点
int index：待修改元素下标
int val:带修改元素值
无返回值
*/
void numArrayUpdate(NumArray* obj, int index, int val) {
    if(obj->index_le