例题:
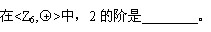
解析:

即对于模n加法来说,其相加的俩个数中任意一个数通过幂运算(幂运算的执行运算根据代数系统中的算符而定)能够整除6
而且单位元是0的原因:
因为最后是求的余数
例题:

 这篇博客探讨了模n加法中涉及的幂运算概念,指出任意两个相加的数通过幂运算都能被6整除。强调了在求余数运算中单位元为0的重要性,并通过实例进一步阐述了这一数学原理。
这篇博客探讨了模n加法中涉及的幂运算概念,指出任意两个相加的数通过幂运算都能被6整除。强调了在求余数运算中单位元为0的重要性,并通过实例进一步阐述了这一数学原理。
例题:
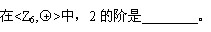
解析:

即对于模n加法来说,其相加的俩个数中任意一个数通过幂运算(幂运算的执行运算根据代数系统中的算符而定)能够整除6
而且单位元是0的原因:
因为最后是求的余数
例题:

 1万+
1万+
 3959
3959
 1740
1740

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


