Syntax-Aware Complex-Valued Neural Machine Translation

摘要

语法已被证明在神经机器翻译 (NMT) 中非常有效。以前的模型从句法解析工具中获得了句法信息，并将其集成到 NMT 模型中以提高翻译性能。在这项工作中，我们提出了一种将语法信息合并到复值编码器-解码器架构中的方法。所提出的模型使用注意力机制从源端到目标端联合学习词级和句法级注意力分数。重要的是，它不依赖于特定的网络架构，可以直接集成到任何现有的序列到序列 (Seq2Seq) 框架中。实验结果表明，所提出的方法在两个数据集上可以显着提高 BLEU 分数。特别是，所提出的方法在涉及具有显着句法差异的语言对的翻译任务中实现了 BLEU 分数的更大改进。
关键词：Neural machine translation, Attention mechanism, Complex-valued neural network.

1 介绍

近年来，神经机器翻译 (NMT) 受益于序列到序列 (Seq2Seq) 框架和注意力机制。NMT 在各种语言对中显示出比统计机器翻译 (SMT) 模型的有效改进。基于注意力的编码器-解码器架构将源语言句子编码为一系列隐藏的实值向量，然后根据注意力机制计算它们的加权和，以生成解码器中的目标语言句子预测。
语法信息已广泛用于 SMT中并被证明是有效的，研究人员还尝试将语法信息整合到 NMT 中。一些研究已经证明了语法信息的重要性，这也在这项工作中简要讨论。例如，在句子“He saw her duck”中，根据图 1 所示的句法分析结果，当“duck”用作“her”的属性时，这意味着“a duck”。在这种情况下，“duck”和“her”之间的依赖关系是 poss（所有格）。然而，当“duck”被用作“her”的谓语时，这意味着“to dodge”、“to avoid”或“to duck down”。在这种情况下，“duck”和“her”之间的依赖关系是nsubj(名词主语)。这表明句法信息在很大程度上影响着单词的意思。

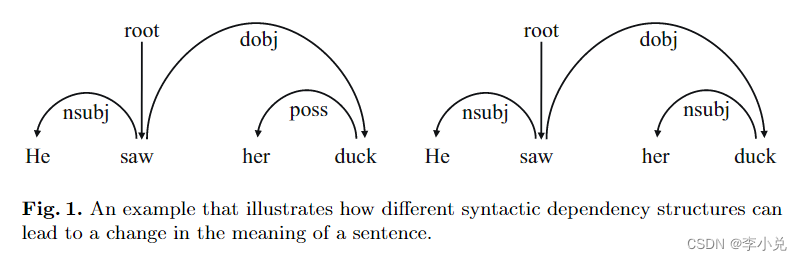
相当多的研究人员将句法信息集成到 NMT 中以提高翻译性能。这些研究中的大多数都在源端集成了语法。然而，在现实中，句法依赖关系因不同语言而异。因此，先前的研究缺乏对不同语言的句法依赖的匹配。如图 2 所示，考虑中文句子“他在公园里散步”。它的英文翻译“He went for a walk in the park.”这两个句子传达了相同的含义，即描述某人在公园里行走。然而，从句法分析的角度来看，它们并不完全相同。

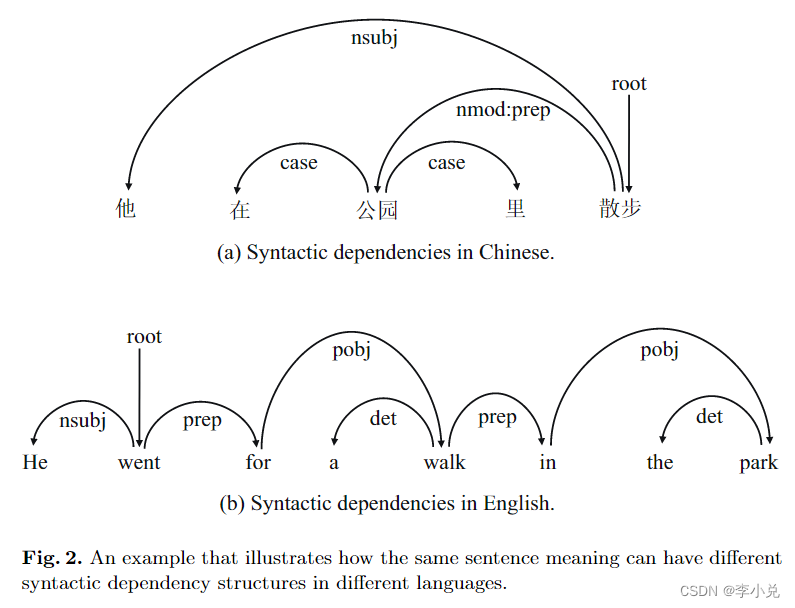
最近关于循环神经网络的工作和基本理论的分析表明，复数可能具有更丰富的表征能力。许多研究人员一直热衷于扩展复值神经网络 (CVNN)，其中复数被视为固定参数或无意义的附加参数。然而，这些做法显着限制了 CVNN 的泛化能力和可解释性。
在这项工作中，来自不同语言的句法信息被嵌入到 CVNN 中。复值注意力机制用于对复值隐藏向量进行评分，旨在联合学习单词和句法的注意力分数。这种方法不依赖于特定的模型架构，可以应用于任何现有的 Seq2Seq 架构。我们的核心思想是具有不同句法依赖的相同词可能具有不同的含义。这种复杂的词嵌入方法可以在一定程度上缓解多义引起的翻译错误。我们对汉英和英德翻译任务进行了实验。实验结果表明，我们的方法非常有效，尤其是对于长句。

2 背景

2.1 神经机器翻译(Neural Machine Translation)

典型的神经机器翻译系统是一种基于注意力的 Encoder-Decoder 架构，典型的神经机器翻译系统是一种基于注意力的编码器-解码器架构，它通过将源句子$x_1,...,x_n$计算到目标句子$y_1,...,y_m$来对条件概率$p(y|x)$进行建模。编码器用于获得源语句的表示，解码器一次生成一个目标词。条件概率可以分解为：
$$logp(y|x)=\sum _{j=1}^{m}logp(y_j|y<j,s)\text{\hspace{1em}(1)}$$
循环神经网络 (RNN) 通常被选为编码器和解码器，包括长短期记忆 (LSTM) 或门控循环单元 (GRU)。以RNN为例，时间$t$的隐藏状态$h_t$为:
$$h_t=tanh(W_{ih}{x}_t+b_{ih}+W_{hh}{h}_{t-1}+b_{hh})\text{\hspace{1em}(2)}$$
其中$x_t$是时间$t$的输入，$h_{t-1}$是时间$t-1$的隐藏状态。用作解码器的输入的上下文向量$c_i$被计算为这些$h_t$的加权和：
$$c_i=\sum _{j=1}^n{\alpha }_{ij}{h}_j\text{\hspace{1em}(3)}$$
每个隐藏状态$h_j$的权重${\alpha }_{ij}$计算为:
$${\alpha }_{ij}=\frac{exp(e_{ij})}{{\sum }_{k=1}^{n}exp(e_{ik})}\text{\hspace{1em}(4)}$$
其中$e_{ij}=a(s_{i-1},h_j)$是一个对齐模型，$s_{i-1}$表示解码器在时间$i-1$的隐藏状态。

2.2 复值神经网络(Complex-valued Neural Network)

复数可以表示为$z=a+ib$，其中$a$是实部，$b$是虚部，$i$是虚数。在CVNN中，复值向量可以表示为：
$$h=x+iy\text{\hspace{1em}(5)}$$
其中$x$和$y$是实值向量。复值矩阵可以表示为：
$$W=A+iB\text{\hspace{1em}(6)}$$
其中$A$和$B$是实值矩阵。复值矩阵与复值向量的乘积的计算规则如下：
$$Wh=(Ax-By)+i(Bx+Ay)\text{\hspace{1em}(7)}$$
可以用矩阵表示法表示如下：
$$\left[\begin{array}{c}\mathfrak{R}(Wh)\\ \mathfrak{I}(Wh)\end{array}\right]=\left[\begin{array}{c}A-B\\ BA\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\text{\hspace{1em}(8)}$$
复值激活函数（例如 ReLU）可以表示为：
$$\mathbb{C}ReLU(z)=ReLU(\mathfrak{R}(z))+iReLU(\mathfrak{I}(z))\text{\hspace{1em}(9)}$$

3 提出的方法

在本节中，我们将详细介绍我们提出的方法（基本结构如图 3 所示）。我们将其称为语法感知复值神经机器翻译(SynCoNMT)。为简单起见，我们首先同意使用以下符号来表示张量的一般复值形式：
$$\mathbb{C}(z)=\mathfrak{R}(z)+i\mathfrak{I}(z)\text{\hspace{1em}(10)}$$
其中$z$可以是任意形状的张量。$\mathfrak{R}(z)$和$\mathfrak{I}(z)$分别表示复张量$z$的实部和虚部。

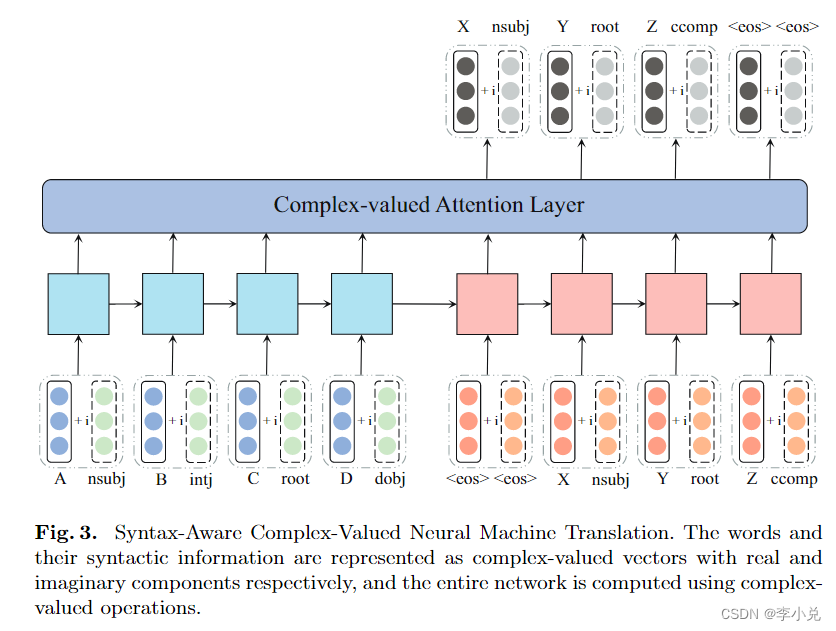
3.1 语法嵌入(Syntax Embedding)

在这项工作中，我们使用 CVNN 将单词和句法信息分别表示为复值向量的实部和虚部。我们将此嵌入称为语法嵌入 (SE)。词向量和依赖向量分别从词和依赖查找表中获得。单词$w$的SE，表示为$\mathbb{C}(s_{ij})$，表示单词$w_i$在特定句法依赖关系$d_j$中的含义，定义如下：
$$\mathbb{C}(s_{ij})=w_i+i{d}_j=\mathfrak{R}(s_{ij})+i\mathfrak{I}(s_{ij})\text{\hspace{1em}(11)}$$
此外，单词$w_i$在依赖关系$d_j$和$d_k$下的含义可以用两个嵌入$\mathbb{C}(s_{ij})$和$\mathbb{C}(s_{ik})$表示，它们具有相同的实部但虚部不同。

3.2 复值神经机器翻译(Complex-valued Neural Machine Translation)

我们提出的 SynCoNMT 接受复值句法嵌入（如第 3.1 节所述），并预测目标词的条件概率分布。编码器和解码器使用复值 RNN 架构进行计算。具体来说，时间$t$的隐藏状态$\mathbb{C}(h_t)$是：
$$\mathbb{C}(h_t)=\mathbb{C}tanh(\mathbb{C}(W_{ih}{x}_t))+\mathbb{C}(W_{hh}{h}_{t-1})+\mathbb{C}(b_{hh})\text{\hspace{1em}(12)}$$
复值上下文向量$\mathbb{C}(c_i)$使用复值注意力分数计算为隐藏状态$\mathbb{C}(h_t)$的加权和，如下所示：
$$\mathbb{C}(c_i)=\sum _{j=1}^n\mathbb{C}({\alpha }_{ij})\mathbb{C}(h_j)\text{\hspace{1em}(13)}$$
每个复值隐藏状态$\mathbb{C}(h_j)$的权重$\mathbb{C}({\alpha }_{ij})$计算如下：
$$\mathbb{C}({\alpha }_{ij})=\mathbb{C}Softmax(\mathbb{C}(e_{ij}))\text{\hspace{1em}(14)}$$
其中$\mathbb{C}(e_{ij})=\mathbb{C}align(\mathbb{C}(s_{i-1}),\mathbb{C}(h_j))$是一个复值对齐模型，遵循第 2.2 节中描述的复值计算规则。复值注意力分数对词向量和句法向量进行加权，允许解码器同时关注语义和句法信息。

3.3 基于语法的损失函数(Syntax-based Loss Function)

我们提出的模型同时预测单词和语法，并使用预测的单词作为最终的翻译结果。我们使用两个复值全连接层分别将解码器的隐藏状态$s_i$映射到单词和依赖空间:
$$\widehat{y_w}=|\mathbb{C}Linea{r}_w(\mathbb{C}(s_i))|\text{\hspace{1em}(15)}$$
$$\widehat{y_d}=|\mathbb{C}Linea{r}_d(\mathbb{C}(s_i))|\text{\hspace{1em}(16)}$$
其中$|\cdot |$表示复值向量中每个元素模量的计算。我们使用交叉熵损失函数联合计算预测单词和语法依赖关系的损失。形式化如下：
$$\mathcal{L}=\alpha {\mathcal{L}}_w(y_w,\widehat{y_w})+(1-\alpha ){\mathcal{L}}_d(y_d,\widehat{y_d})\text{\hspace{1em}(17)}$$
其中$\alpha$是一个超参数，$\widehat{y_{\ast }}$是单词或依赖的预测分布，损失项${\mathcal{L}}_w(y_w,\widehat{y_w})$和${\mathcal{L}}_d(y_d,\widehat{y_d})$分别由(18)和(19)给出:
$${\mathcal{L}}_w(y_w,\widehat{y_w})=-\sum _{i=1}^{|V|}{y}_w^{(i)}log({\hat{y}}_w^{(i)})\text{\hspace{1em}(18)}$$
$${\mathcal{L}}_d(y_d,\widehat{y_d})=-\sum _{i=1}^{|V|}{y}_d^{(i)}log({\hat{y}}_d^{(i)})\text{\hspace{1em}(19)}$$
其中$|V|$和$|D|$分别是单词查找表和依赖查找表的大小。

4 实验

4.1 设置

我们在两个数据集上进行了实验。首先，我们在来自 LDC 语料库 1 的 1.25 亿个句子对数据集上进行训练，用于汉英句子对。然后，我们使用 NIST MT02 作为开发集，NIST MT03、04、05 和 06 作为测试集。我们还使用 WMT’14 中针对英德句子对使用了 4370 万个句子对进行了实验，newstest2012 作为开发集，newstest2013、newstest2014 和 newstest2015 作为测试集。所有语言都使用 SpaCy进行标记化和句法依赖解析。最后，我们总是使用单个句子作为参考进行评估，使用不区分大小写的 4-gram BLEU 分数。
对于模型的超参数，所有隐藏状态都设置为 512 维。源语言和目标语言的词嵌入和依赖嵌入维度都设置为 512。训练继续进行，直到开发集的 BLEU 分数没有提高 5 个连续 epoch。

4.2 基线系统

4.3 评估 SynCoNMT

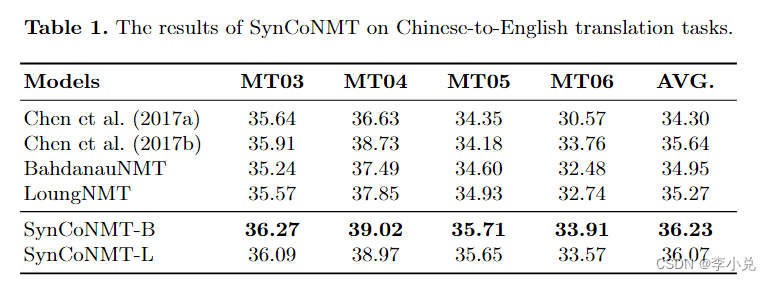
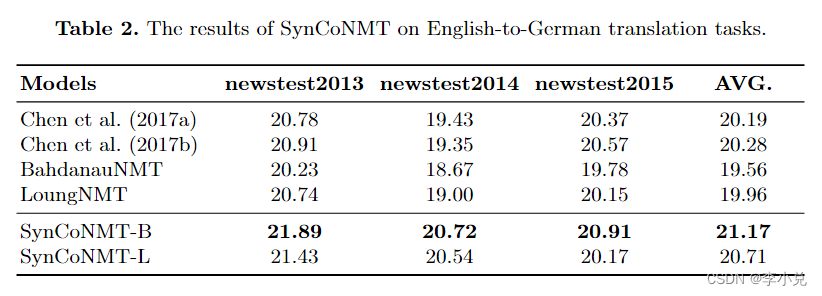
表 1 和表 2 分别显示了第 3 节中介绍的 SynCoNMT 在汉英和英德翻译任务上的翻译结果。我们分别基于基线模型 BahdanauNMT和 LoungNMT实现了 SynCoNMT-B 和 SynCoNMT-L，以证明所提出方法的有效性。虽然 Chen 等人提出的基于语法的方法。 (2017a) 并不总是优于基于注意力的方法，但它表明句法信息对 NMT 很有价值。
在汉英翻译任务中，SynCoNMT 将 BahdanauNMT 和 LoungNMT 的性能分别提高了 1.28 和 0.80 BLEU 点。这表明 SynCoNMT 可以有效地提高 NMT 的翻译性能。同样，在英德翻译任务中，SynCoNMT 平均提高了 BahdanauNMT 和 LoungNMT 的性能，平均 BLEU 点分别为 1.61 和 0.75。这表明 SynCoNMT 是一种稳健的方法。
具体来说，与 Chen 等人提出的基于语法的方法相比。 (2017a)，SynCoNMT 获得了更高的 BLEU 分数，这表明将句法信息纳入 CVNN 很有价值。
值得注意的是，尽管 LoungNMT 比基线中的 BahdanauNMT 更有效，但 SynCoNMT 在 BahdanauNMT 上的表现优于 LoungNMT。这表明句法嵌入在考虑整体句子信息时更有效，因为句法树本质上是一个具有整体性质的树结构。

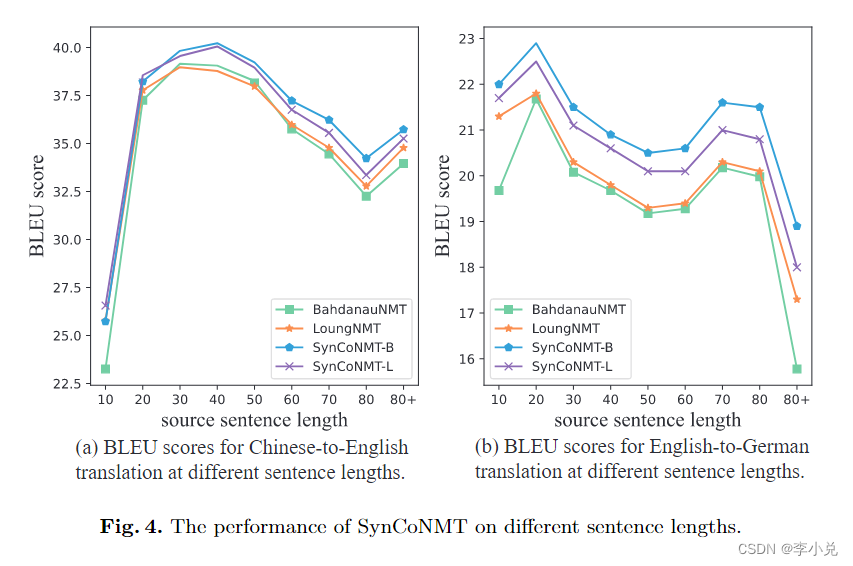
4.4 翻译长句的影响

我们在两个任务的测试集中分组了相似长度的句子，以评估BLEU的性能。例如，句子长度“30”表示源长度在20到30之间的句子。然后，我们计算各组BLEU评分，结果如图4(a)和图4(b)所示。在两个翻译任务中，SynCoNMT在不同长度的句子上产生的BLEU分数始终高于基线BahdanauNMT和LoungNMT。特别是在处理较长句子方面，SynCoNMT-B的BLEU分数明显高于其他方法。这是因为我们的方法更关注源句和目标句之间的句法匹配，而不仅仅是考虑一方(源句或目标句)的句法结构。此外，复杂嵌入的使用允许在预测输出上联合单词和语法约束，从而提高了NMT的性能。

4.5 复值注意力

图 5 说明了一个示例，其中复值的注意力分数与传统的注意力分数不同。在句子级别，复值注意力分数的实部倾向于更多地关注与其具有句法依赖的单词。在依赖级别，复值注意力分数的虚部集中在句法依赖关系上。通过联合加权复杂的嵌入，模型通过解码器预测目标句子及其对应的语法。这进一步证明了 SynCoNMT 的鲁棒性。

5 相关工作

在本节中，我们将介绍基于语法的 NMT 和 CVNN 的相关工作。
句法信息已被证明在 SMT 中是有效的 [10,23]。因此，关于如何将句法信息纳入 NMT 已经做了很多工作。使用 LSTM 或 GRU 对句法树进行建模是一种常见的做法 [14,9]。Hashimoto等人[6]提出将头部信息与序列词相结合作为输入，并使用潜在依赖图对句法信息进行建模。Chen等人[3]使用卷积神经网络来表示依赖树。Wu等人[24]通过多个BiRNN集成句法信息。基于语法的 NMT 研究非常活跃，但以前的方法侧重于对源语言中的句法信息进行建模，而忽略了目标语言中的句法信息。
近年来，CVNN 受到越来越多的关注，因为它们可以捕获单个网络中实部和虚部之间的相互关系。CVNN 的早期工作之一是 Hirose [7] 提出的复杂反向传播算法。该算法将反向传播算法扩展到复杂域，从而实现 CVNN 的训练。受Hirose工作的启发，Zhang等人[25]提出了复值卷积神经网络。Popa等人[16]提出了复杂的深度信念网络。Virtue等人[20]提出了一种使用CVNN进行指纹识别的方法，该方法表现出比实值同类方法更好的性能。Zhu等人[26]提出了一种基于四元数的卷积神经网络，并证明了其在图像分类和目标检测任务中的优越性。
然而，据我们所知，CVNN 尚未应用于 NMT 的 Seq2Seq 架构。因此，受 CVNN 中令人兴奋的工作的启发，我们研究了 CVNN 在 NMT 中的应用。

6 总结

在本文中，我们提出了 SynCoNMT，它采用句法信息的复值建模来提高 NMT 的性能。我们的方法不仅优于其实值对应物，而且优于其他基于语法的 NMT 方法。此外，与仅考虑源端语法的方法不同，SynCoNMT 考虑了源端和目标端的句法映射。实验和分析证明了我们方法的有效性。未来，我们将探索如何将我们的方法应用于其他任务。