排序不等式算法

安排他们的打水顺序才能使所有人的等待时间之和最小，则需要将打水时间最短的人先打水
证明：
不妨设

(1)i1i1 ≠ i2i2 ≠ i3i3 ≠ … ≠ inin
(2)i1i1~inin属于[1,n][1,n]
(3)t1t1 < t2t2 < t3t3 <… < tntn,

1、由i的任意性，打水的时间总和为ti1ti1 * (n - 1) + ti2ti2 * (n - 2) + … + tintin * (n - n)
=n * (ti1ti1 + ti2ti2 +… + tintin) - (ti1ti1 * 1 + ti2ti2 * 2 + … + tintin * n)

2、即相当于求 ti1ti1 * 1 + ti2ti2 * 2 + … + tintin * n 的最大值

3、假设ti1ti1 , ti2ti2 ,… , tintin是按自然顺序排好序时是最大值，即TmaxTmax = t1t1 * 1 + t2t2 * 2 + … + tntn
4、任意选择两项ta∗xta∗x,tb∗(x+c)tb∗(x+c),且tata < tbtb,c > 0,交换tata,tbtb位置得到tb∗xtb∗x,ta∗(x+c)ta∗(x+c) ,同时交换后不会对其他项造成影响
由于tata * x + tbtb * (x + c) = tata * x + tbtb * x + tbtb * c > tata * x + tbtb * x + tata * c = tbtb * x + tata * (x + c),即交换之后比原来的值更小.由于选取的任意性可得假设成立.

时间复杂度 O(nlogn)O(nlogn)
Java 代码
import java.util.*;

public class Main{

public static void main(String[] args) {
    Scanner scan = new Scanner(System.in);

    int n = scan.nextInt();
    int[] a = new int[n + 1];
    for(int i = 1;i <= n;i++)
    {
        a[i] = scan.nextInt();
    }
    Arrays.sort(a);
    long res = 0;
    for(int i = 1;i <= n;i++)
    {
        res += (a[i] * (n - i));
    }
    System.out.println(res);

}

}
题目描述
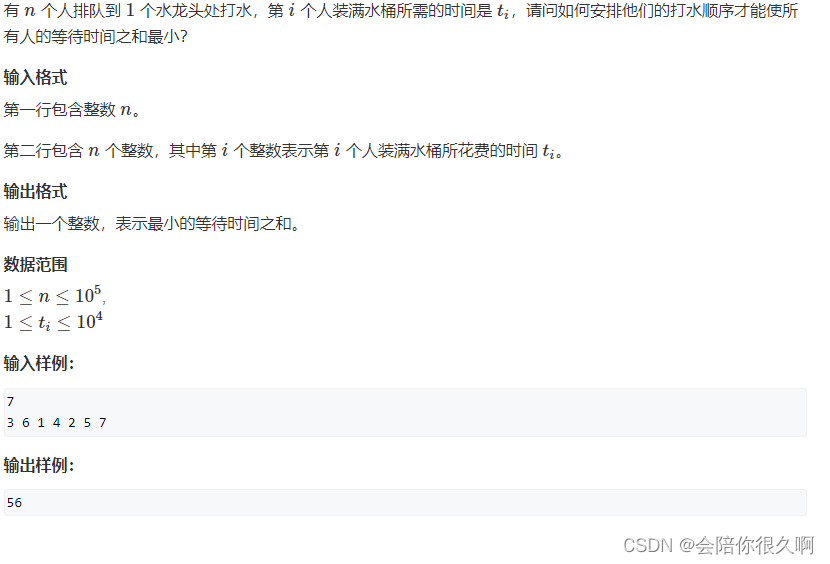
有 nn 个人排队到 11 个水龙头处打水，第 ii 个人装满水桶所需的时间是 titi ，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式
第一行包含整数 nn。

第二行包含 nn 个整数，其中第 ii 个整数表示第 ii 个人装满水桶所花费的时间 titi。

输出格式
输出一个整数，表示最小的等待时间之和。

数据范围
1≤n≤1051≤n≤105,
1≤ti≤1041≤ti≤104
输入样例：
7
3 6 1 4 2 5 7
输出样例：
56
算法(贪心)
首先，我们先想一种直觉上的做法。每次选一个当前序列中最小的一个数，然后让res加上本次的在总序列中耗费的时间，也就是 titi ×× (n−i−1)(n−i−1)，其中，titi是排好序中当前最小的，nn是数的个数，ii 是第 ii 个元素。然后我们再来证明它的正确性。假设有这样一个最优解序列cntcnt，排好序的序列中有一个数 cntxcntx，它的下一个数比它小，如果两数交换，(n−i−1)(n−i−1) ×× cnticnti - (n−i)(n−i) ×× cntxcntx的下一个数，差一定是严格>0>0的，这就和它是最优解矛盾了，所以最优解序列一定是单调上升的。

注意
res必须要是long long 类型的，因为titi最大是104104，nn最大是105105最大的数就是109109单调递减，105105凑起来一定会爆int。
写法一 朴素版
C++ 代码
#include
#include

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;

int t[N];

int main()
{
int n;
scanf(“%d”, &n);
for (int i = 0; i < n; i ++ ) scanf(“%d”, &t[i]);

sort(t, t + n);

LL res = 0;
for (int i = 0; i < n; i ++ )  res += t[i] * (n - i - 1);

printf("%lld\n", res);

return 0;

}
时间复杂度 O(nlogn)O(nlogn)
写法二 优先队列版
C++ 代码
#include
#include
#include

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;

int main()
{
int n;
scanf(“%d”, &n);

priority_queue<int, vector<int>, greater<int>> heap;

for (int i = 0; i < n; i ++ )
{
    int t;
    scanf("%d", &t);
    heap.push(t);
}

LL res = 0;
for (int i = 0; i < n; i ++ )
{
    int t = heap.top();heap.pop();
    res += t * (n - i - 1);
}
printf("%lld\n", res);

return 0;

}
时间复杂度 O(nlogn)O(nlogn)
写法三 手写堆版
C++ 代码
#include
#include
#include

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;

int h[N], Size = 0;
int n, m;

void down(int u)
{
int t = u;
if (u * 2 <= Size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= Size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
swap(h[u], h[t]);
down(t);
}
}

int main()
{
scanf(“%d”, &n);
for (int i = 1; i <= n; i ++ ) scanf(“%d”, &h[i]);

Size = n;

for (int i = n / 2; i; i -- )   down(i);

LL res = 0;

for (int i = 1; i <= n; i ++ )
{
    res += h[1] * (n - i);
    h[1] = h[Size --];
    down(1);
}

printf("%lld\n", res);

return 0;

}
时间复杂度 O(nlogn)O(nlogn)
手写堆：212 ms
朴素版：133 ms
优先队列版：480 ms