📌目录
一、表达式的基本概念
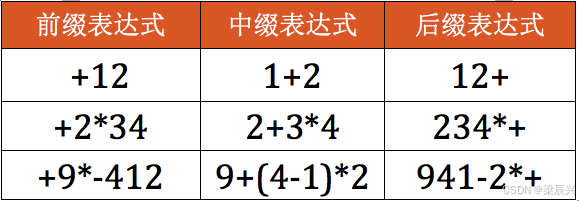
表达式是由操作数、运算符和界限符组成的有意义的序列。在计算机科学中,表达式的表示形式对算法设计和程序实现有着重要影响。常见的表达式表示形式有三种:前缀表达式、中缀表达式和后缀表达式。
1.1 操作数与运算符
- 操作数:可以是常量、变量或函数调用等
- 运算符:包括算术运算符(+、-、*、/等)、关系运算符(>、<、=等)和逻辑运算符(AND、OR、NOT等)
- 界限符:用于表示表达式的结构,如括号()
1.2 表达式的分类
| 表达式类型 | 定义 | 示例 |
|---|---|---|
| 前缀表达式 | 运算符位于操作数之前 | + 3 4 |
| 中缀表达式 | 运算符位于操作数之间 | 3 + 4 |
| 后缀表达式 | 运算符位于操作数之后 | 3 4 + |
二、中缀表达式(Infix Expression)
中缀表达式是我们日常使用最频繁的表达式形式,运算符位于两个操作数中间。
2.1 中缀表达式的特点
- 符合人类的思维习惯和书写习惯
- 存在运算符优先级和括号的问题
- 计算机处理中缀表达式需要解决运算符优先级判断和括号处理等问题
2.2 中缀表达式的求值过程
中缀表达式的求值是一个比较复杂的过程,需要考虑运算符的优先级和结合性。下面以表达式"3+4*2"为例说明求值过程:
- 首先确定运算符的优先级:*高于+
- 先计算4*2=8
- 再计算3+8=11
2.3 中缀表达式转后缀表达式
中缀表达式转后缀表达式是一个重要的操作,通常使用栈来实现。算法步骤如下:
- 初始化一个空栈和一个空列表
- 从左到右扫描中缀表达式
- 遇到操作数,直接加入列表
- 遇到运算符,与栈顶运算符比较优先级:
- 如果栈为空或栈顶为左括号,直接入栈
- 如果当前运算符优先级高于栈顶运算符,入栈
- 如果当前运算符优先级低于或等于栈顶运算符,弹出栈顶运算符加入列表,重复比较
- 遇到左括号,直接入栈
- 遇到右括号,弹出栈中运算符加入列表直到遇到左括号,左括号出栈但不加入列表
- 扫描结束后,将栈中剩余运算符依次弹出加入列表
- 列表中的元素即为后缀表达式
三、后缀表达式(Postfix Expression)
后缀表达式又称逆波兰表达式,运算符位于操作数之后。
3.1 后缀表达式的特点
- 没有运算符优先级的问题
- 不需要括号
- 计算机处理后缀表达式更加简单高效
- 求值过程可以通过栈轻松实现
3.2 后缀表达式的求值
后缀表达式的求值使用栈来实现,算法步骤如下:
- 初始化一个空栈
- 从左到右扫描后缀表达式
- 遇到操作数,压入栈中
- 遇到运算符,从栈中弹出相应数量的操作数,进行运算,将结果压入栈中
- 扫描结束后,栈顶元素即为表达式的值
3.3 后缀表达式求值示例
以后缀表达式"3 4 2 * +"为例:
- 扫描到3,压入栈,栈:[3]
- 扫描到4,压入栈,栈:[3,4]
- 扫描到2,压入栈,栈:[3,4,2]
- 扫描到*,弹出2和4,计算4*2=8,压入栈,栈:[3,8]
- 扫描到+,弹出8和3,计算3+8=11,压入栈,栈:[11]
- 扫描结束,结果为11
四、前缀表达式(Prefix Expression)
前缀表达式又称波兰表达式,运算符位于操作数之前。
4.1 前缀表达式的特点
- 与后缀表达式类似,但运算符在操作数之前
- 同样没有运算符优先级和括号的问题
- 求值过程也使用栈实现,但操作数的弹出顺序与后缀表达式不同
4.2 前缀表达式的求值
前缀表达式的求值同样使用栈,但扫描顺序是从右到左,算法步骤如下:
- 初始化一个空栈
- 从右到左扫描前缀表达式
- 遇到操作数,压入栈中
- 遇到运算符,从栈中弹出相应数量的操作数,进行运算,将结果压入栈中
- 扫描结束后,栈顶元素即为表达式的值
4.3 前缀表达式求值示例
以前缀表达式"+ 3 * 4 2"为例:
- 从右到左扫描,首先遇到2,压入栈,栈:[2]
- 遇到4,压入栈,栈:[2,4]
- 遇到*,弹出4和2,计算4*2=8,压入栈,栈:[8]
- 遇到3,压入栈,栈:[8,3]
- 遇到+,弹出3和8,计算3+8=11,压入栈,栈:[11]
- 扫描结束,结果为11
五、三种表达式的转换方法
5.1 中缀转前缀:镜像翻转法
核心思路:把中缀表达式倒过来处理,转换逻辑类似"中缀转后缀",最后再翻回来。
案例:中缀表达式 (3+4)*2 转前缀
分步拆解(像照镜子一样反转操作):
- 反转中缀表达式:
2*(4+3)(注意括号也要反转,右括号变左括号) - 按中缀转后缀逻辑处理:
- 扫描
2*(4+3),遇到操作数2先存起来; - 遇到
*,栈空直接入栈; - 遇到
((原右括号),入栈; - 遇到
4存起来,遇到+,栈顶是(,入栈; - 遇到
3存起来,遇到)(原左括号),弹出+与(,此时栈顶是*,弹出*; - 最终临时结果为
2 4 3 + *
- 扫描
- 反转临时结果:
* + 4 3 2(即前缀表达式)
口诀:倒着看中缀→当后缀处理→结果再倒过来
5.2 前缀转中缀:包裹法(像包饺子一样层层嵌套)
核心思路:从左到右扫描,遇到运算符就把后面两个操作数用括号包起来。
案例:前缀表达式 + * 3 4 5 转中缀
分步拆解(每次遇到运算符就"包一层"):
- 扫描第一个运算符
+:后面需要两个操作数,先找后面的元素; - 遇到
*:再找两个操作数3和4,组成(3*4); - 遇到
5:此时+需要的两个操作数已齐,将(3*4)和5用+连接,组成((3*4)+5); - 最终中缀表达式:
(3*4)+5
可视化过程:
+ * 3 4 5 → + (3*4) 5 → (3*4)+5
↑ ↑↑ ↑ ↑ ↑
运算符 操作数对 包裹第一层 最终结果
5.3 中缀转后缀:栈式分拣法(像快递分拣一样按优先级入栈)
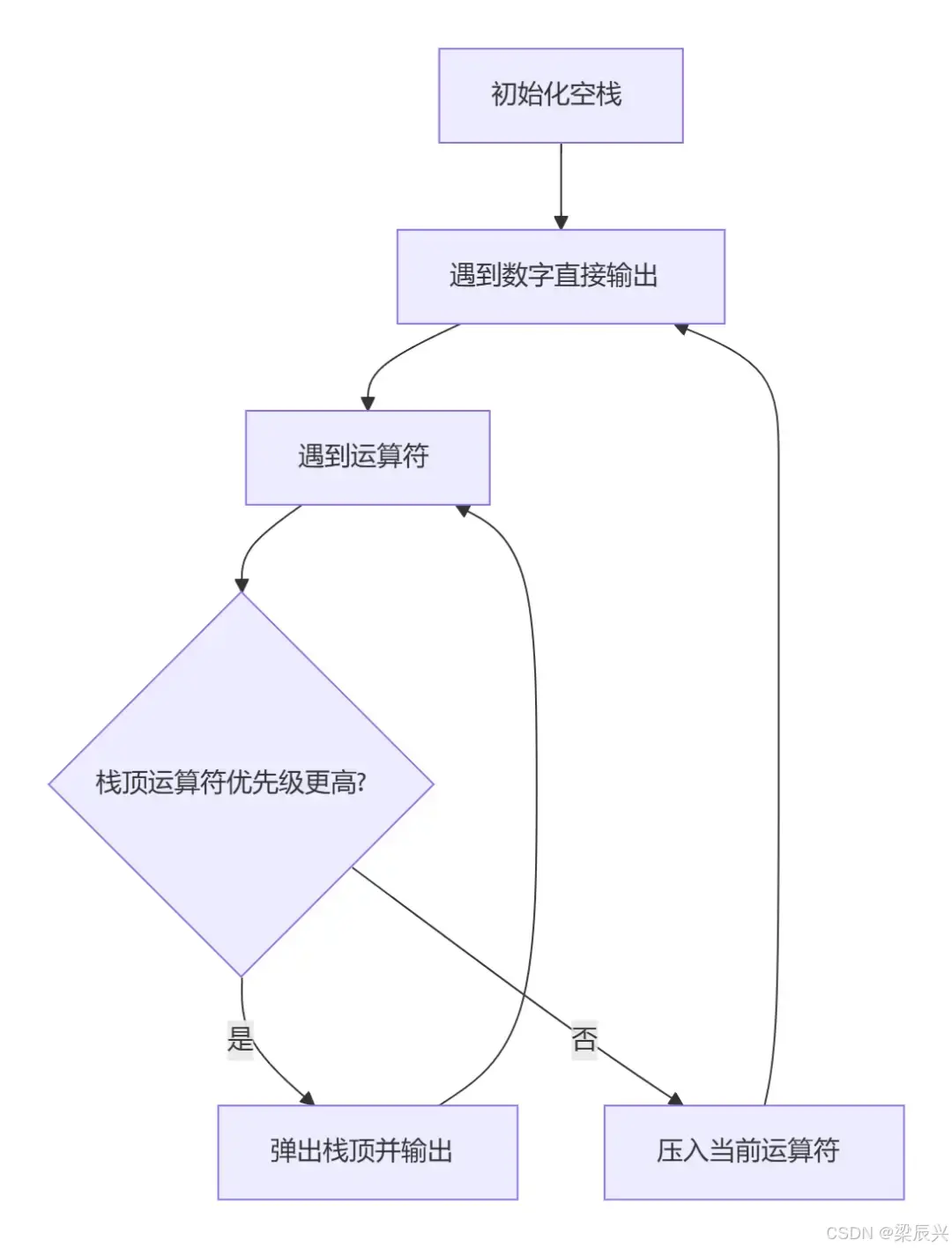
核心思路:用栈存储运算符,遇到操作数直接扔出去,遇到运算符就和栈顶比优先级。
案例:中缀表达式 3+4*2/(1-5) 转后缀
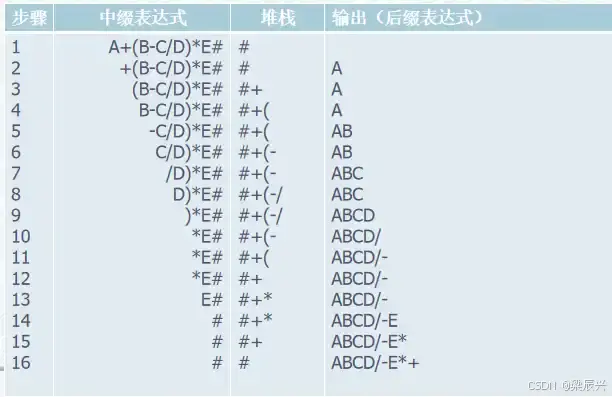
分步拆解(以快递分拣为例,优先级高的快递先出库):
- 扫描
3:操作数,直接存到结果→[3] - 扫描
+:栈空,入栈→栈[+] - 扫描
4:操作数,存结果→[3,4] - 扫描
*:优先级高于栈顶+,入栈→栈[+,*] - 扫描
2:操作数,存结果→[3,4,2] - 扫描
/:优先级等于*,弹出*存结果→[3,4,2,*],然后/入栈→栈[+,/] - 扫描
(:直接入栈→栈[+,/,(] - 扫描
1:操作数,存结果→[3,4,2,*,1] - 扫描
-:栈顶是(,入栈→栈[+,/,(,-] - 扫描
5:操作数,存结果→[3,4,2,*,1,5] - 扫描
):弹出栈中运算符直到(,弹出-存结果→[3,4,2,*,1,5,-],(出栈 - 扫描结束:弹出栈中剩余运算符
/和+,存结果→[3,4,2,*,1,5,-,/,+] - 后缀表达式:
3 4 2 * 1 5 - / +
动画演示逻辑:
中缀:3 + 4 * 2 / (1 - 5)
后缀:3 4 2 * 1 5 - / +
5.4 后缀转前缀:逆序栈法(倒着扫描后缀表达式)
核心思路:倒着看后缀表达式,用栈存操作数,遇到运算符就弹出两个操作数组合。
案例:后缀表达式 3 4 2 * 1 5 - / + 转前缀
分步拆解(倒着走后缀,像拼积木一样组合):
- 倒序扫描后缀:
+ / - 5 1 * 2 4 3 - 初始化空栈,遇到操作数
3、4、2先入栈→栈[3,4,2] - 遇到
*:弹出2和4,组合成*42,入栈→栈[3,*42] - **遇到
1、5入栈→栈[3,*42,1,5] - 遇到
-:弹出5和1,组合成-15,入栈→栈[3,*42,-15] - 遇到
/:弹出-15和*42,组合成/*42-15,入栈→栈[3,/*42-15] - 遇到
+:弹出/*42-15和3,组合成+3/*42-15,入栈→栈[+3/*42-15] - 最终前缀表达式:
+ 3 / * 4 2 - 1 5(格式化后)
关键技巧:
- 倒序扫描时,操作数的顺序要对调(如后缀中
a b +倒序后是+ b a) - 每一步组合的字符串保持运算符在前,操作数在后
🧩 转换方法对比表
| 转换类型 | 核心工具 | 关键步骤 | 案例(以3+4*2为例) |
|---|---|---|---|
| 中缀→前缀 | 栈+反转 | 反转中缀→按中缀转后缀处理→结果反转 | 中缀(3+4)*2→前缀*+342 |
| 前缀→中缀 | 栈+包裹 | 从左到右扫描,遇到运算符就包裹后面两个操作数 | 前缀+*342→中缀(3*4)+2 |
| 中缀→后缀 | 栈+优先级 | 操作数直接存,运算符按优先级入栈弹出 | 中缀3+4*2→后缀342*+ |
| 后缀→前缀 | 栈+逆序 | 倒序扫描后缀,操作数入栈,运算符弹出组合成新字符串 | 后缀342*+→前缀+*342 |
六、表达式处理的应用场景
6.1 计算器实现
- 简单计算器通常使用中缀表达式处理
- 科学计算器可能支持后缀或前缀表达式
- 编程实现计算器时,通常先将中缀表达式转换为后缀表达式,再进行求值

6.2 编译器设计
- 表达式的解析是编译器前端的重要组成部分
- 后缀表达式常用于中间代码生成
- 运算符优先级和结合性的处理是表达式解析的关键
6.3 数据结构教学
- 表达式处理是栈应用的经典案例
- 三种表达式的转换和求值是数据结构课程的重要内容
- 有助于理解栈的特性和应用场景























 2081
2081

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










