Miller effect—improved model in high frequency（Ⅱ）

采用Miller近似可以帮助我们迅速估计主极点的位置，但是在高频条件下该模型则会引入很多误差，这主要是因为放大器增益会受输出节点的电容影响而随频率变化。

因此我们需要找到一个更精确的模型来模拟放大器的高频表现，从而来更好地设计相关参数。

---

1.频响分析

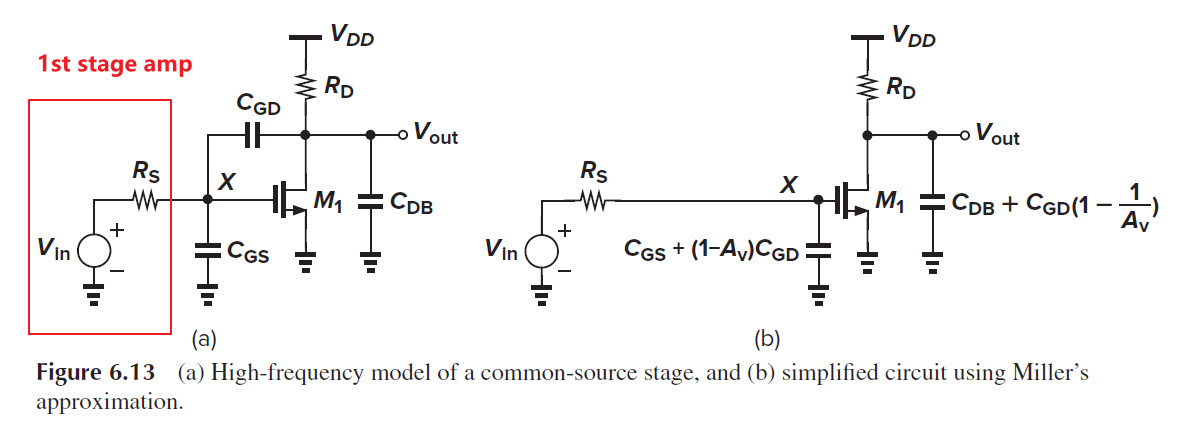
以一个共源极放大器为例，其中Rs模拟上一级放大器的输出阻抗。右图为miller近似的小信号电路。

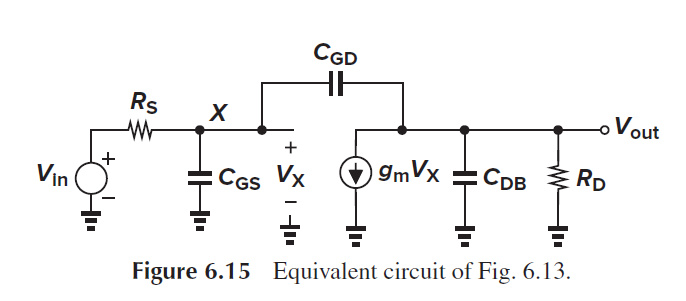
共源极的完整小信号模型。

通过对比两者的传输函数可发现，采用miller近似模型计算的传输函数不仅漏了一个零点，在预测输出极点上也有偏差。

2.改进模型

可通过二端口网络等效来量化miller效应对前后级的影响。

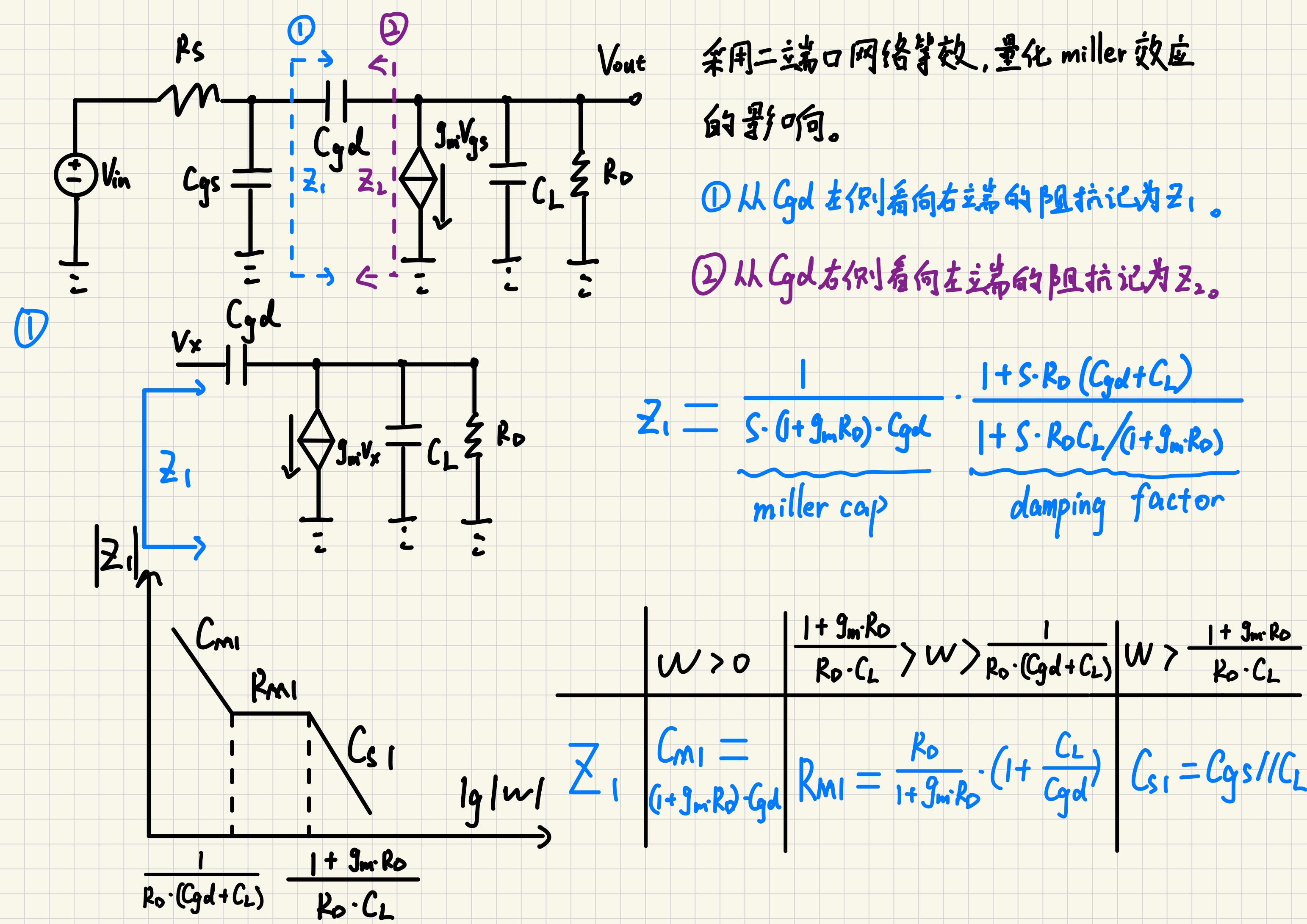
先分析从Cgd左端看向右端的等效阻抗Z1。

由上图计算结果可知，第一节所使用的miller近似仅仅在较低频率时有效，这也解释了其预测主极点较准确的原因。

随着频率不断升高，Z1会先后等效为电容Cm1，电阻Rm1以及电容Cs1。

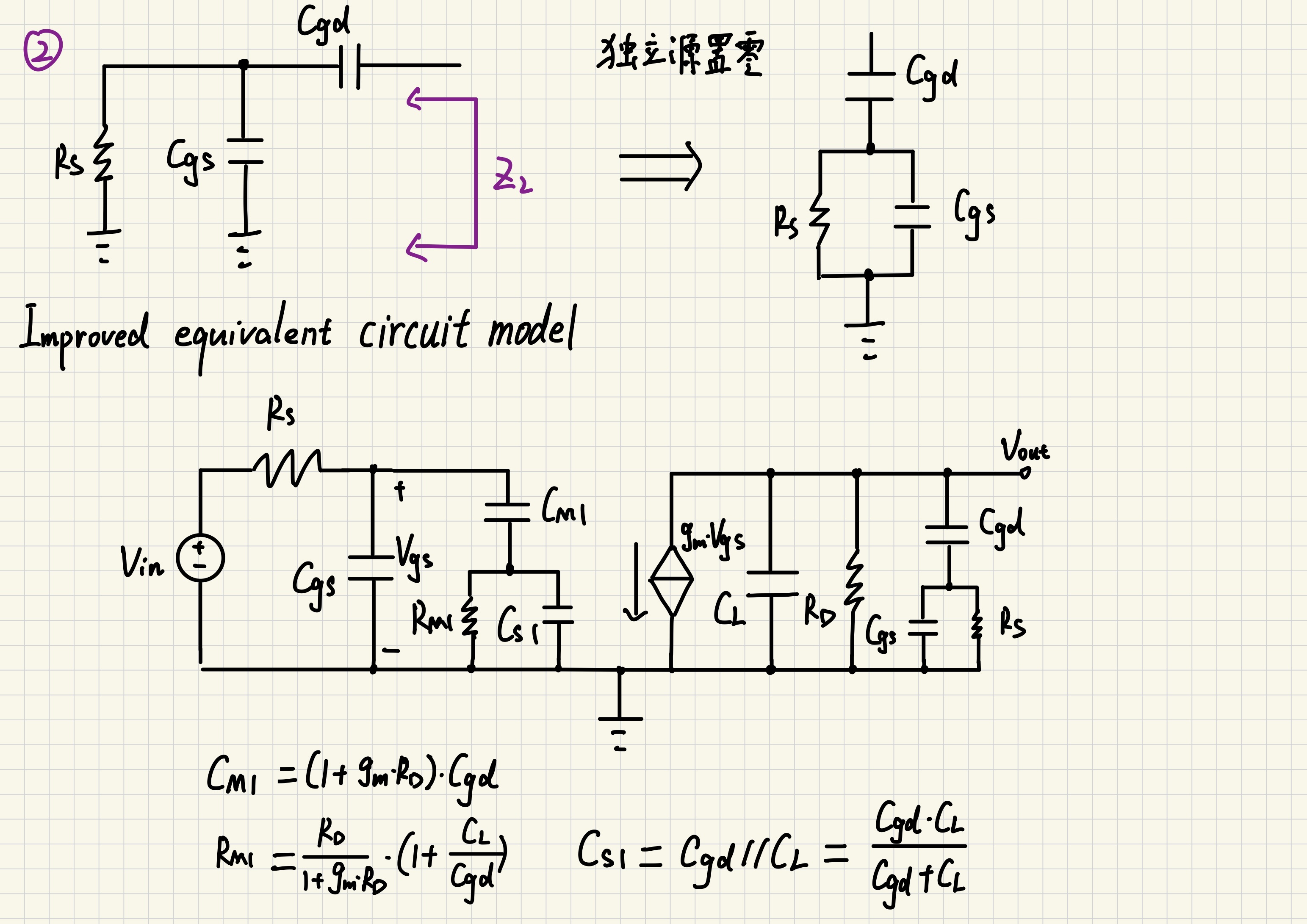
Z2的分析较为简单，只需把输入源Vin置零即可。

然后我们就得到一个升级版的小信号miller效应等效电路。

接下来将通过仿真来验证这个模型的准确性。需要注意该模型依旧缺少一个零点，这是因为该零点频率通常较高，在单位增益带宽积附近，所以这里忽略。

3.仿真验证

3.1仿真设置

3.1.1 Original model

	1st Stage	2nd Stage
gm(uS)	87.60	266.00
C(pF)	0.59	10.28
R(KΩ)	866.55	197.63
Cgd（fF）	20.80

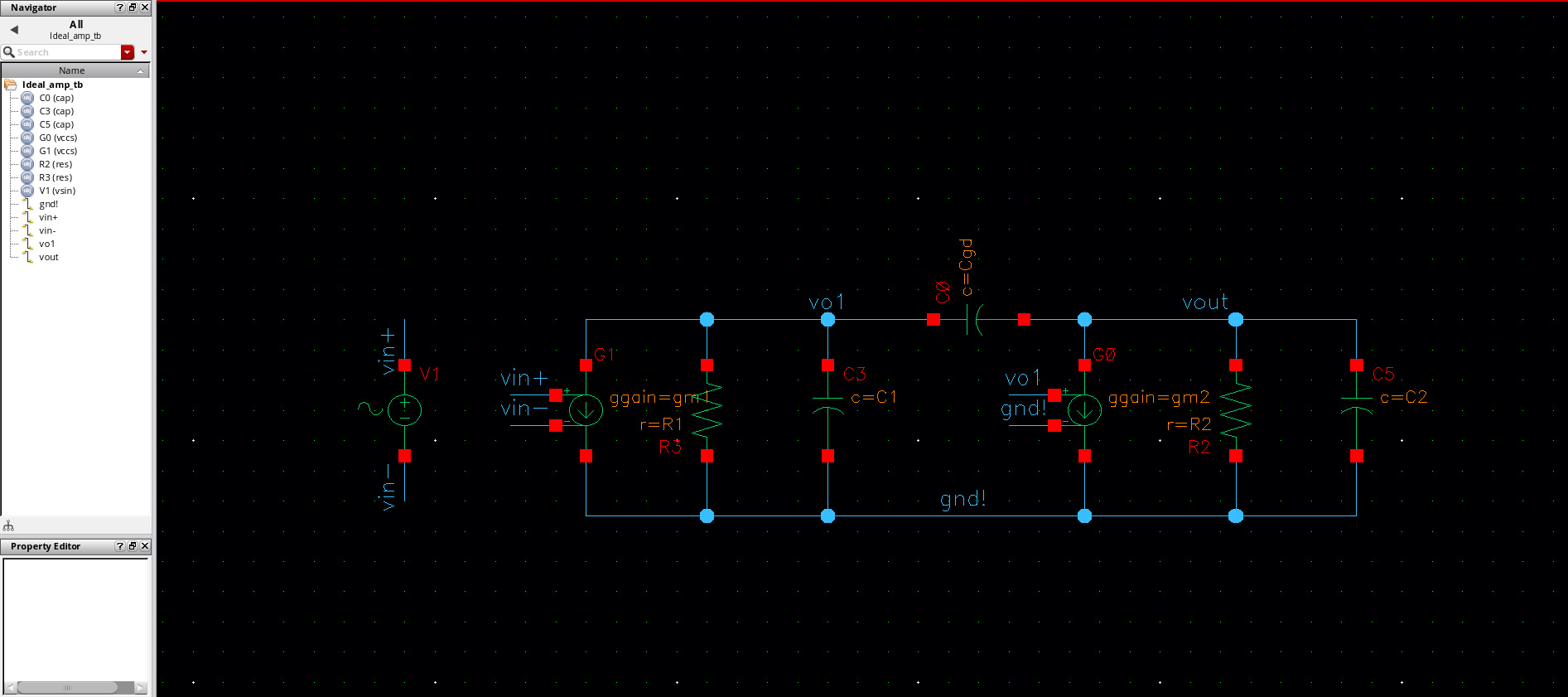
注意这里使用诺顿等效将第一级电压源转变为等效的电流源。

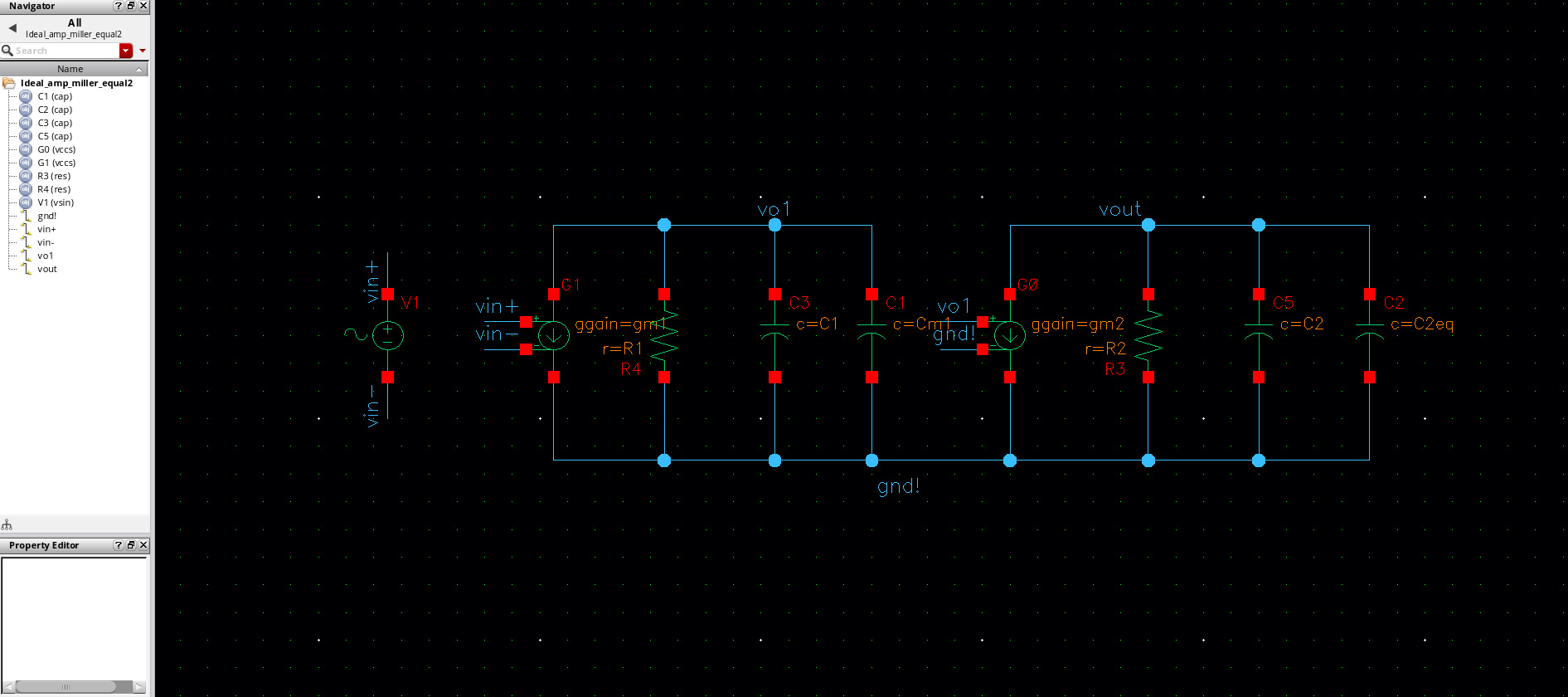
3.1.2 Miller approx. model

Cm1(pF)	C2,equal(pF)
1.1	0.02

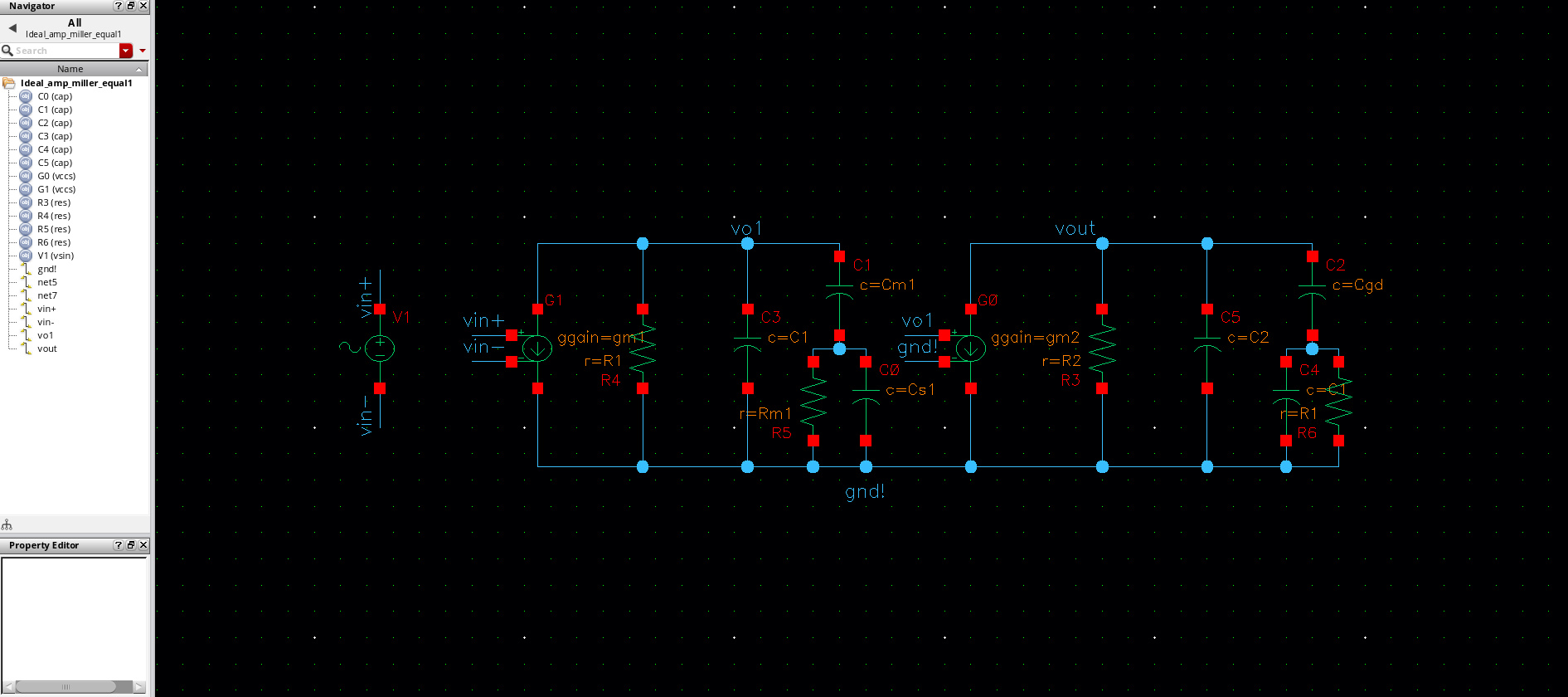
3.1.3 Improved miller model

Cm1(pF)	Rm1(KΩ)	Cs1(pF)
1.1	1825	0.02

3.2仿真波形

仿真结果总结

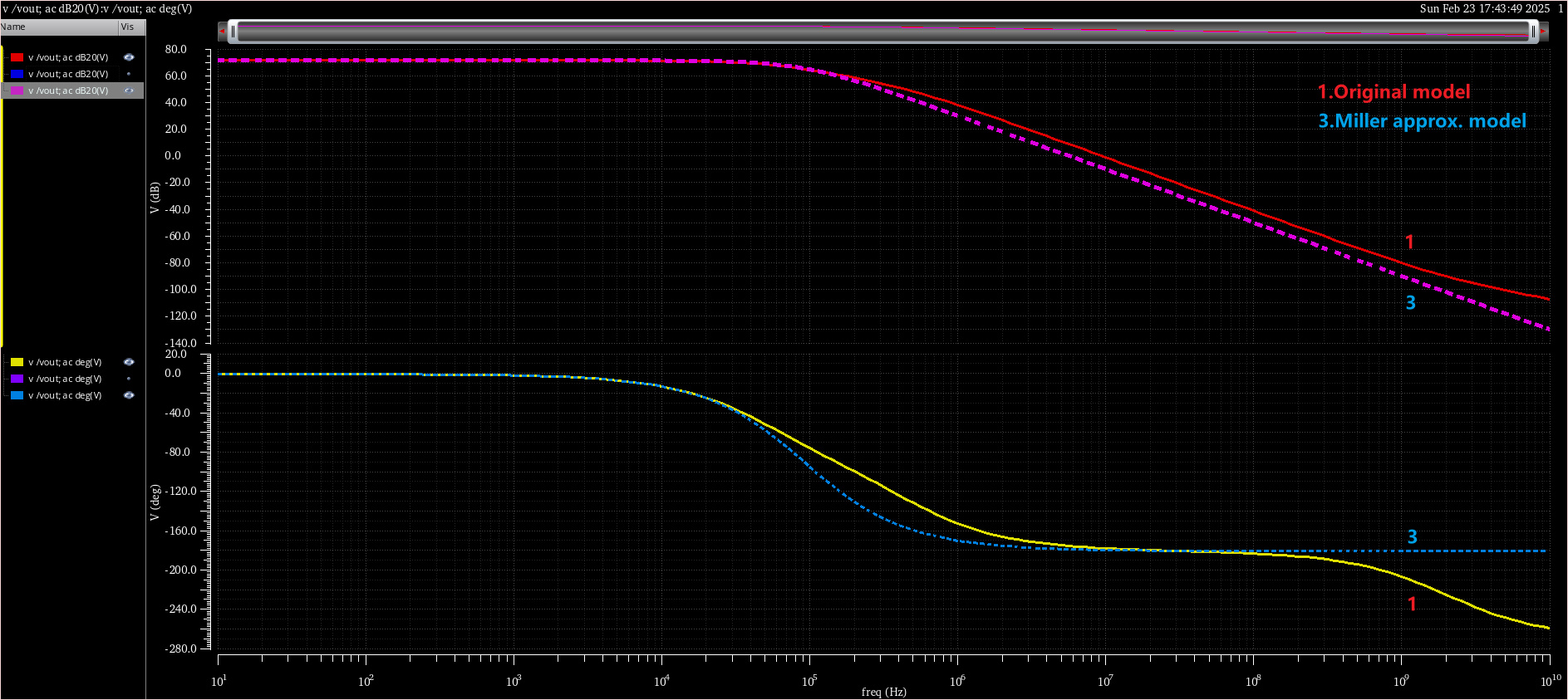
3.2.1对照组——Miller approx. model VS Original model

3.2.2实验组——Improved miller model VS Original model

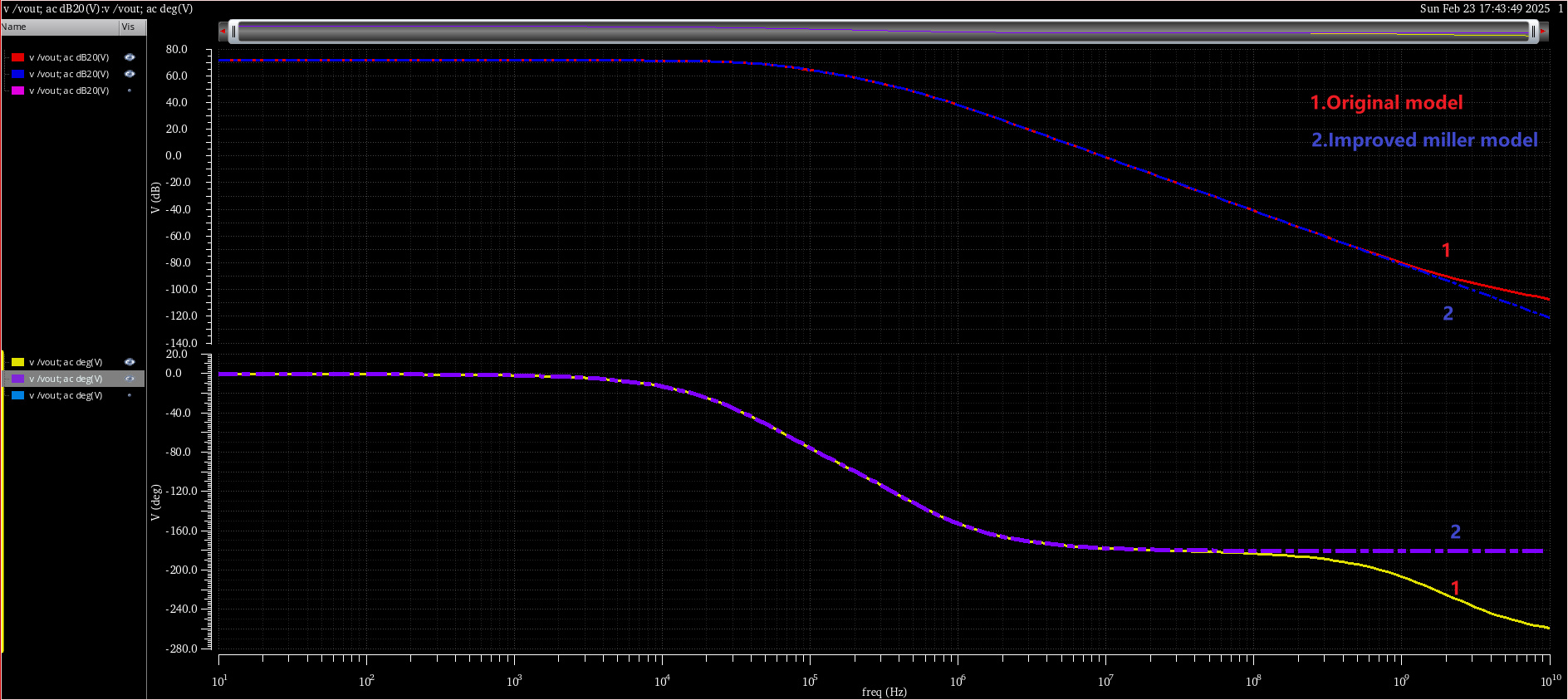
结果显而易见，采用第二节的改进模型更加符合原始电路的频率响应。

3.2.3总结

1）改进miller等效模型在高频响应上比miller近似模型更准确；

2）可根据所关心的频率范围来适当选择等效阻抗，如中频时可用电阻Rm1来表示。

4.参考资料

1.B.Razavi,Design of Analog CMOS Integrated Circuits,2nd ed.

2.H.C.Yang and D.J.Allstot,"Considerations for fast settling operational amplifiers".