Miller effect—通过split-cap和反馈理解（Ⅰ）

1.split-cap法

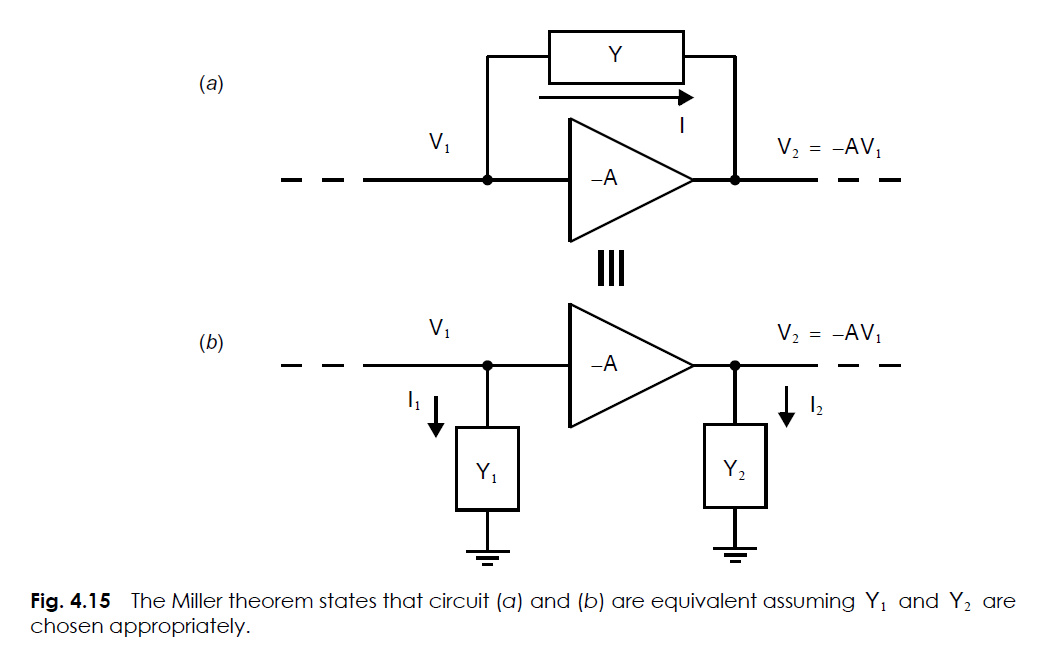
因为处于反向放大状态，故输入V1和输出V2必然异号，满足一正一负。

阻抗Y跨接在反向放大器两端，可推理出当电势沿着阻抗Y所在支路连续变化时，必存在一点Vx＝0。

在前面假设前提下，我们可以将阻抗分为Z1和Z2两部分，当中电位Vx为零电势点。

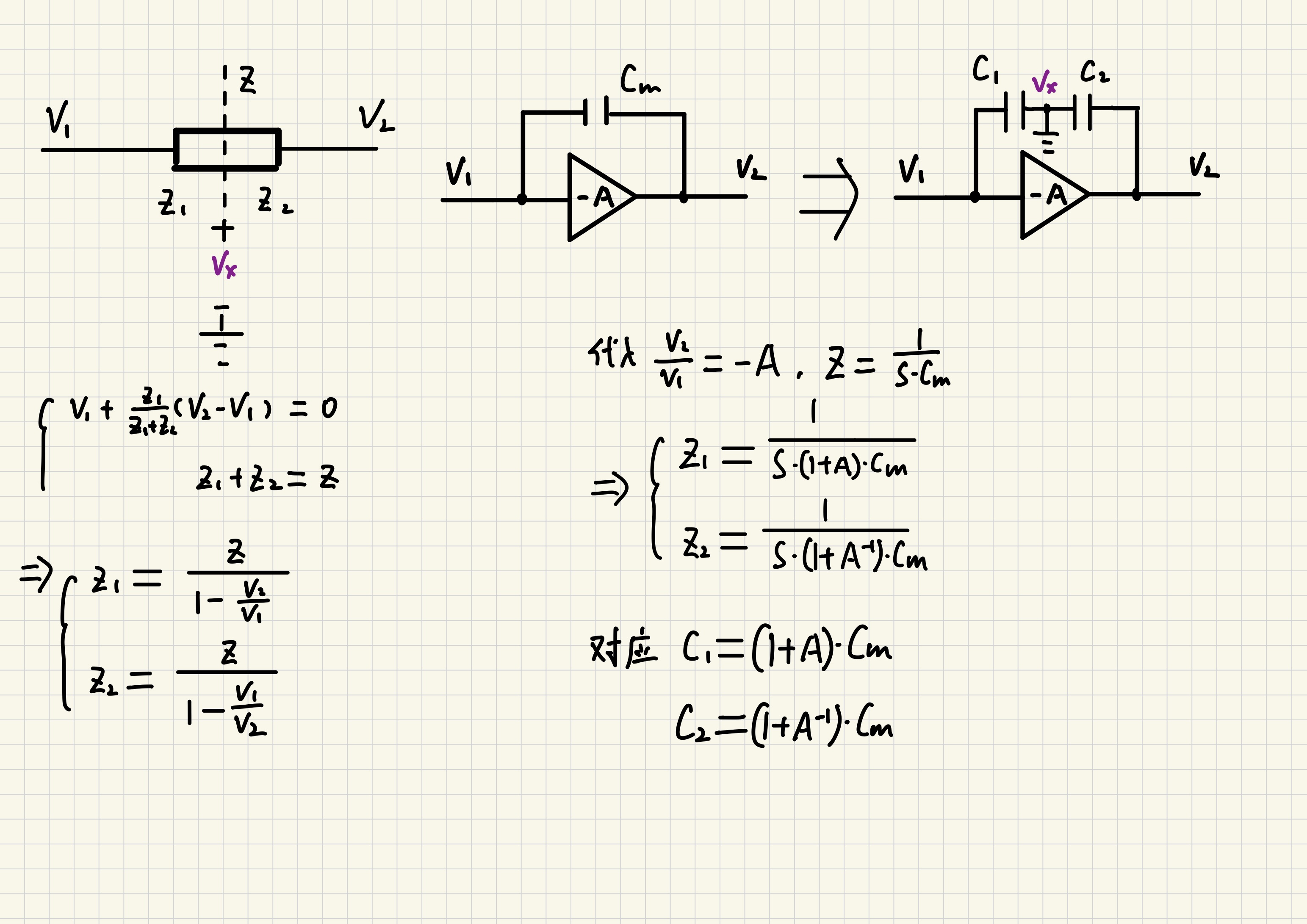
根据上图的计算结果，将电容的阻抗表达式带入阻抗Z1和Z2，便可分别求得输入和输出端对应的等效对地电容C1和C2。

2.反馈角度

站在反馈的角度，miller效应（如图一）本质上属于shunt-shunt型反馈，该类型反馈同时减小输入和输出阻抗。

根据输入阻抗公式

Zin=Z/（1+T）。

以及开环阻抗Z=1/sc，和环路增益T=A。

容易证明

C1=（1+A）*Cm。

那接着怎么去理解等效输出阻抗的变化呢，这就需要画出完整的反馈框图来分析。

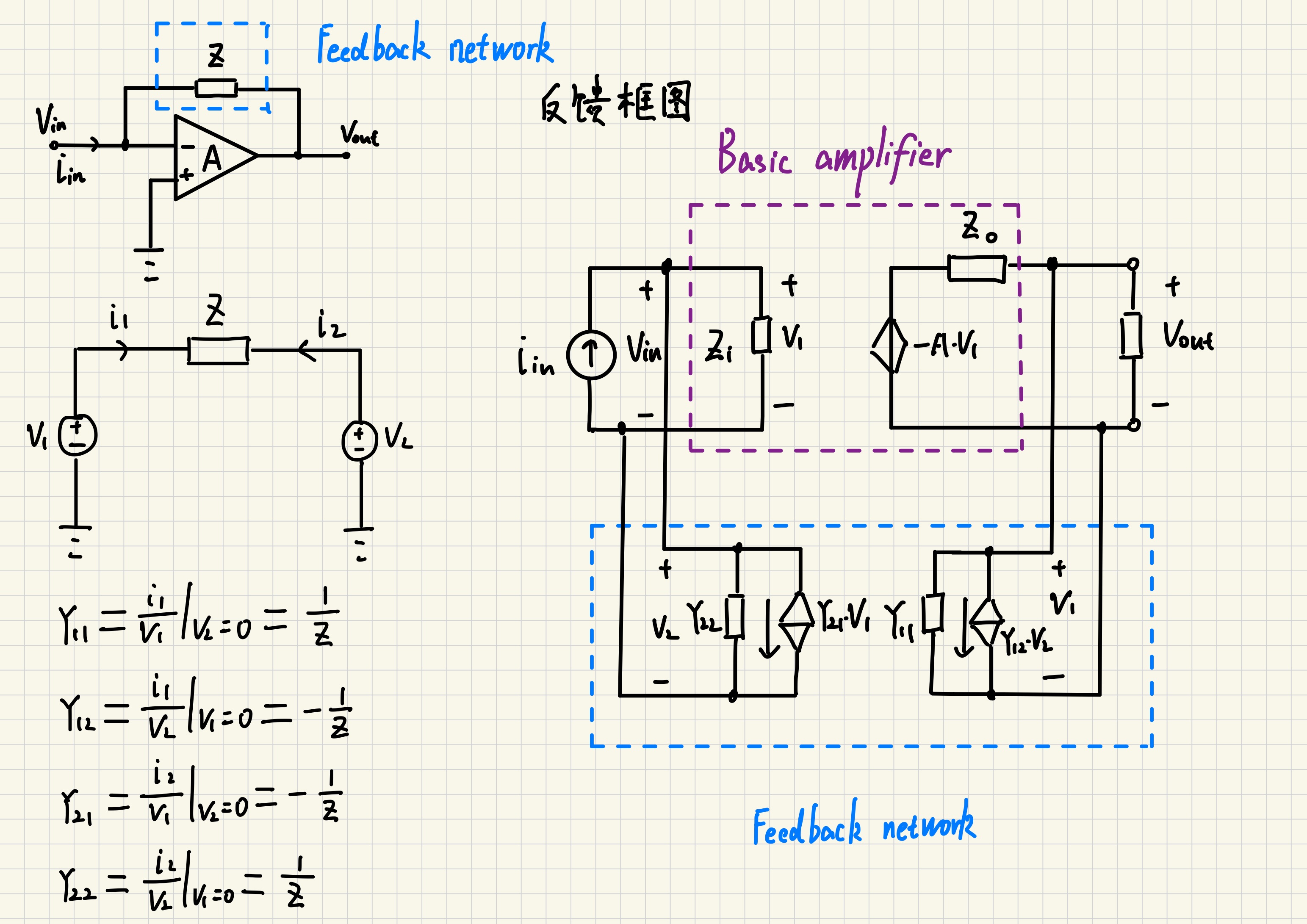
注意上图忽略了放大网络内部的反馈，但考虑了输入信号通过反馈网络产生的前馈信号Y12*V2。

后续会解释为什么。

将上图计算所得Y模型参数代入，得

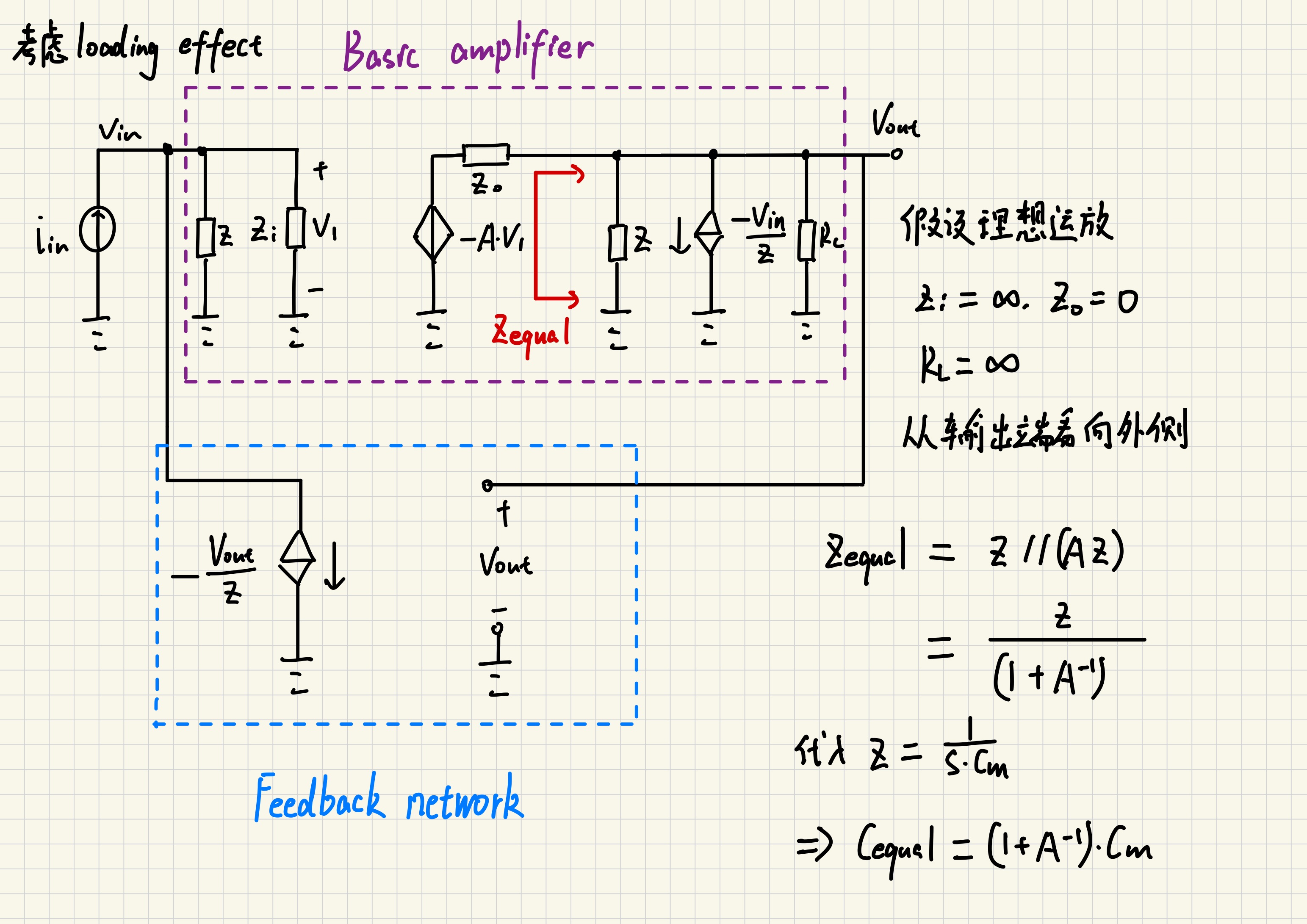
我们首先要明确一个概念，在讨论miller效应时所说的等效输出阻抗应指的是从放大器输出端看向地的等效阻抗（简单讲就是不包括放大器内阻），而不是通常讨论反馈所说的从外部输出端看向内部（考虑运放内阻）。

明确之后，易求得等效输出电容Cequal和方法一结果相同。

将反馈效果总结为以下几点：

1）Vout通过反馈网络到Vin的shunt电流使得等效输入电容变为（1+A）倍；

2）Vin通过反馈网络到Vout的shunt电流也影响了等效输出电容；

3）反馈环路并不一定单向。

3.参考资料

1.K.W.Martin,Analog integrated Circuit Design,2nd ed.