【模电】【补充】RC移相式振荡电路进阶分析

1.为什么选择三阶RC级联

已知一阶RC最多引入90°超前相位，为了达到180°的移相目标，那么先考虑以下三个选项

1）两个RC级联，每级贡献90°超前相位

2）三个RC级联，每级贡献60°超前相位

3）四个RC级联，每级贡献45°超前相位

问题来了，为什么要选择三阶，而不是二或者四？
可从以下两个角度解释：

1）选频特性

2）Loading effect

1.1选频特性

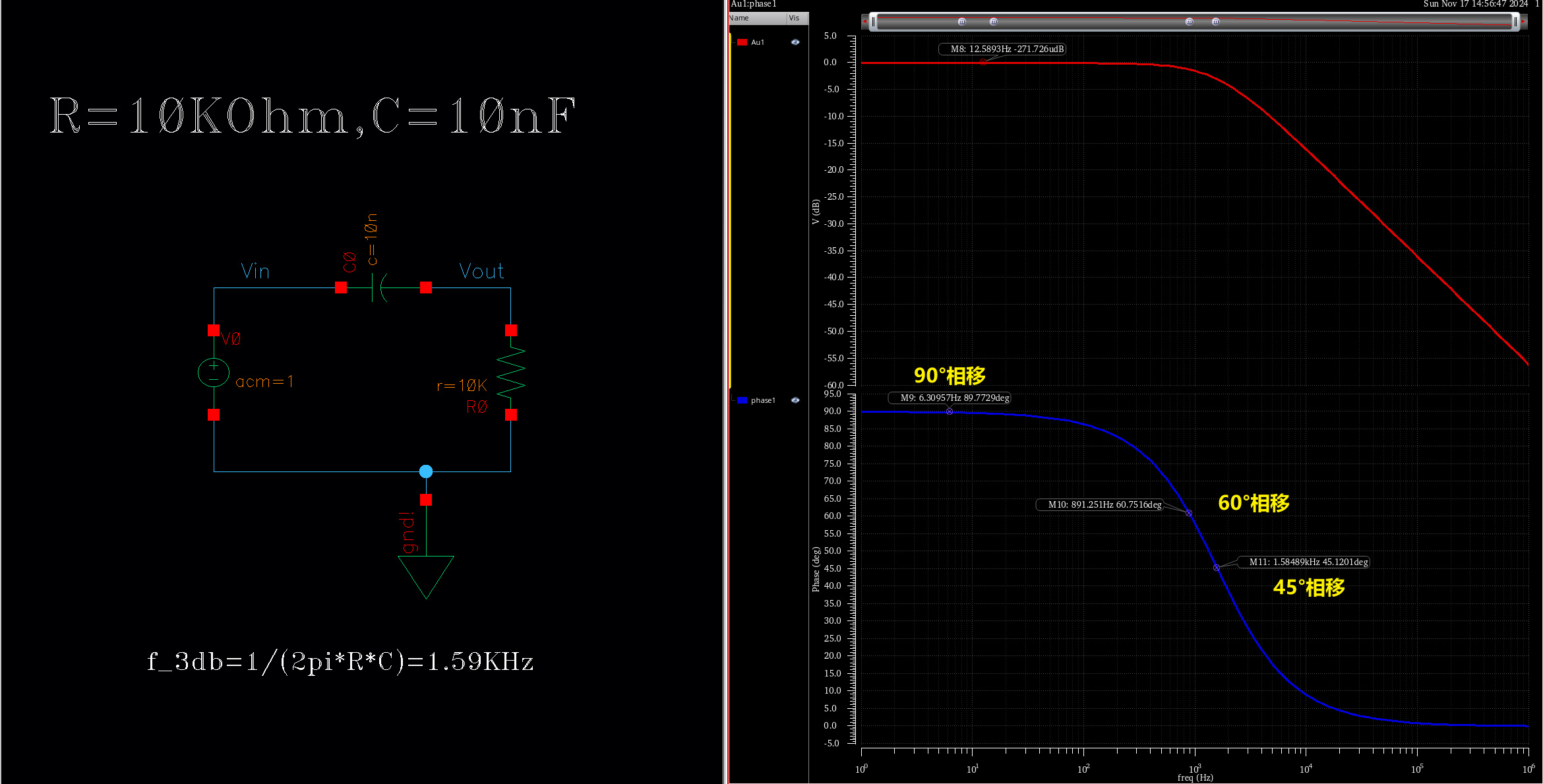
由RC高通滤波器的bode图可看出，相位响应曲线在 90° 及以上时非常平坦，可认为频率的任何漂移对产生的 180° 相移几乎没有影响。

如果由于温度变化而导致振荡器的频率发生变化，相移量几乎不会有任何变化，因此频率稳定性会很差。即使频率在振荡频率附近发生改变，总体相位还是满足360°，最终影响输出波形。

在 60° 或 45° 时，相位响应曲线要陡峭得多。因此，使用三个滤波器每个产生 60°，或四个滤波器每个提供 45°以达到所需的 180°相移，会使频率稳定性更高。

所以pass掉2阶。

那按照同样标准，四阶要比三阶的频率稳定性更好，又为什么不选四阶呢？

主要是因为Loading effect。

1.2Loading effect

以三阶RC为例，若按照每级RC贡献60°相位计算，为什么震荡频率不是

而是

已知N阶RC移相式振荡电路的振荡频率为

（公式推导见参考资料2）

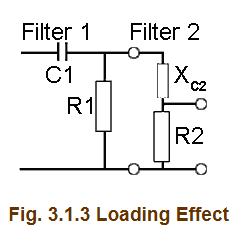
因为考虑实际情况，我们并不能简单粗暴的把三阶看成三个一阶RC级联，因为每一阶的负载都会影响前一阶，这个效应就是loading effect。

为了减轻后级负载对前级产生的loading effect，可以在每级滤波器之间加一个buffer。

下面以二阶RC高通滤波级联为例，通过仿真直观对比插入buffer后的效果。

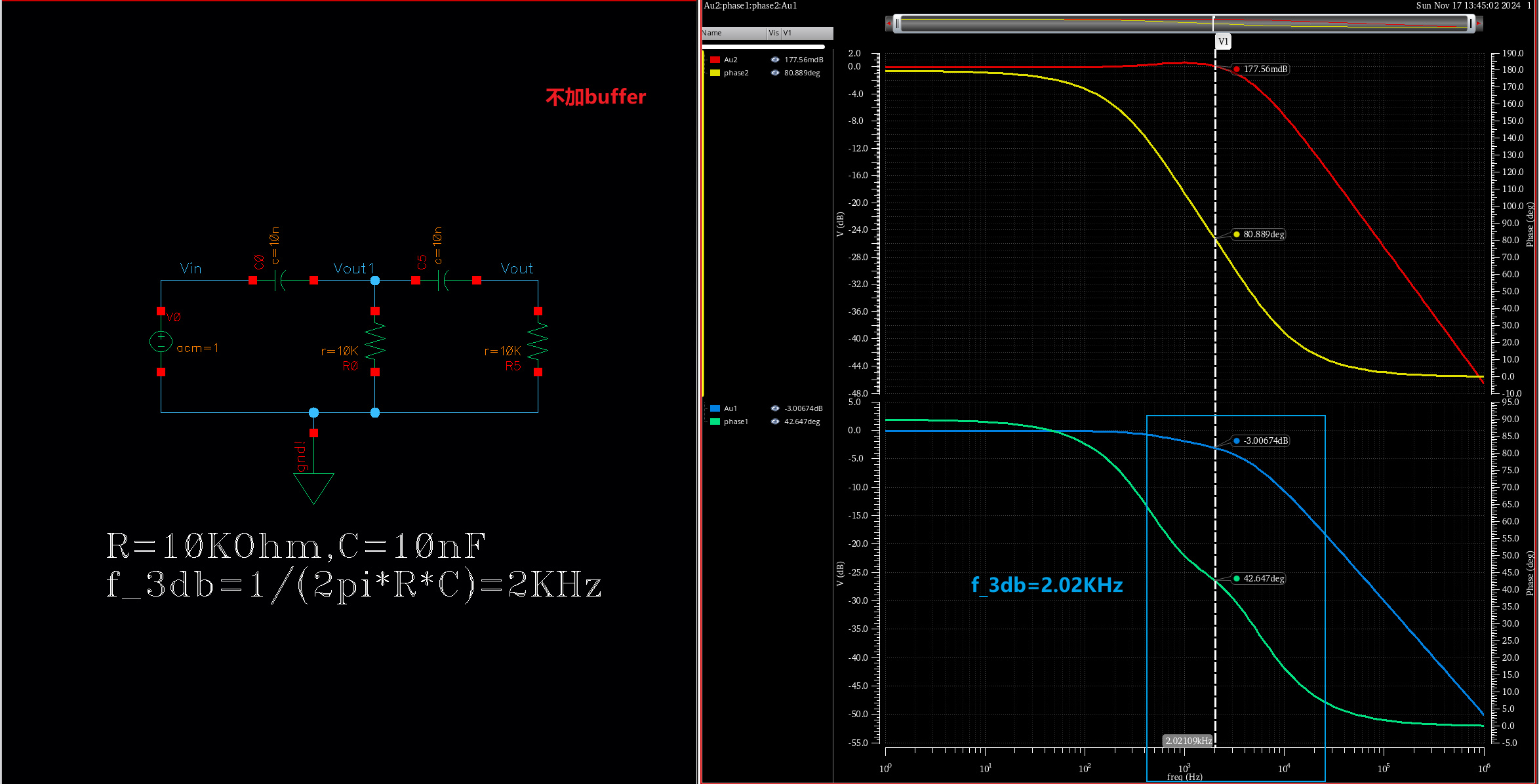
显然，buffer可有效减轻后级负载带来的loading effect。

综上，考虑多阶RC级联带来的loading effect和更复杂的影响，三阶成为了更普遍的选择，同时选用输入内阻更高的CMOS运算放大器会比BJT型更好。

2.更好的选择

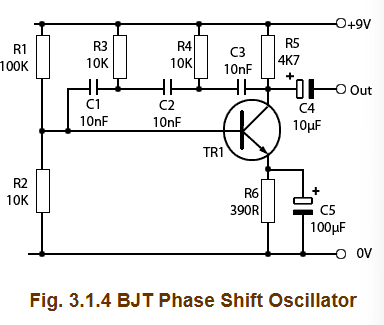
基于RC移相原理，我们可以搭出一个最基本的BJT移相式振荡器。它主要有以下缺点

Cons：

1）波形幅度稳定性不好。若没有附加电路，则无法保证良好的输出波形；

2）频率不易调节。因为调节频率需要组合 3 个可变电容或 3 个大型可变电阻，而这些组件并不容易获得。

那么如何对电路进一步改进呢？

2.1 Phase lead和Phase lag

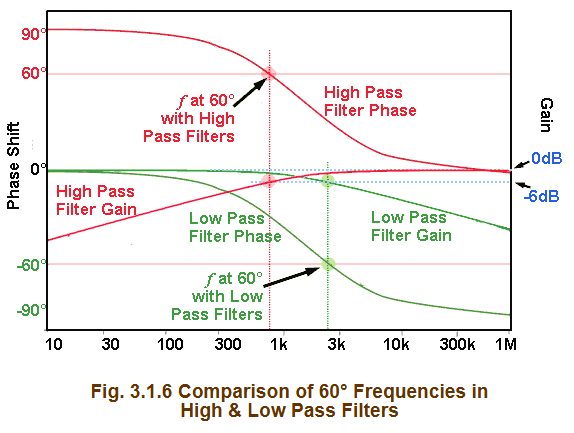
根据上图的RC低通滤波器和高通滤波器bode图对比，在同样R和C参数下，选择RC低通可以实现更高的振荡频率（即Phase lag）。

2.2 Buffered Oscillator

可通过在每级RC后增加一个buffer来减轻loading effect。

每级RC贡献60°相位差，振荡频率为

同时每级贡献-6dB增益衰减，三级总增益衰减约为-18dB（≈1/7.9）。为保证起振，选择放大器增益略大于7.9倍。

3.Reference

1.RC Phase Shift Oscillators

2.https://electronics.stackexchange.com/questions/663656/transfer-function-of-rc-circuit-and-phase-shift/663675#663675

3.RC Phase Shift Oscillator Design for Sine Wave Generation