目录
例题 POJ 1163 数字三角形

方法一 :递归(耗时
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
const int N=1e7+10;
int MAXsum(int i,int j);
int n;int a[MAX][MAX];
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
cout<<MAXsum(1,1);
return 0;
}
int MAXsum(int i,int j)
{
if(i==n)
return a[i][j];
else
{
int x=MAXsum(i+1,j);
int y=MAXsum(i+1,j+1);
return max(x,y)+a[i][j];
}
}方法二:记忆递归
方法一之所以耗时是因为递归出现了重复调用,计算。导致效率低下。所以我们采用一种办法,就是计算过的位置不再计算,将其记住,需要的时候直接调用。
这里使用一个maxsum数组来记录每次计算的结果
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
const int N=1e7+10;
int MAXsum(int i,int j);
int n;int a[MAX][MAX];
int maxsum[MAX][MAX];
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
cin>>a[i][j];
maxsum[i][j]=-1;//-1代表还没计算
}
}
cout<<MAXsum(1,1);
return 0;
}
int MAXsum(int i,int j)
{
if(maxsum[i][j]!=-1)//检测到不等于-1说明该位置计算过了
return maxsum[i][j];
else if(i==n)
maxsum[i][j]= a[i][j];
else
{
int x=MAXsum(i+1,j);
int y=MAXsum(i+1,j+1);
maxsum[i][j] = max(x,y)+a[i][j];
}
return maxsum[i][j];
}方法三:递推(递归的逆运算
我们可以直接用双循环,从数据的底部向上地推出每一个数的MaxSum,这样也能避免递归的重复计算
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 101
const int N=1e7+10;
int n;int a[MAX][MAX];
int maxsum[MAX][MAX];
int main()
{
cin>>n;
int i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=i;j++)
{
cin>>a[i][j];
}
}
for(i=n,j=0;j<=n;j++)
{
maxsum[i][j]=a[i][j];
}
for(i=n-1;i>=1;i--)
{
for(j=1;j<=i;j++)
{
maxsum[i][j]=max(maxsum[i+1][j],maxsum[i+1][j+1])+a[i][j];//从下到上进行递推合并
}
}
cout<<maxsum[1][1];
return 0;
}总结 动态规划解题一般思路:
1.将原问题分解为子问题(分治思想)
1.把原问题分解为若干个子问题,子问题和原问题相同或类似,通过逐步分解的办法使得原问题规模变小到可以直接解决出子问题,原问题便得到了解决。(在数在三角形中分解到数字三角形的底边,便得到答案了)
2.子问题一旦求出,便被保存,避免再次重复计算,所以每个子问题都只需求一次。(可以用数组保存每次求解子问题的答案)
2.确定状态
所有状态的集合,构成问题的 状态空间 ,状态空间 的大小与动态规划解决问题的时间直接相关。与子问题相关的各个变量的一组取值,称之为一个状态,同样一个状态对应于一个或多个子问题。而某个状态的值一旦确定,那么该子问题便得到了解决。
我们通常创立一个数组来存放该状态下的值,该值不一定是一个整数或浮点数,可能是需要一个结构才能表示,那么该数组可以是结构体数组。一个状态下的值可以是一个或多个子问题的解
(数字三角形里共有n(n+1)/2个数据,则对应有这么多状态,确定了每个状态的值,问题便得到了解决)
3.确定一些初始状态(边界状态)的值
比如 ”数字三角形“,我们确定的初始状态就是底边的一行数据,而其对应的值就是底边数字本身。然后由已知推未知。
4.确定状态转移方程
定义出了状态,以及在该状态下的值以后,我们要找出不同状态之间要如何迁移。即从一个或多个已知值的状态找出另一个状态的值,那么我们就需要它们之间的关系式,递推公式,也称作”状态转移方程“。类似于小学所讲的应用题,由题 目找出数据之间的关系。也就是说,该方程就蕴含在题目当中。
例如例题中数字三角形的状态转移方程就是: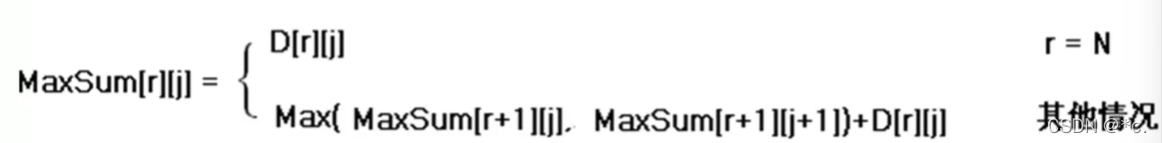
能用动态规划解决问题的特点:
1.问题具有最优子结构的性质
如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质。比如例题中数字三角形 我们求每个状态的值都必须要求用来求它的状态的值是最优的。
2.无后效性
当前状态的值一旦确定,则此后过程的演变就只和这个状态的值有关,和他怎么来的没有任何关系。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








