力扣刷题之数组篇

题号：35、27、977、209、59

2025/2/20

35.搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

算法要求logn，使用二分查找，二分查找使用双指针low和high得到mid，若排序数组中含有想要查找的内容则返回mid,若无则返回low指针所指位置。

class Solution(object):
    def searchInsert(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        low = 0
        high = len(nums) - 1
        while low <= high:
            mid = (low + high) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                low = mid + 1
            else:
                high = mid - 1
        return low

27.移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

• 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
• 返回 k
• 示例 1：

• 输入：nums = [3,2,2,3], val = 3
  输出：2, nums = [2,2,_,_]
  解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
  你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

  示例 2：

  输入：nums = [0,1,2,2,3,0,4,2], val = 2
  输出：5, nums = [0,1,4,0,3,_,_,_]
  解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
  注意这五个元素可以任意顺序返回。
  你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

如果采用删除一个移动一次的方法，程序的复杂度会较高。使用变量h记录数组中与val值相等的元素的个数，将与val值不等的元素向前移动代替val值相等的元素，最后得到的元素个数为原长度-相等的值的个数。

class Solution(object):
    def removeElement(self, nums, val):
        """
        :type nums: List[int]
        :type val: int
        :rtype: int
        """
        length = len(nums)
        i = 0
        h = 0
        while i < length:
            if nums[i] == val:
                h += 1
            else:
                nums[i-h] = nums[i]
            i += 1
        return length - h
        

977.有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

• 请你设计时间复杂度为 O(n) 的算法解决本问题

可将负数看作是一个已排序的序列，将非负数看作是另一个，这样就是两个已排序的序列进行整合，就想到归并排序。负数越小，平方越大，所以负数序列的元素平方大小是从前往后变小；非负数是从前往后增大，则直接将两序列的头尾进行比较，创建一个空白数组，将元素从后往前放。

class Solution(object):
    def sortedSquares(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        length = len(nums)
        ans = [0] * length
        i = 0
        j = length-1
        p = j
        while p >= 0:
            if nums[i]**2 > nums[j]**2:
                ans[p] = nums[i]**2
                i += 1
            else:
                ans[p] = nums[j]**2
                j -= 1
            p -= 1
        return ans

2025/2/21

209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

思考：看到这个题，首先想到的方法是对数组进行排序，先把大的进行相加那么子数组的长度应该能够达到最小，这种方法复杂度较高；看了题解，采用双指针的方法，从左到右不断扩展右节点，删除冗余左节点，使用一个变量对最小长度进行记录。

class Solution(object):
    def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        n = len(nums)
        s = left =0
        ans = n + 1
        for right, x in enumerate(nums):
            s += x
            while (s -nums[left]) >= target:
                s -= nums[left]
                left += 1
            if s >= target:
                ans = min(ans, right - left + 1)
        return ans if ans <= n else 0

59.螺旋矩阵

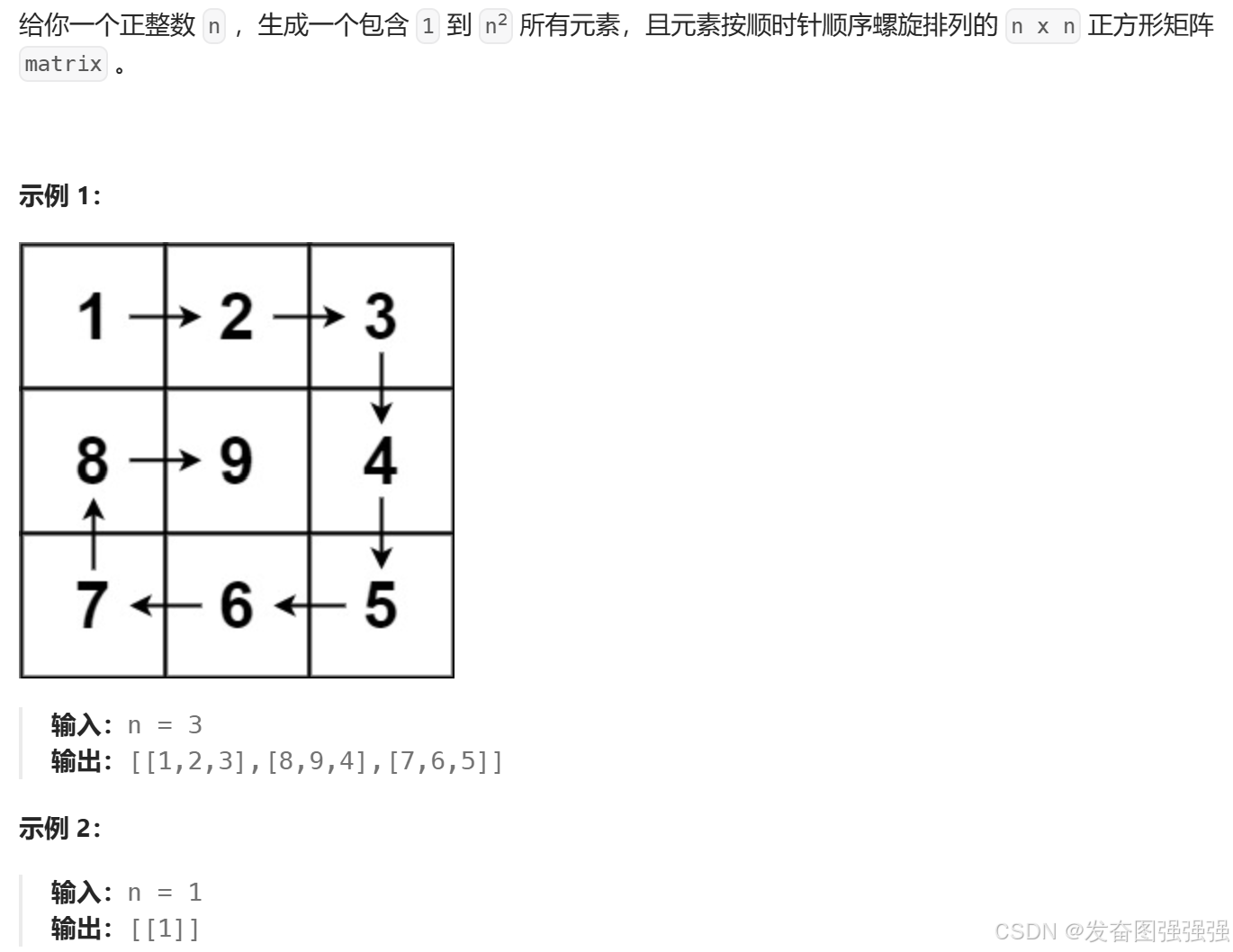
思考：从1-n^2的数的顺序是从左到右，从上往下，从右到左，从下往上，使用四个变量来表示上下左右四个边界，填满一个边界则缩小矩阵，以要填入的数的大小作为迭代条件。

class Solution(object):
    def generateMatrix(self, n):
        """
        :type n: int
        :rtype: List[List[int]]
        """
        sq = [[0 for _ in range(n)] for _ in range(n)]
        if n == 1:
            sq[0][0] = 1
        k = 1
        p = n ** 2
        l = t = 0
        r = b = n - 1
        while k <= p:
            for i in range(l, r + 1, 1):
                sq[t][i] = k
                k += 1
            t += 1
            for i in range(t, b + 1, 1):
                sq[i][r] = k
                k += 1
            r -= 1
            for i in range(r, l - 1, -1):
                sq[b][i] = k
                k += 1
            b -= 1
            for i in range(b, t - 1, -1):
                sq[i][l] = k
                k += 1
            l += 1
        return sq