【约束非线性优化1】投影梯度下降法

1. 投影梯度下降法(PGD)

1.1 介绍

前面章节我们介绍了梯度下降法来解决无约束的非线性优化问题。那么如何解决带约束的非线性优化问题呢？一个直观的想法是：我们依旧先进行梯度下降到一个相对较小的点，然后再将这个点通过某种方式投影到可行域内。如图：

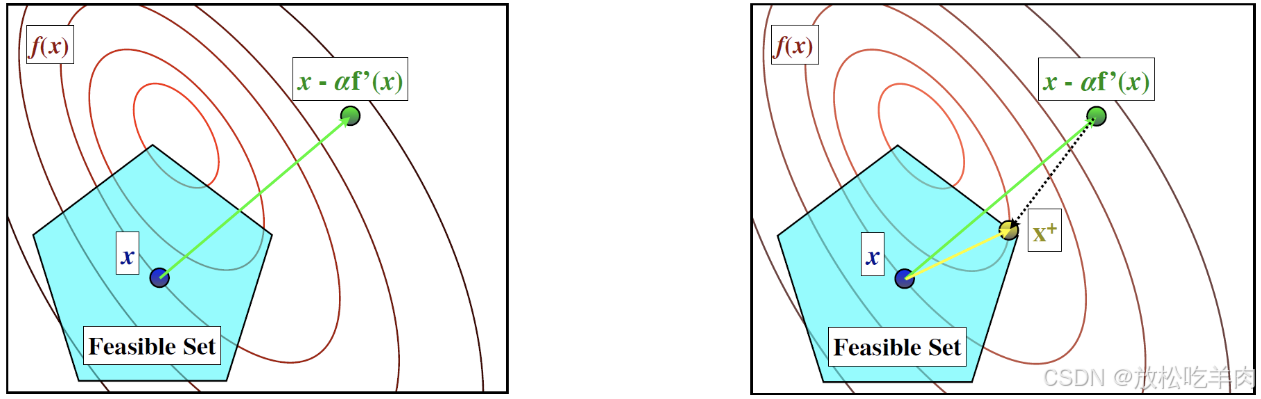
• 第一步：进行无约束的梯度下降：

$${\mathbf{x}}^{k+\frac{1}{2}}={\mathbf{x}}^k-{\eta }_k\nabla f({\mathbf{x}}^k)$$

• 第二步：将 ${\mathbf{x}}^{k+\frac{1}{2}}$ 通过某种度量映射到可行域 $\Omega$ 内最接近的点：

$${\mathbf{x}}^{k+1}\in \arg \underset{\mathbf{x}\in \Omega }{\min }||\mathbf{x}-{\mathbf{x}}^{k+\frac{1}{2}}||$$

记”把 $\mathbf{x}$ 投影到 $\Omega$ 上”为：${\mathcal{P}}_{\Omega }(\mathbf{x})=\arg \underset{{\mathbf{x}}^{\prime }\in \mathbf{\Omega }}{\min }||{\mathbf{x}}^{\prime }-\mathbf{x}||$，对于凸可行域，投影 ${\mathcal{P}}_{\Omega }(\mathbf{x})$ 是唯一的。

1.2 理解

【回忆】：在无约束非线性优化中，梯度下降法可以看成是最小化某个点处的二阶估计：
x k + 1 = arg ⁡ min ⁡ x { f ( x k ) + ∇ f ( x k ) T ( x − x k ) + 1 2 η k ∣ ∣ x − x k ∣ ∣ 2 } . \mathbf{x}^{k+1}=\arg\min\limits_{\mathbf{x}}\{f(\mathbf{x}^k)+\nabla f(\mathbf{x}^k)^T(\mathbf{x}-\mathbf{x}^k)+\frac{1}{2\eta_k}||\mathbf{x}-\mathbf{x}^k||^2\}. xk+1=argxmin​{f(xk)+∇f(xk)T(x−xk)+2ηk​1​∣∣x−xk∣∣2}.
加上约束后，
x k + 1 ∈ arg ⁡ min ⁡ x ∈ Ω { f ( x k ) + ∇ f ( x k ) T ( x − x k ) + 1 2 η k ∣ ∣ x − x k ∣ ∣ 2 } ≡ arg ⁡ min ⁡ x ∈ Ω { η k f ( x k ) ⏟ constant + η k ∇ f ( x k ) T ( x − x k ) + 1 2 ∣ ∣ x − x k ∣ ∣ 2 } (multiply by  η k ) ≡ arg ⁡ min ⁡ x ∈ Ω { η k 2 2 f ( x k ) ⏟ constant + η k ∇ f ( x k ) T ( x − x k ) + 1 2 ∣ ∣ x − x k ∣ ∣ 2 } ( ±  constants not rely on  x ) ≡ arg ⁡ min ⁡ x ∈ Ω { 1 2 ∣ ∣ ( x − x k ) + η k ∇ f ( x k ) ∣ ∣ 2 } ≡ arg ⁡ min ⁡ x ∈ Ω { ∣ ∣ x − ( x k − η k ∇ f ( x k ) ) ⏟ gradient descent ∣ ∣ 2 } . \begin{align} \mathbf{x}^{k+1}&\in\arg\min\limits_{\mathbf{x}\in\Omega}\{f(\mathbf{x}^k)+\nabla f(\mathbf{x}^k)^T(\mathbf{x}-\mathbf{x}^k)+\frac{1}{2\eta_k}||\mathbf{x}-\mathbf{x}^k||^2\}\\ &\equiv \arg\min\limits_{\mathbf{x}\in\Omega}\{\underbrace{\eta_kf(\mathbf{x}^k)}_{\text{constant}}+\eta_k\nabla f(\mathbf{x}^k)^T(\mathbf{x}-\mathbf{x}^k)+\frac{1}{2}||\mathbf{x}-\mathbf{x}^k||^2\} \text{(multiply by $\eta_k$)}\\ &\equiv \arg\min\limits_{\mathbf{x}\in\Omega}\{\underbrace{\frac{\eta_k^2}{2}f(\mathbf{x}^k)}_{\text{constant}}+\eta_k\nabla f(\mathbf{x}^k)^T(\mathbf{x}-\mathbf{x}^k)+\frac{1}{2}||\mathbf{x}-\mathbf{x}^k||^2\} \text{($\pm$ constants not rely on $\mathbf{x}$)}\\ &\equiv \arg\min\limits_{\mathbf{x}\in\Omega}\{\frac{1}{2}||(\mathbf{x}-\mathbf{x^k})+\eta_k\nabla f(\mathbf{x}^k)||^2\}\\ &\equiv \arg\min\limits_{\mathbf{x}\in\Omega}\{||\mathbf{x}-\underbrace{(\mathbf{x}^k-\eta_k\nabla f(\mathbf{x}^k))}_{\text{gradient descent}}||^2\}. \end{align} xk+1​∈argx∈Ωmin​{f(xk)+∇f(xk)T(x−xk)+2ηk​1​∣∣x−xk∣∣2}≡argx∈Ωmin​{constant ηk​f(xk)​​+ηk​∇f(xk)T(x−xk)+21​∣∣x−xk∣∣2}(multiply by ηk​)≡argx∈Ωmin​{constant 2ηk2​​f(xk)​​+ηk​∇f(xk)T(x−xk)+21​∣∣x−xk∣∣2}(± constants not rely on x)≡argx∈Ωmin​{21​∣∣(x−xk)+ηk​∇f(xk)∣∣2}≡argx∈Ωmin​{∣∣x−gradient descent (xk−ηk​∇f(xk))​​∣∣2}.​​

1.3 适用场景

当投影操作计算方便时，即可行域较为简单时可用。以下是一些简单可行域的例子：

• 变量只有上界或下界：$L\le \mathbf{x}\le U$
• 只有线性等式约束：${\mathbf{a}}^T\mathbf{x}=\mathbf{b}$
• 只有半空间约束：${\mathbf{a}}^T\mathbf{x}\le \mathbf{b}$
• 只有 norm-ball 约束：$||\mathbf{x}|{|}_p\le \tau$，for $p=1,2,\infty$

【例1】（使用投影梯度下降解SVM）

【例2】（将 $L_1$ 正则化，i.e.，LASSO回归，转换成约束优化问题）

2. 应用：软间隔支持向量机

2.1 引入松弛变量 ${\xi }_i$

在之前的介绍中，我们假设数据点是能够用一个线性超平面分割的，于是我们形式化求解了硬间隔的SVMs。在实际应用中，我们常常很难遇到能够完全线性分离的数据集，如图：

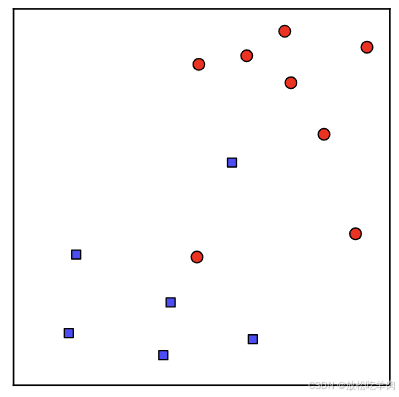
这种情况下，我们就无法找到 $(\mathbf{x},b)$ 满足 $y^i({\mathbf{x}}^T{\mathbf{s}}^i+b)\ge 1,\forall i=1,\cdots ,m$。所以我们试图为每一个训练样本 ${\mathbf{s}}^i$ 引入一个松弛变量 ${\xi }_i\ge 0$ 来放宽原来的约束：
$$y^i({\mathbf{x}}^T{\mathbf{s}}^i+b)\ge 1-{\xi }_i$$
其中，松弛变量 ${\xi }_i\ge 0$ 反应了原训练样本违反原来约束的程度。如果 ${\xi }_i=0$，说明对应的 ${\mathbf{s}}^i$ 能够被 margin 分隔开。如果 ${\xi }_i\ge 1$，则说明 ${\mathbf{s}}^i$ 将会被错误的分类，因为在这个情况下 $y^i({\mathbf{x}}^T{\mathbf{s}}^i+b)$ 可能会变成负数。

因此，我们通过最小化平均松弛变量 $\frac{1}{m}\sum {\xi }_i$ 来使得平均约束违反程度最小。

2.2 用PGD求解软间隔SVM

我们将 $\frac{C}{m}\sum {\xi }_i$ 引入原问题目标函数，其中 $C$ 权衡了 $||\mathbf{x}|{|}^2$ 和 $\sum {\xi }_i$ 。为了简化问题，我们忽略 $\mathbf{b}$，则软间隔的SVM原问题为：
$$\begin{gathered} \underset{\mathbf{x},\xi }{\min }\frac{1}{2}||\mathbf{x}|{|}^2+\frac{C}{m}\sum _{i=1}^m{\xi }_i \\ \text{s.t. }{y}^i({\mathbf{x}}^T{\mathbf{x}}^i)\ge 1-{\xi }_i,{\xi }_i\ge 0,\forall i=1,\cdots ,m \end{gathered}$$
使用 KKT 条件我们可以推导出软间隔SVM对偶问题：
$$\begin{gathered} \underset{\lambda }{\max }\sum _{i=1}^m{\lambda }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\lambda }_i{\lambda }_j{y}^i{y}^j({\mathbf{s}}^i{)}^T{\mathbf{s}}^j \\ \text{s.t. }{\lambda }_i\in [0,C/m],\forall i=1,\cdots ,m \end{gathered}$$
用对偶函数表示为：
$$\begin{gathered} \underset{\lambda }{\max }q(\lambda ):=\sum _{i=1}^m{\lambda }_i-\frac{1}{2}{\lambda }^{T}Q\lambda \\ \text{s.t. }{\lambda }_i\in [0,C/m],\forall i=1,\cdots ,m \\ \text{where }Q:=\left[\begin{array}{ccc}(y^1{)}^2({\mathbf{s}}^1{)}^T{\mathbf{s}}^1& \cdots & y^1{y}^m({\mathbf{s}}^1{)}^T{\mathbf{s}}^m\\ ⋮& \ddots & ⋮\\ y^m{y}^1({\mathbf{s}}^m{)}^T{\mathbf{s}}^1& \cdots & (y^m{)}^2({\mathbf{s}}^m{)}^T{\mathbf{s}}^m\end{array}\right] \end{gathered}$$
接下来对其使用PGD算法：

• step 1：初始化 ${\lambda }_0\in {\mathbb{R}}^m$ 和 $Q$
• step 2：for $k=0,1,\cdots ,t-1$ do
  • step 2.1：${\lambda }_{k+\frac{1}{2}}={\lambda }_k-{\eta }_k\nabla q({\lambda }_k)$
  • step 2.2： λ k + 1 = min ⁡ { max ⁡ { 0 , λ 1 + 1 2 } , C m } \lambda_{k+1}=\min\{\max\{0,\lambda_{1+\frac{1}{2}}\},\frac{C}{m}\} λk+1​=min{max{0,λ1+21​​},mC​}

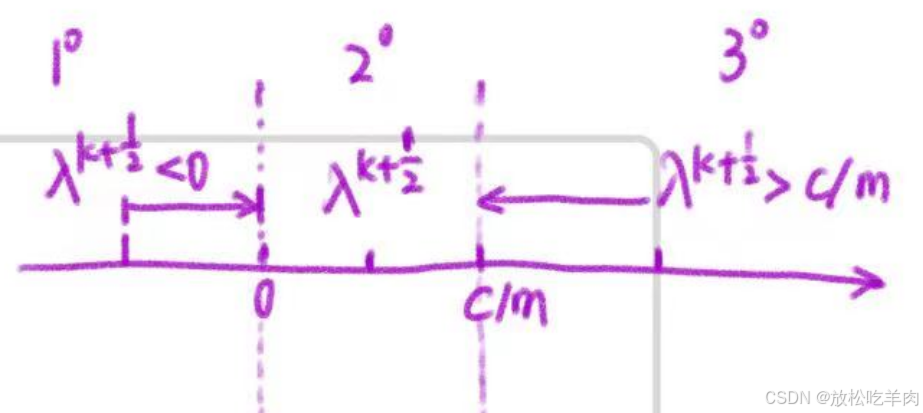
【说明】：在step 2.2中，${\lambda }_{k+1}=\arg \underset{\lambda }{\min }||\lambda -{\lambda }_{k+\frac{1}{2}}||$，画图可知，当 ${\lambda }_{k+\frac{1}{2}}<0$ 时，把它归到0，当 ${\lambda }_{k+\frac{1}{2}}>\frac{C}{m}$ 时，在 C/m 处截断，即 λ k + 1 = min ⁡ { max ⁡ { 0 , λ 1 + 1 2 } , C m } \lambda_{k+1}=\min\{\max\{0,\lambda_{1+\frac{1}{2}}\},\frac{C}{m}\} λk+1​=min{max{0,λ1+21​​},mC​}。