NLP学习路线第一章-----掌握相关机器学习方法内容

原创

已于 2024-01-08 22:56:46 修改 · 1.1k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#自然语言处理 #学习 #机器学习

于 2024-01-05 21:34:27 首次发布

本文探讨了机器学习中的线性回归与对数几率回归，重点介绍了XGBoost（集成学习算法）的原理、与GBDT的区别，以及HMM和CRF（条件随机场）在序列建模中的应用，包括概率计算、序列标注和参数估计等内容。

本文结合了博主的文章（机器学习分类算法之XGBoost（集成学习算法）--王小王-123）与自己的学习笔记，自己也没有学到位，因此仅供参考，也欢迎大家的指正。

一、线性回归与对数几率回归

线性回归（ $y=wx+b$ )的关键问题在于确定参数 w 和 b ，使得拟合输出和真实输出之间尽可能接近。在回归任务中，我们通常使用均方误差来度量预测与标签之间的损失，所以回归任务的优化目标就是使拟合输出与真实输出之间的均方误差最小化。

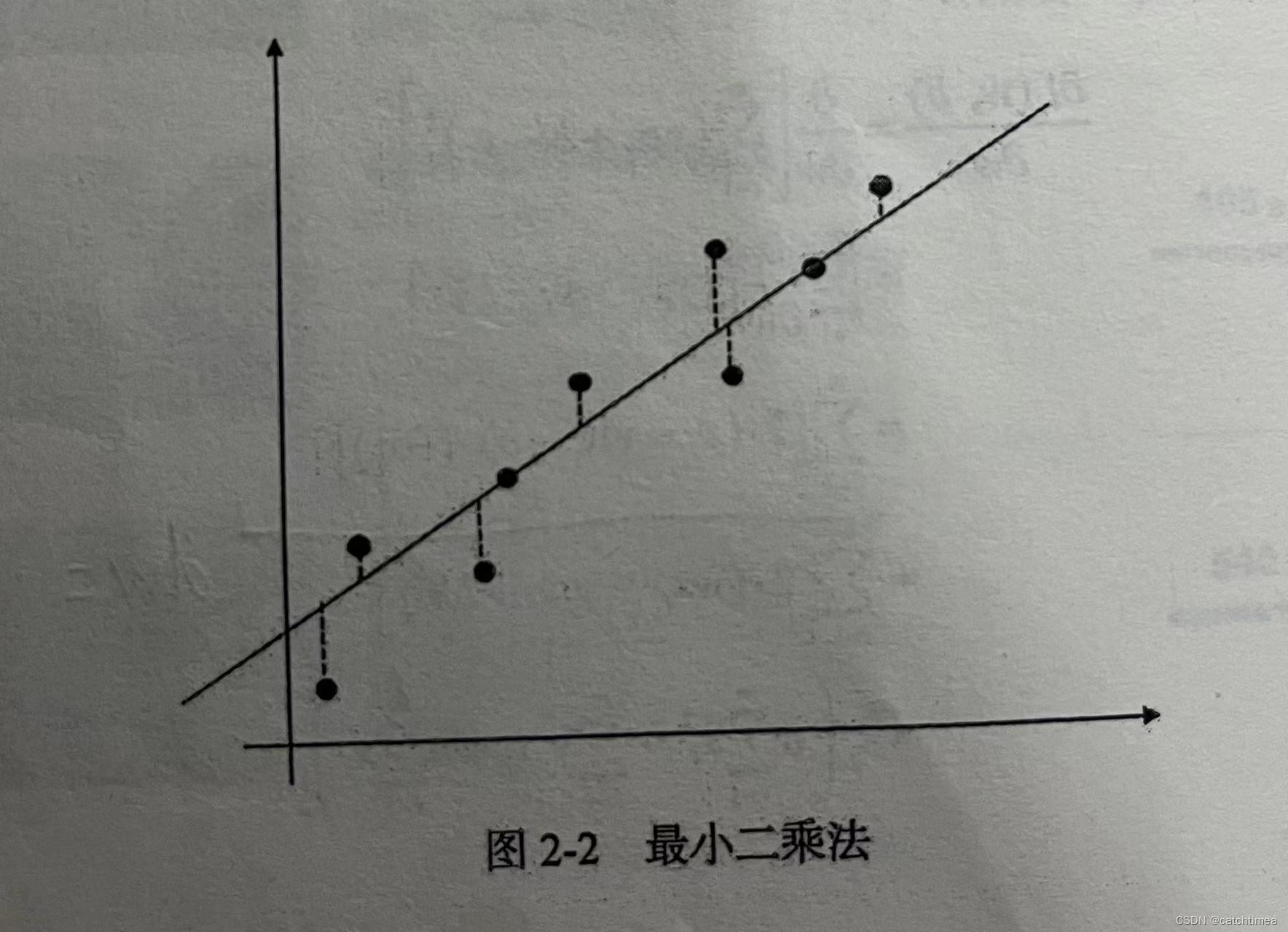
基于均方误差最小化的最小二乘法是线性回归模型求解的基本方法，通过最小均方误差和R平方系数可以评估线性回归的拟合效果。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。

基于 sklearn 的线性回归模型：

from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score

regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)

y_pred = regr.predict(X_test)

print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print("R Square score: %2.f" % r2_score(y_test, y_pred))

对数几率回归是一种线性分类模型。

线性模型如何执行分类任务呢？只需要找到一个单调可微函数将分类任务的真实标签y与线性回归模型的预测值进行映射。在线性回归中，我们直接令模型学习逼近真实标签y，但在对数几率回归中，我们需要找到一个映射函数将线性回归的预测值转化为0/1值。

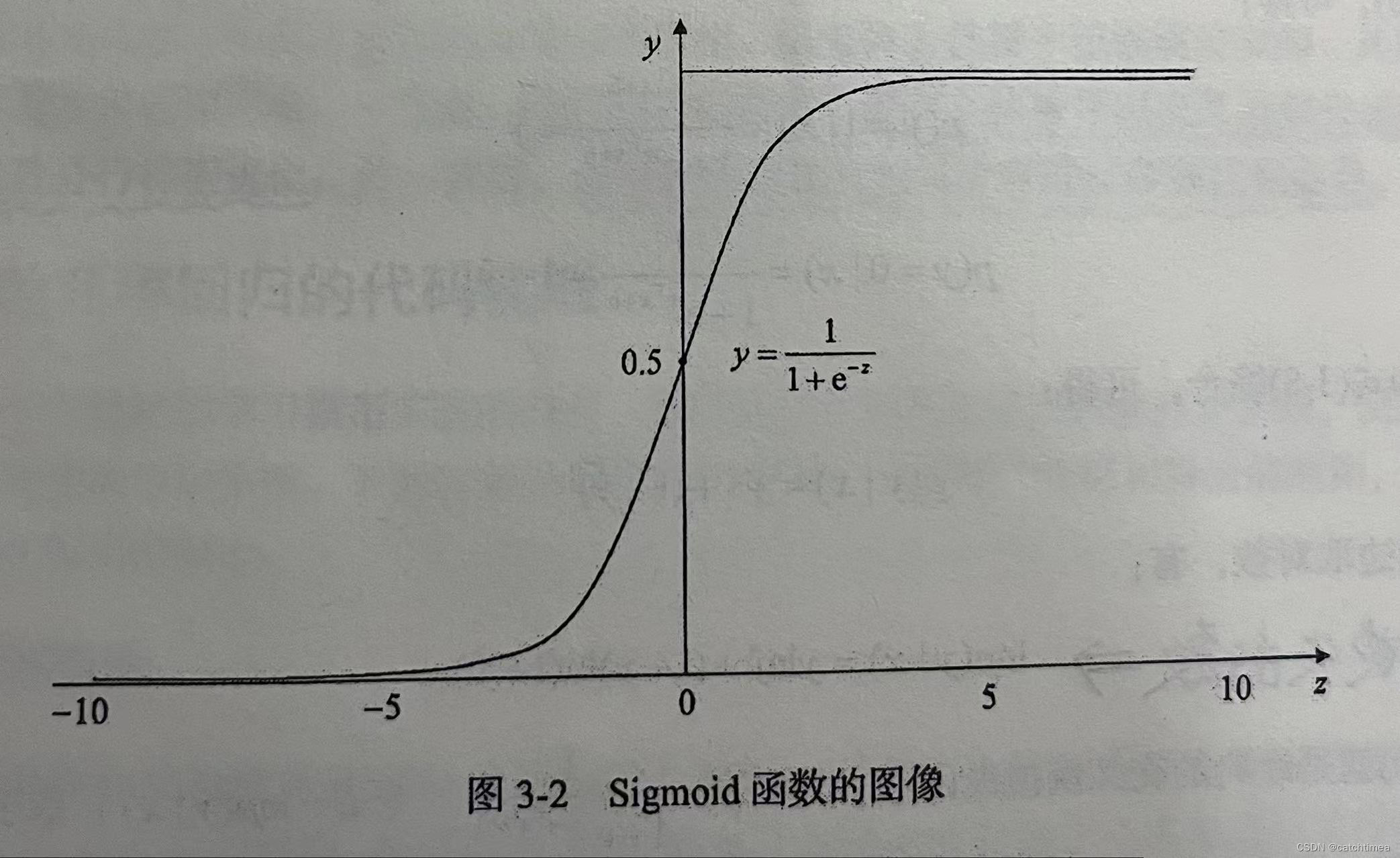
Sigmoid函数正好具备上述条件，单调可微，取值范围为（0，1），具有良好的求导特性且导数可用自身来表达。Sigmoid函数的图像如下图所示。

下面为对数几率回归的数学推导内容。

作为一种线性分类模型，对数几率回归在金融风控、计算广告、推荐系统和医疗健康领域都有着广泛应用。对数几率回归是用线性回归的结果来拟合真实标签的对数几率。同时，我们也可以将对数几率回归看作由条件概率分布表示的分类模型。另外，对数几率回归也是感知机模型、神经网络和支持向量机等模型的基础。

二、XGBoost

1. 什么是XGBoost？

名称	XGBoost (eXtreme Gradient Boosting )
作者	陈天奇（华盛顿大学博士）
基础	GBDT
所属	boosting迭代型、树类算法
适用范围	分类、回归
优点	速度快、效果好、可处理大规模数据、支持多种语言和自定义函数等。
缺点	算法参数过多，调参复杂、不适合处理