蓝桥杯，算法训练 礼物 C++ 详情解析(二分法和贪心)

问题描述

　　JiaoShou在爱琳大陆的旅行完毕，即将回家，为了纪念这次旅行，他决定带回一些礼物给好朋友。
　　在走出了怪物森林以后，JiaoShou看到了排成一排的N个石子。
　　这些石子很漂亮，JiaoShou决定以此为礼物。
　　但是这N个石子被施加了一种特殊的魔法。
　　如果要取走石子，必须按照以下的规则去取。
　　每次必须取连续的2*K个石子，并且满足前K个石子的重量和小于等于S，后K个石子的重量和小于等于S。
　　由于时间紧迫，Jiaoshou只能取一次。
　　现在JiaoShou找到了聪明的你，问他最多可以带走多少个石子。

输入格式

　　第一行两个整数N、S。
　　第二行N个整数，用空格隔开，表示每个石子的重量。

输出格式

　　第一行输出一个数表示JiaoShou最多能取走多少个石子。

样列输入

　　8 3
　　1 1 1 1 1 1 1 1

样列输出

　6

样列解释

　　任意选择连续的6个1即可。

数据规模和约定

　　对于20%的数据：N<=1000
　　对于70%的数据：N<=100,000
　　对于100%的数据：N<=1000,000，S<=10^12，每个石子的重量小于等于10^9，且非负

---

        这里我们介绍两种方法二分法和贪心(因数据过大超时) ，但是思路都会讲解一遍。

        方法一：二分法

        我们通过简单二分，拆出两部分来，一开始确定 l、r、mid的位置，l为起始位置，r为最后的石子，mid为中间位置 mid = (l + r)/2，且mid也表示K（1~mid）值，即一边所能拿的石子个数。确定左右两边拿的石子个数后，判断在位置mid的左右两边的石子个数是否有mid个，有则判断是否符合质量和小于等于S。代码解释已经很详细，看代码解析。不会含义的自己跟着代码动手画一画流程，便能理解到位。 

图解：

         

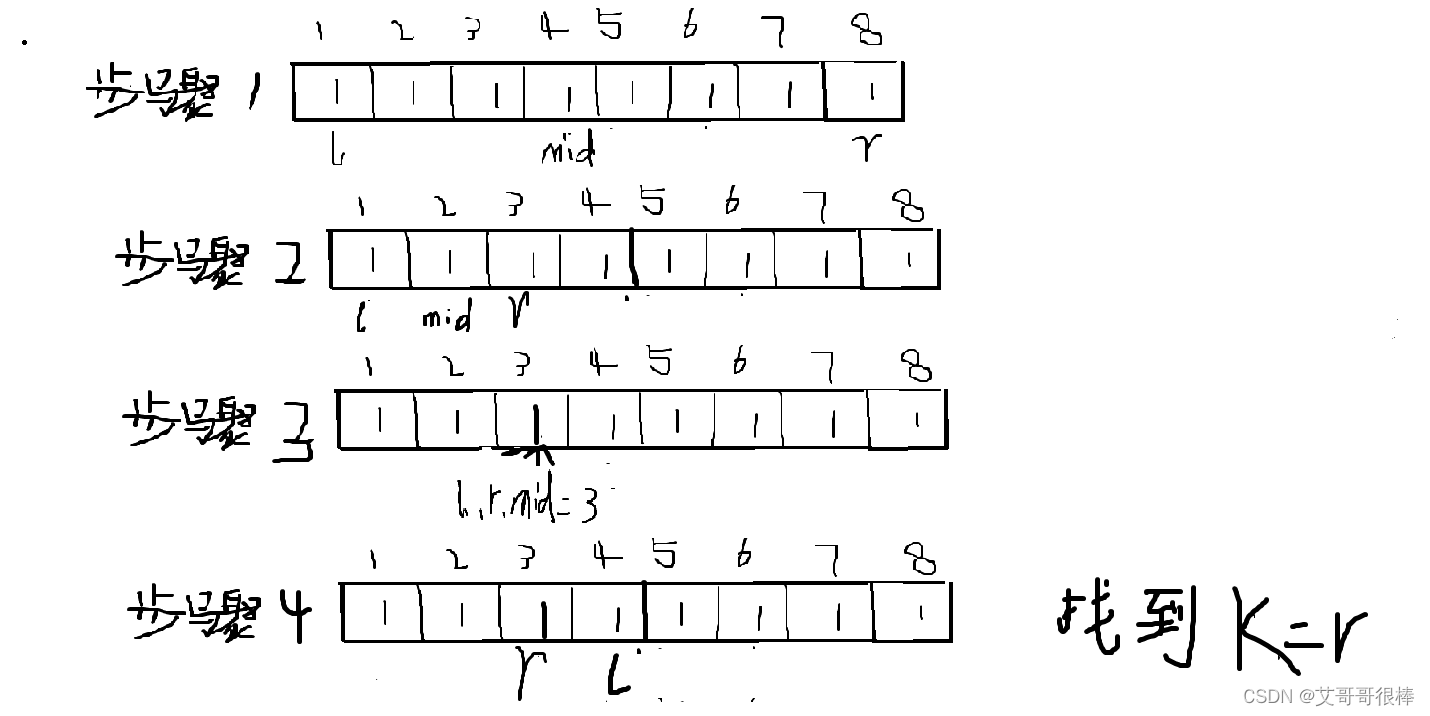
代码： 

#include<iostream>
using namespace std;

typedef long long ll;
const int N = 1e6 + 5;
ll val[N];     //记录重量之和
ll s;
int n;

//该函数的作用是，检查该长度下是否存在符合小于等于S的情况（mid代表其长度）
bool Check(int mid) {	
	for (int i = mid; i <= (n - mid); i++) {
		if ((val[i] - val[i - mid]) <= s && (val[i + mid] - val[i]) <= s) {
			return true;		//存在符合的长度
		}
	}
	return false;
	
}

int main() {
	int l, r, mid;
	ios::sync_with_stdio(false);	//取消输入输出缓存，加快cin、cout运算时间
	cin >> n >> s;
	for (int i = 1; i <= n; i++) {
		cin >> val[i];
		val[i] += val[i - 1];		//滚动遍历1到i个石子的重量和
	}

	l = 1; r = n;
	while (l <= r) {
		mid = (l + r) / 2;
		if (Check(mid)) {
			l = mid + 1;		//该长度下存在符合的连续数，返回l后，
		}						//mid长度加一，继续寻找更大长度下是否存在
		else {
			r = mid - 1;		//该长度下不存在符合的连续数，返回r后，
		}						//mid长度减一，继续寻找更小长度下是否存在

	}

	cout << 2 * r << endl;		//r所在的位置就是一边的最大长度
	return 0;
}

方法二：贪心(数据过大超时，仅作为参考理解方法)

        贪心就是从1到N，让每个数当作中心点，然后求出左右两边的数能符合条件的的情况。最后显出最大K，输出2*K；

代码：

#include<iostream>
using namespace std;

typedef long long ll;
#define N int(1e6 + 5)

ll val[N] = { 0 };			//记录前面的数之和
ll s;

int main() {
	int n, ans = 0;
	int a, b;			//记录k的左右两边最多有几个数符合
	ios::sync_with_stdio(false);	//关闭流同步,加快cin，cout速度
	cin >> n >> s;

	for (int i = 1; i <= n; i++) {
		cin >> val[i];
		val[i] += val[i - 1];			//记录1到i个石子的重量和
	}

	for (int k = 1; k < n; k++) {
		a = 0;
		b = 0;

		if (ans >= (n - k)) break;		//若后面剩余的数小于等于ans，则找不出比ans更大连续数

		for (int i = k - 1; i >= 0; i--) {		//前半部分从k+1个数开始，找符合条件的

			if ((val[k] - val[i]) > s) {
				a = k - i - 1;			//记录此时符合前K个数之和小于S的K
				break;
			}
			else if (i == 0) {
				a = k;					//前K个数都符合，之和小于等于S
			}
		}

		for (int i = k + 1; i <= n; i++) {		//后半部分从k+1个数开始，找符合条件的
			if ((val[i] - val[k]) > s) {
				b = i - k - 1;
				break;
			}
			else if (i == n) {
				b = i - k;
			}
		}
		ans = max(ans, min(a, b));
	}

	cout << 2 * ans << endl;
	return 0;
}