3.7 最大异或对

异或

二进制位同为0，异为1
异或符号 ^
异或性质：
a^a=0 a^0=0
(a^ b ^c) =(a^c ^b)

一道异或的题目

最大异或对

题目链接

思路

注重思维方式

1. 首先是暴力想法，使用两重循环，对每两个数字进行取异或运算，得出最大值
2. 考虑如何优化。
3. 首先，两重for循环的第一层无法优化，因为确实需要至少枚举一次数字。那么考虑优化第二层。
4. 那么这么想，如果给定了一个固定的数字a，我们如何找到另外一个数字b使得 a^b最大。因为异或运算，从二进制角度思考，如果我们想让一个数最大，那么这个数的高位应该是1
   
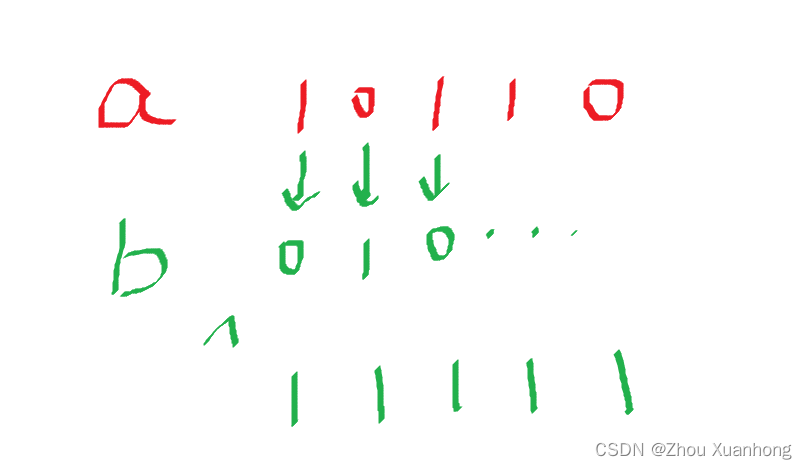
   如上图，对于a=10110，我们要找的b就最好每一位都是a的每一位取!,这样异或出来就是11111，这样就是最大的
5. 那么第二重循环的目的就是，如何快速找到这样的b。因此我们考虑使用Trie树存储某个数的二进制表示：
   
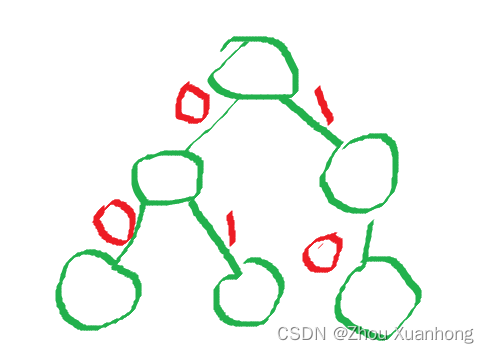
   如果我们像这样存储数字，那么在查找时就可以从树根往下找我们想要的!的数字。另一支就根本不用考虑。注意，树从上往下应该是从高位到地位，符合贪心的思维，因此可以得到最大值。
6. 由此可见，思路就很明显了：用Trie树存储所有的数字（二进制从高位到低位存储），然后两层循环，第一层用于遍历所有数值，固定住此时的a。第二层用于搜寻对于a，Trie树中哪一个b使得a^b更大。最后比较每一个a所对应的a ^ b即可。

关于二进制数位的运算在代码中详细解释。详见代码注释。

实现代码

#include<iostream>
#include<algorithm>

using namespace std;

//N用于标注数字的数量，M用于标注节点的数量。
//由于每个数字的范围是0-2^31，因此位数最多31位，最多1e5个数字，节点总数最多为31*1e5约为3*1e6 
const int N=1e5+10,M=3*1e6+1e5;

//定义Trie树，不需要用记录num的数组，因为如果不存在，后面都是0，对于异或运算没影响 
int son[M][2],idx=0;
int a[N];//用于存放数字的数组 

void insert(int x){
	//将x插入Trie树
	
	int p=0;
	for(int i=30;i>=0;i--){
		//这里是30是因为数字范围是0-2^31,int第一位是符号位，这里用不到，后面一共31位，因此从30到0，自己体会 
		int u=(x>>i&1);//提取出x的某一位二进制 
		if(son[p][u]==0)//如果当前位没存
			son[p][u]=++idx; 
		p=son[p][u]; 
	} 
	
}

int search(int x){
	//搜寻能使得和当前x异或最大的数字 
	
	int p=0,res=0;//res是最大的结果值 
	for(int i=30;i>=0;i--){
		int u=(x>>i&1);
		//获得当前x二进制位的数字（从高到低）
		if(son[p][!u]){//如果和该位置 ! （非）存在，注意这里是!
			//那么就按照这条路走，并更新值
			res+=(1<<i); //左移运算嘛，还记得嘛。 
			p=son[p][!u]; 
		}
		else{//如果该位置没有可以!的 
			//那么不用res+=，因为该位结果是0，不需要加
			p=son[p][u];//没办法，只能按照u走，不能按照!u走 
		}
	}
	return res;
} 



int main(){
	
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		insert(a[i]);
	}		
	
	int ans=0;
	
	for(int i=1;i<=n;i++){
		ans=max(ans,search(a[i]));
	}
	
	cout<<ans<<endl;
		
	return 0;
} 

注意
犯了一个很笨比的错误
将！用成了~
!是反转其操作数，用于将0->1, 1->0, 隐式地将true和false转化
而~是按位取反 对于 ~0 ，按位取反后是11111… 值是-1（符号位）
太笨比了，确实数值转化没仔细学过