校课程的简单实验报告。
北京大学出版社-算法设计与分析
一、实验目的
1.掌握回溯法的基本思想;
2.掌握回溯法的算法框架;
3.掌握回溯法的基本应用。
二、实验内容
使用回溯法求解以下问题,要求给出程序代码,并编译运行程序:
1.P149习题3。
2.P150习题4。
三、实验环境
1. 使用的操作系统及版本:
Windows 10
2. 使用的编译系统及版本:
CLion 2022.2.3
四、实验步骤及说明
1、P149习题3
n对括号组成的合法表达式(即n个左括号和n个右括号组成的合法括号序列)
实质为卡特兰数
n对括号、n个结点的二叉树个数、出栈序列个数
即LeetCode22.
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
代码如下:
//
// Created by GiperHsiue on 2022/11/28.
//
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
// 括号
class Solution {
vector<string> res;
int sum;
bool *sta;
public:
// O() O() 回溯 子集树
vector<string> generateParenthesis(int n) {
if(!n) return {""};
sum = n * 2;
sta = new bool[sum];
memset(sta, 1, sum);
// for(int i = 0; i < sum; i ++) sta[i] = true;
sta[0] = false;
dfs(1, 0, 1);
return res;
}
void dfs(int lcnt, int rcnt, int pos){
if(lcnt + rcnt == sum){
string tmp = check();
res.emplace_back(tmp);
return;
}
for(int j = 0; j < 2; j ++){
if(!j){
if(lcnt < sum / 2){
sta[pos] = 0;
dfs(lcnt + 1, rcnt, pos + 1);
}
}
else{
if(rcnt < lcnt){
sta[pos] = 1;
dfs(lcnt, rcnt + 1, pos + 1);
}
}
}
}
string check(){
string tmp;
for(int i = 0; i < sum; i ++){
if(!sta[i]) tmp += "(";
else tmp += ")";
}
return tmp;
}
};
int main(){
int n;
cin >> n;
Solution so;
vector<string> res;
res = so.generateParenthesis(n);
for(auto &x:res) cout << x << ' ';
}
测试如下:
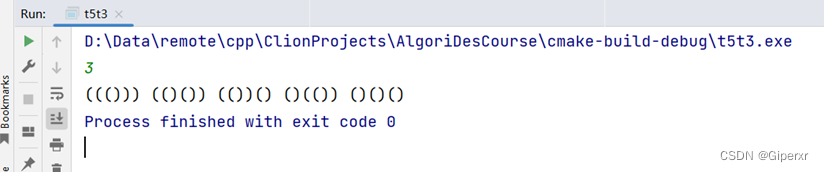
P150习题4
给定一个仅包含数字2 ~ 9 的字符串, 返回所有可能它能表示的字母组合.

即LeetCode17.
代码如下:
//
// Created by GiperHsiue on 2022/12/1.
//
// P150T4 给定一个仅包含数字2 ~ 9 的字符串, 返回所有可能它能表示的字母组合。
#include <iostream>
#include <string>
#include <unordered_map>
#include <vector>
using namespace std;
void dfs(vector<string>& strtmp, vector<string>& res, string tmp, int deep);
// strtmp存储给定字符串digits所对应的映射字母 res存储字母组合答案
// tmp临时track deep判断到第几个(0 ~ n - 1)
void dfs(vector<string>& strtmp, vector<string>& res, string tmp, int deep) {
if (deep == strtmp.size()) {
res.emplace_back(tmp);
return;
}
for (int i = 0; i < strtmp[deep].size(); i++) {
tmp[deep] = strtmp[deep][i];
// cout << tmp << endl;
dfs(strtmp, res, tmp, deep + 1);
}
}
vector<string> letterCombinations(string digits) {
vector<string> res; // 存储答案
if (digits.size() == 0) {
return res;
}
unordered_map<char, string> tmap; // hash映射
// 建立映射关系
char tmchar = 'a';
for (char i = '2'; i < '7'; i++) {
string tmpstr = " ";
tmpstr[0] = tmchar++, tmpstr[1] = tmchar++, tmpstr[2] = tmchar++;
// cout << tmpstr << endl;
tmap[i] = tmpstr;
}
tmap['7'] = "pqrs";
tmap['8'] = "tuv";
tmap['9'] = "wxyz";
// for(auto&[k, v]:tmap) cout << k << ' ' << v << ' ';
// 存储给定字符串digits所对应的映射字母
int n = digits.size();
vector<string> strtmp;
for (int i = 0; i < n; i++) {
strtmp.emplace_back(tmap[digits[i]]);
}
// cout << strtmp.size() << endl;
// for(auto &x:strtmp) cout << x << ' ' << endl;
string varSavtmp(n, ' ');
dfs(strtmp, res, varSavtmp, 0);
return res;
}
int main() {
string digits;
cin >> digits;
vector<string> res;
res = letterCombinations(digits);
// cout << res.size() << endl;
for (auto& x : res)
cout << x << ' ';
return 0;
}
测试如下:
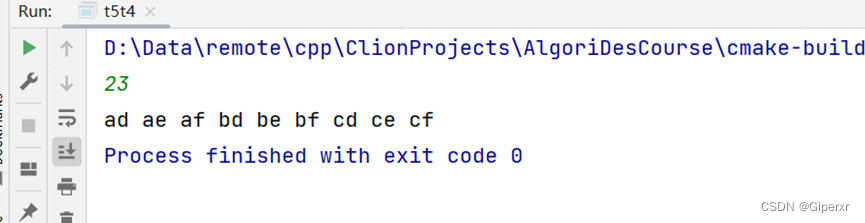
五、实验小结及思考
通过本次实验,让我对于回溯算法有了进一步的了解与认识。回溯法通过dfs深度优先搜索去遍历树,分为子集树和排列树,像上面第三题就是使用子集树,第四题是排列树的变形也就是组合。








 本文是一份关于算法设计与分析的实验报告,重点介绍了回溯法的应用,包括P149和P150两个习题的解决方案,涉及括号组合和数字转字母组合的问题。通过实验,学生深化了对回溯法的理解和实践能力。
本文是一份关于算法设计与分析的实验报告,重点介绍了回溯法的应用,包括P149和P150两个习题的解决方案,涉及括号组合和数字转字母组合的问题。通过实验,学生深化了对回溯法的理解和实践能力。

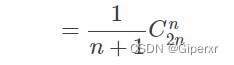


















 1419
1419

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








