A Runtime- and Cost-Efficient Approach of Deploying Mixture-of-Experts in Edge Networks
这篇文章通过提出一种名为 NFC-MoED (Neighbor-First Centrality-based Mixture of Expert layer Deployment) 的算法来实现部署成本的减少。其核心思想是通过一个启发式的度量指标 NFC (Neighbor-First Centrality) 来快速评估和决定混合专家模型(MoE)中各个组件(尤其是Router & Aggregator, R&A)的部署位置,并在此基础上部署专家模型(EMs)。
一、专家模型成本优化的实现方法
1. 问题定义 (MoED)
-
目标:最小化部署 MoE 层的总成本,包括计算成本、存储成本和带宽成本。
-
R&A (Router & Aggregator) 统一处理: 将 MoE 层中的路由器 (Router) 和聚合器 (Aggregator) 视为一个统一的部署组件 (R&A),因为他们在功能上的紧密耦合和数据流的连续性
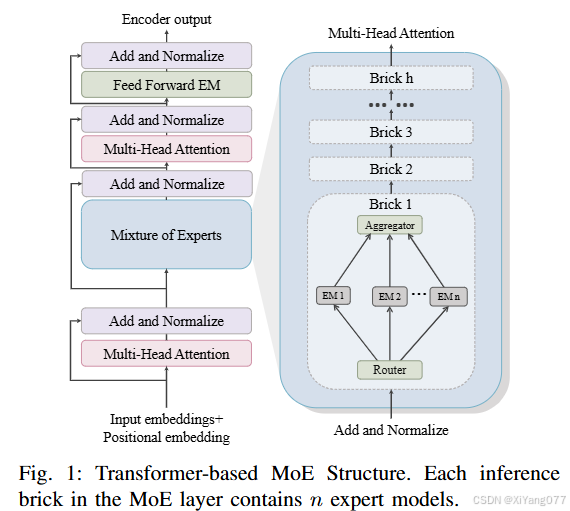
对于为什么“R&A (Router & Aggregator)可以统一处理”的一些补充说明
- 功能上的紧密耦合(Tightly Coupled Functionality):
- 路由器的作用:接收输入,并根据输入特征决定将数据路由到哪些专家模型(EMs)进行处理。
聚合器的作用:收集被激活的专家模型(EMs)的输出,并将这些输出组合(例如,加权求和)起来,形成MoE层的最终输出。 - 路由器和聚合器共同构成了专家选择和结果汇总的核心机制。路由器的选择直接决定了哪些专家的输出会被聚合器使用。它们的功能是相互依赖、密不可分的。论文中提到:“Given their joint role in directing internal data flow, the router and aggregator are tightly coupled and can be treated as a unified deployment component, denoted as R&A.” (鉴于它们在指导内部数据流方面的联合作用,路由器和聚合器是紧密耦合的,可以被视为一个统一的部署组件,表示为R&A。)
- 路由器的作用:接收输入,并根据输入特征决定将数据路由到哪些专家模型(EMs)进行处理。
- 数据流的连续性(Sequential Data Flow): 数据首先进入路由器,路由器将数据分发给选定的EMs。EMs处理数据后,其输出被发送到聚合器。聚合器整合这些输出。 从逻辑上看,路由器是EMs处理阶段的“入口”,聚合器是EMs处理阶段的“出口”。将它们部署在一起可以简化对这一核心处理单元的管理和通信。
- 许多MoE框架(如论文中提到的DBRX的REA结构:Router-Expert models-Aggregator)在逻辑上就是将这三者视为一个紧密协作的单元。将R和A捆绑部署,更贴近这种逻辑结构。
- 功能上的紧密耦合(Tightly Coupled Functionality):
-
NFC (Neighbor-First Centrality) 度量: 为了快速确定 R&A 的位置,并避免传统最短路径算法带来的高时间复杂度,文章提出了一种新的度量标准——邻居优先中心性 (NFC)。NFC 度量 (Eq.21) 为每个潜在的 R&A 部署节点 n n n 计算一个中心性得分。这个得分综合考虑了在该节点部署 R&A 的成本,以及将 EMs 部署在其邻近节点上的预期平均成本 g ( m , n ) g(m,n) g(m,n) (Eq. 20)。
2. NFC-MoED 算法
(1)算法思路
- 核心假设: 当 R&A 部署在某个节点 n n n 时,专家模型 (EMs) 最好被放置在其邻近的节点上。
- R&A 位置选择:算法遍历所有物理节点,将每个节点作为 R&A 的候选部署位置。
- EM 优先部署在邻居节点:对于每个候选 R&A 节点 n n n,算法优先将 EMs 部署在 g ( m , n ) g(m,n) g(m,n) 值最低的邻居节点上(即预期部署成本最低的邻居),直到所有 EMs 都被部署。
- 选择最优R&A位置:计算每个候选 R&A 节点 n n n 的 NFC 值,并选择具有最低 NFC 值的节点作为最终的 R&A 部署位置。与之对应的EM部署方案也随之确定。
NFC-MoED 通过 NFC 这个启发式度量,牺牲了寻找绝对全局最优解的保证,换来了 极高的运行时效率 和 近乎最优的部署成本。
(2)NFC 计算
NFC 计算 (Eq. 21): N F C n = Σ m ∈ N ′ ( g ( m , n ) ∗ n u m n s ) + C R ∗ P n C + C A ∗ P n C NFCn = Σ_{m∈N'} (g(m, n) * num_n^s) + CR * P_n^C + CA * P_n^C NFCn=Σm∈N′(g(m,n)∗numns)+CR∗PnC+CA∗PnC
-
g
(
m
,
n
)
g(m,n)
g(m,n) (Eq. 20): 在节点
n
n
n 托管 R&A 的情况下,将一个 EM 部署到节点
m
m
m 的预期平均成本。它由计算成本
g
c
(
m
,
n
)
gc(m,n)
gc(m,n),存储成本
g
s
(
m
,
n
)
gs(m,n)
gs(m,n)和带宽成本
g
b
w
(
m
,
n
)
gbw(m,n)
gbw(m,n)组成,
g
(
m
,
n
)
=
(
g
c
(
m
,
n
)
+
g
s
(
m
,
n
)
+
g
b
w
(
m
,
n
)
)
/
n
u
m
m
s
g(m,n) = (gc(m,n) + gs(m,n) + gbw(m,n)) /num_m^s
g(m,n)=(gc(m,n)+gs(m,n)+gbw(m,n))/numms
-
n
u
m
m
s
=
⌊
(
S
m
−
S
M
O
E
)
/
S
v
⌋
num_m^s = \lfloor (S_m - S_{MOE}) / S_v \rfloor
numms=⌊(Sm−SMOE)/Sv⌋表示在物理节点
m
m
m上能够托管的最大专家模型数量
S m S_m Sm:物理节点 m m m的总可用存储容量(Total storage capacity of node m m m)
S M O E S_{MOE} SMOE:共享预训练基础模型 (FPM) 所需的存储空间 (Storage requirement for the shared pre-trained foundation model),这个是所有专家模型在节点 m m m上共用的,只需要存储一份。
S v S_v Sv:单个专家模型 (EM) 所需的存储空间n u m m s num_m^s numms公式的推导逻辑:
- 预留共享模型的存储:
在一个部署了MoE模型的节点 m m m 上,首先必须为共享的预训练基础模型 (FPM) 预留存储空间。因为无论这个节点上部署多少个专家模型(只要至少有一个),这个共享模型都必须存在。所以,节点 m m m 用于存储专家模型本身的可用存储空间是 S m − S M O E S_m - S_{MOE} Sm−SMOE。
2. 计算可容纳的专家数量:
在扣除了共享模型的存储后,剩余的存储空间 ( S m − S M O E ) (S_m - S_{MOE}) (Sm−SMOE) 就可以全部用来存储各个独立的专家模型了。
由于每个专家模型需要 S v S_v Sv 的存储空间,那么用剩余的总可用存储空间除以单个专家所需的存储空间,就可以得到理论上可以容纳的专家模型数量:
( S m − S M O E ) / S v (S_m - S_{MOE}) / S_v (Sm−SMOE)/Sv
3. 取整处理 (论文中的向下取整 ⌊ ⋅ ⌋ \lfloor \cdot \rfloor ⌊⋅⌋):
因为专家模型的数量必须是整数(你不能部署0.5个专家模型),所以需要对上述计算结果进行取整。通常情况下,我们能部署的专家数量不能超过计算出的理论值,所以应该向下取整 (floor function)。
- 预留共享模型的存储:
-
g c ( m , n ) = n u m m α ∗ C v ∗ P m c gc(m,n) = num_m^α * C_v * P_m^c gc(m,n)=nummα∗Cv∗Pmc 代表将专家模型(EMs)部署在节点 m m m上,而R&A部署在节点 n n n 上的预期计算成本。
P m c P_m^c Pmc代表计算的单位成本。
n u m m a = m i n ( n u m m s , α n u m ) num_m^a = min(num_m^s, α_{num}) numma=min(numms,αnum)表示在节点 m m m 上实际激活的专家模型数量n u m m a num_m^a numma公式的推导逻辑:
一个节点 m m m 上实际能够参与工作(被激活)的专家模型数量,取决于两个因素的较小者:① 该节点 m m m物理上最多能部署多少个专家模型 ( n u m m n num_m^n nummn)。② 系统在一次推理中允许激活多少个专家模型 ( α n u m α_{num} αnum)。
即使一个节点有能力部署很多专家,但如果系统每次推理只激活少数几个,那么实际在该节点上被激活的专家数量也不会超过系统设定的激活上限。反之,如果系统允许激活很多专家,但节点物理容量有限,那么实际激活的专家数量也不会超过该节点的物理容纳能力。 -
g s ( m , n ) = n u m m s ∗ S v ∗ P m s + S M O E ∗ P m s gs(m,n) = num_m^s * S_v * P_m^s+ S_{MOE} * P_m^s gs(m,n)=numms∗Sv∗Pms+SMOE∗Pms代表将专家模型(EMs)部署在节点 m m m上,而R&A部署在节点 n n n 上的总存储成本。
P m s P_m^s Pms代表存储的单位成本。 -
g b w ( m , n ) = h o p m , n ∗ P l m , n ∗ ( B W R + B W A ∗ n u m m s ) gbw(m,n) = hop_{m,n} * P_{lm,n} * (BW_R + BW_A * num_m^s) gbw(m,n)=hopm,n∗Plm,n∗(BWR+BWA∗numms)代表将专家模型(EMs)部署在节点 m m m上,而R&A部署在节点 n n n 上的预期带宽成本。
h o p m , n hop_{m,n} hopm,n代表从节点 m m m到节点 n n n 之间的网络跳数。这是对网络距离的一种简化度量,用以近似实际的路径长度或延迟。NFC 度量使用跳数来避免复杂的最短路径计算,从而提高评估效率。
P l m , n P_{lm,n} Plm,n代表物理链路上每单位带宽的单位成本
B W R BW_R BWR代表从Router到EMs 的带宽需求。
B W A BW_A BWA代表从 从每个EM到Aggregator的带宽需求
-
n
u
m
m
s
=
⌊
(
S
m
−
S
M
O
E
)
/
S
v
⌋
num_m^s = \lfloor (S_m - S_{MOE}) / S_v \rfloor
numms=⌊(Sm−SMOE)/Sv⌋表示在物理节点
m
m
m上能够托管的最大专家模型数量
关于 n u m m s num_m^s numms和 n u m m a num_m^a numma的说明
公式 (15) 中的是 n u m m a num_m^a numma(实际激活数量),因为计算与激活相关。
公式 (16) 中的是 n u m m s num_m^s numms(物理部署数量),因为存储与部署相关。
公式 (17) 中的是 n u m m a num_m^a numma(实际激活数量),因为带宽与实际通信的激活专家相关。
为什么论文在计算初始的 g ( m , n ) g(m,n) g(m,n) 以进行节点排序时,直接使用了节点能托管的最大专家数量 n u m m s num_m^s numms(在图3的推演中,它被当作 n u m m a num_m^a numma使用了)?
在算法的早期阶段(即决定R&A部署位置,并对潜在的EM托管节点进行排序时),我们并不知道未来具体的推理请求会激活哪些EM,以及激活多少个。因此为了得到一个通用的、衡量节点“性价比”的指标 g ( m , n ) g(m,n) g(m,n),论文选择了一种最坏情况或平均情况的近似。使用节点能承载的最大数量 n u m m s num_m^s numms (这里用 n u m m a num_m^a numma 表示这个最大承载量) 可以看作是评估该节点在满负荷或接近满负荷运行EM时的平均单位成本。
- C R ∗ P C n + C A ∗ P C n CR * P_C^n + CA * P_C^n CR∗PCn+CA∗PCn: R&A 自身的计算成本
二、文章中模拟过程 (Fig. 2 & Fig. 3) 的详细推导过程
问题假设:
-
物理网络和 MoE 结构如 Fig. 2 所示。MoE 有 4 个 EMs,以及一个 Router 和一个 Aggregator (统一为 R&A)。
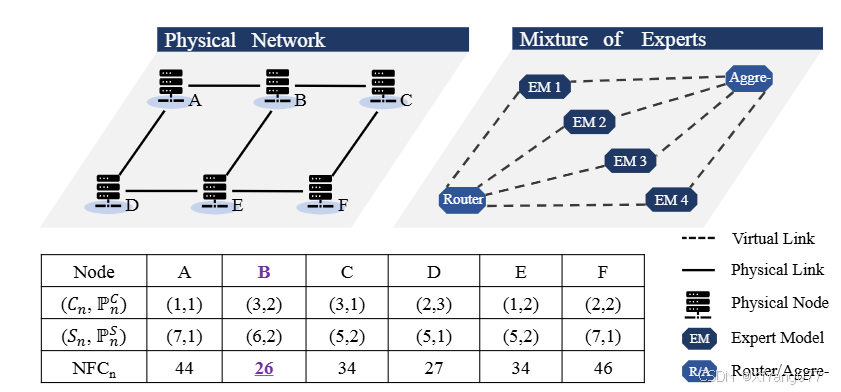
-
每个EM 需要 1 单位计算和 1 单位存储。( C v = 1 , S v = 1 C_v=1,S_v=1 Cv=1,Sv=1)
-
共享预训练基础模型 (FPM) 需要 4 单位存储 ( S M O E = 4 S_{MOE}=4 SMOE=4 )。
-
链路有足够带宽 (用于简化 NFC 计算中的带宽成本估算,主要看跳数)。
问题详细推导过程
假设 R&A 部署在节点 B(n=B)
N
F
C
B
=
Σ
m
∈
N
′
(
g
(
m
,
B
)
∗
n
u
m
B
s
)
+
C
R
∗
P
B
C
+
C
A
∗
P
B
C
NFCB = Σ_{m∈N'} (g(m, B) * num_B^s) + CR * P_B^C + CA * P_B^C
NFCB=Σm∈N′(g(m,B)∗numBs)+CR∗PBC+CA∗PBC
g
(
m
,
B
)
=
(
g
c
(
m
,
B
)
+
g
s
(
m
,
B
)
+
g
b
w
(
m
,
B
)
)
/
n
u
m
m
s
g(m,B) = (gc(m,B) + gs(m,B) + gbw(m,B)) /num_m^s
g(m,B)=(gc(m,B)+gs(m,B)+gbw(m,B))/numms
Step1:部署 4 个 EMs 到 B 的邻居 (Neighbor-First)
B的邻居是A,C,E
-
对于A,m=A, n=B
n u m A s = ⌊ ( S A − S M O E ) / S v ⌋ = ⌊ ( 7 − 4 ) / 1 ⌋ = 3 num_A^s = \lfloor (S_A - S_{MOE}) / S_v \rfloor=\lfloor(7-4)/1\rfloor=3 numAs=⌊(SA−SMOE)/Sv⌋=⌊(7−4)/1⌋=3
g c ( A , B ) = n u m A α ∗ C v ∗ P A c = 3 ∗ 1 ∗ 1 = 3 gc(A,B) = num_A^α * C_v * P_A^c=3*1*1=3 gc(A,B)=numAα∗Cv∗PAc=3∗1∗1=3
g s ( A , B ) = n u m A s ∗ S v ∗ P A s + S M O E ∗ P A s = 3 ∗ 1 ∗ 1 + 4 ∗ 1 = 7 gs(A,B) = num_A^s * S_v * P_A^s+ S_{MOE} * P_A^s=3*1*1+4*1=7 gs(A,B)=numAs∗Sv∗PAs+SMOE∗PAs=3∗1∗1+4∗1=7
g b w ( A , B ) = h o p A , B ∗ P l A , B ∗ ( B W R + B W A ∗ n u m A s ) = 1 ∗ 1 ∗ ( 1.5 + 0.5 ∗ 3 ) = 3 gbw(A,B) = hop_{A,B} * P_{lA,B} * (BW_R + BW_A * num_A^s)=1*1*(1.5 + 0.5 * 3)=3 gbw(A,B)=hopA,B∗PlA,B∗(BWR+BWA∗numAs)=1∗1∗(1.5+0.5∗3)=3
g ( A , B ) = ( g c ( A , B ) + g s ( A , B ) + g b w ( A , B ) ) / n u m A s = ( 3 + 7 + 3 ) / 3 = 13 / 3 g(A,B) = (gc(A,B) + gs(A,B) + gbw(A,B)) /num_A^s=(3+7+3)/3=13/3 g(A,B)=(gc(A,B)+gs(A,B)+gbw(A,B))/numAs=(3+7+3)/3=13/3 -
对于C,m=C, n=B
n u m C s = ⌊ ( S C − S M O E ) / S v ⌋ = ⌊ ( 5 − 4 ) / 1 ⌋ = 1 num_C^s = \lfloor (S_C - S_{MOE}) / S_v \rfloor=\lfloor(5-4)/1\rfloor=1 numCs=⌊(SC−SMOE)/Sv⌋=⌊(5−4)/1⌋=1
g c ( C , B ) = n u m C α ∗ C v ∗ P C c = 1 ∗ 1 ∗ 1 = 1 gc(C,B) = num_C^α * C_v * P_C^c=1*1*1=1 gc(C,B)=numCα∗Cv∗PCc=1∗1∗1=1
g s ( C , B ) = n u m C s ∗ S v ∗ P C s + S M O E ∗ P C s = 1 ∗ 1 ∗ 2 + 4 ∗ 2 = 10 gs(C,B) = num_C^s * S_v * P_C^s+ S_{MOE} * P_C^s=1*1*2+4*2=10 gs(C,B)=numCs∗Sv∗PCs+SMOE∗PCs=1∗1∗2+4∗2=10
g b w ( C , B ) = h o p A , C ∗ P l A , C ∗ ( B W R + B W A ∗ n u m C s ) = 1 ∗ 1 ∗ ( 1.5 + 0.5 ) = 2 gbw(C,B) = hop_{A,C} * P_{lA,C} * (BW_R + BW_A * num_C^s)=1*1*(1.5 + 0.5)=2 gbw(C,B)=hopA,C∗PlA,C∗(BWR+BWA∗numCs)=1∗1∗(1.5+0.5)=2
g ( C , B ) = ( g c ( C , B ) + g s ( C , B ) + g b w ( C , B ) ) / n u m C s = ( 1 + 10 + 2 ) / 1 = 13 g(C,B) = (gc(C,B) + gs(C,B) + gbw(C,B)) /num_C^s=(1+10+2)/1=13 g(C,B)=(gc(C,B)+gs(C,B)+gbw(C,B))/numCs=(1+10+2)/1=13 -
对于E,m=A, n=B
n u m E s = ⌊ ( S E − S M O E ) / S v ⌋ = ⌊ ( 5 − 4 ) / 1 ⌋ = 1 num_E^s = \lfloor (S_E - S_{MOE}) / S_v \rfloor=\lfloor(5-4)/1\rfloor=1 numEs=⌊(SE−SMOE)/Sv⌋=⌊(5−4)/1⌋=1
g c ( E , B ) = n u m E α ∗ C v ∗ P E c = 1 ∗ 1 ∗ 2 = 2 gc(E,B) = num_E^α * C_v * P_E^c=1*1*2=2 gc(E,B)=numEα∗Cv∗PEc=1∗1∗2=2
g s ( E , B ) = n u m E s ∗ S v ∗ P E s + S M O E ∗ P E s = 1 ∗ 1 ∗ 2 + 4 ∗ 2 = 10 gs(E,B) = num_E^s * S_v * P_E^s+ S_{MOE} * P_E^s=1*1*2+4*2=10 gs(E,B)=numEs∗Sv∗PEs+SMOE∗PEs=1∗1∗2+4∗2=10
g b w ( E , B ) = h o p E , B ∗ P l E , B ∗ ( B W R + B W A ∗ n u m E s ) = 1 ∗ 1 ∗ ( 1.5 + 0.5 ) = 2 gbw(E,B) = hop_{E,B} * P_{lE,B} * (BW_R + BW_A * num_E^s)=1*1*(1.5 + 0.5)=2 gbw(E,B)=hopE,B∗PlE,B∗(BWR+BWA∗numEs)=1∗1∗(1.5+0.5)=2
g ( E , B ) = ( g c ( E , B ) + g s ( E , B ) + g b w ( E , B ) ) / n u m E s = ( 2 + 10 + 2 ) / 1 = 14 g(E,B) = (gc(E,B) + gs(E,B) + gbw(E,B)) /num_E^s=(2+10+2)/1=14 g(E,B)=(gc(E,B)+gs(E,B)+gbw(E,B))/numEs=(2+10+2)/1=14
总结 B 的邻居节点的 g ( m , n ) g(m,n) g(m,n)值和 ( g ( m , n ) ∗ n u m m a , n u m m a ) (g(m,n)*num_m^a, num_m^a) (g(m,n)∗numma,numma)对
- 节点 A:
g
(
A
,
B
)
=
13
/
3
g(A,B) = 13/3
g(A,B)=13/3。对应成对值:
(13, 3) - 节点 C:
g
(
C
,
B
)
=
13
g(C,B) = 13
g(C,B)=13。对应成对值:
(13, 1) - 节点 E:
g
(
E
,
B
)
=
14
g(E,B) = 14
g(E,B)=14。对应成对值:
(14, 1)
Step2:贪心部署 EMs
-
选择 g(m,B) 最小的邻居A: A 可以部署3个 EM, 因此部署 EM1, EM2, EM3 到节点A。
- 贡献给 N F C B NFCB NFCB 的成本部分: g ( A , B ) ∗ n u m A s = 13 g(A,B) * num_A^s = 13 g(A,B)∗numAs=13。
- 剩余待部署 EMs: 1个 EM。
-
选择下一个 g(m,B) 最小的邻居C:C 可以部署1个 EM,将EM4 部署到节点 C。
- 贡献给 N F C B NFCB NFCB 的成本部分: g ( C , B ) ∗ n u m C s = 13 g(C,B) * num_C^s = 13 g(C,B)∗numCs=13。
- 剩余待部署 EMs: 0个。
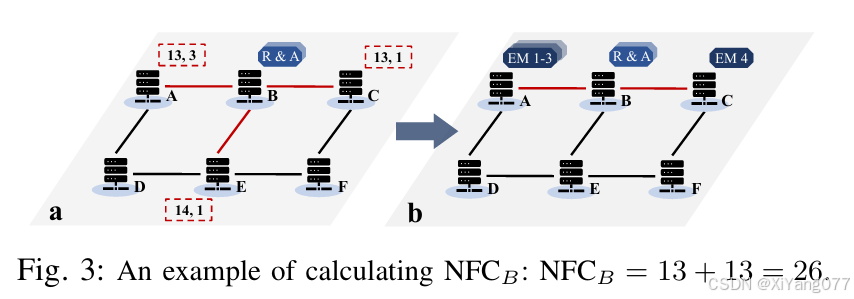
Step3:计算 N F C B NFCB NFCB
N F C B = ( g ( A , B ) ∗ n u m A B ) + ( g ( C , B ) ∗ n u m C B ) + C R ∗ P B C + C A ∗ P B C = ( 13 + 13 ) + = 26 + NFCB = (g(A,B) * num_A^B) + (g(C,B) * num_C^B) +CR * P_B^C + CA * P_B^C=(13+13)+=26+ NFCB=(g(A,B)∗numAB)+(g(C,B)∗numCB)+CR∗PBC+CA∗PBC=(13+13)+=26+























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










