排序 — 归并排序

最新推荐文章于 2024-07-02 13:41:23 发布

朝上

最新推荐文章于 2024-07-02 13:41:23 发布

阅读量231

点赞数

分类专栏： javaSE 文章标签：排序算法算法数据结构

本文链接：https://blog.youkuaiyun.com/m0_51051154/article/details/122930481

版权

javaSE 专栏收录该内容

18 篇文章

订阅专栏

归并排序是一种采用分治法的高效排序算法，其基本思想是将序列拆分成两半，分别排序后再合并。文章通过动图演示和代码实现详细解释了归并排序的过程，包括递归拆分和合并有序子序列。归并排序的平均时间复杂度为O(nlogn)，且稳定性良好。Java中的Arrays.sort()方法使用了优化版的归并排序——TimSort。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.基本思想

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

2.补充:分治法:

在求解一个输入规模为n，而n的取值又很大的问题时，直接求解往往非常困难。这时，可以先分析问题本身所具有的某些特性，然后从这些特性出发，选择某些适当的设计策略来求解。例如，如果把n个输入划分成k个子集，分别对这些子集进行求解，再把所得到的解组合起来，从而得到整个问题的解，这样，有时可以收到很好的效果。这种方法，就是所谓的分治法。
一般来说，分治法是把问题划分成多个子问题来进行处理。这些子问题，在结构上和原来的问题一样，但在规模上比原来的小。如果所得到的子问题相对来说还太大，可以反复地使用分治策略，把这些子问题再划分成更小的、结构相同的子问题。这样，就可以使用递归的方法分别求解这些子问题，并把这些子问题的解组合起来，从而获得原来问题的解。

3.动图演示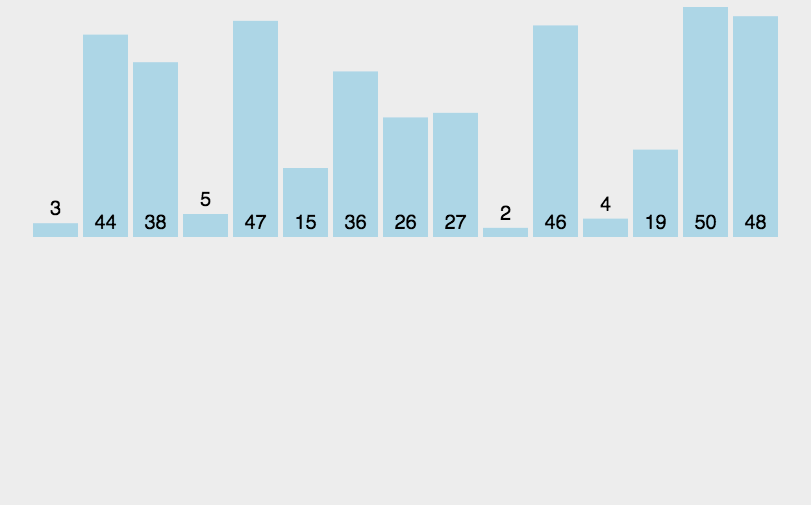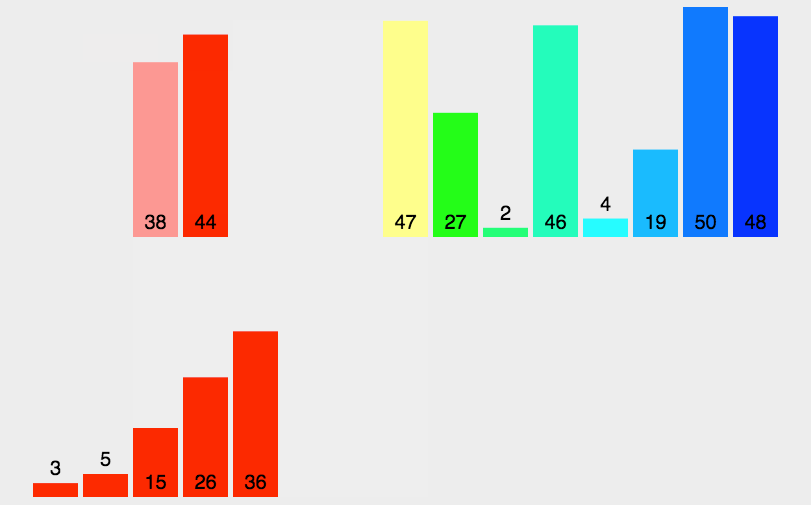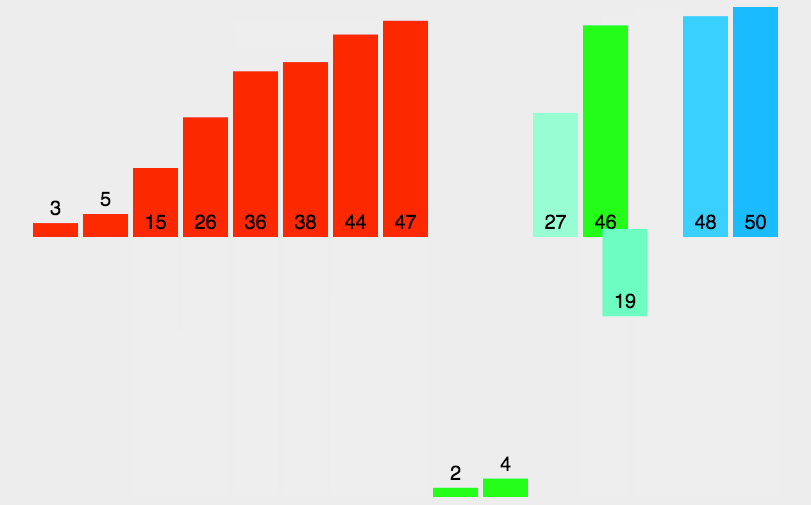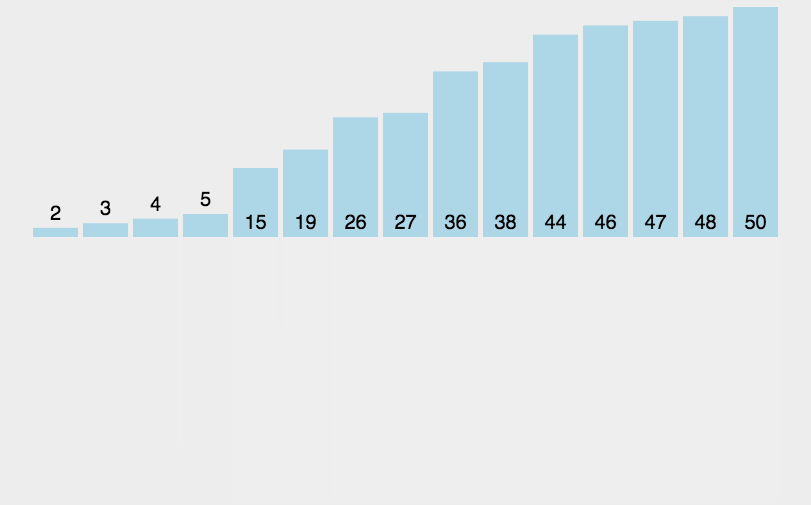

4.算法描述

把长度为n的输入序列分成两个长度为n/2的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。
如图:

在这里插入图片描述

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

在这里插入图片描述

package com.igeek.sort;
import java.util.Arrays;
public class MergeSort {
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;//
            sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针(指针就是一个保存了对象的存储地址的变量)->index;
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

总结

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。