齐次的通解+非齐次的特解=非齐次的通解
非齐次的特解可以带入非齐次微分方程中,得到对应的系数。
分布函数的充要条件

它是充要条件也是性质,可以利用性质来解分布函数的参数问题。
概率密度的充要条件

正态分布的一些公式

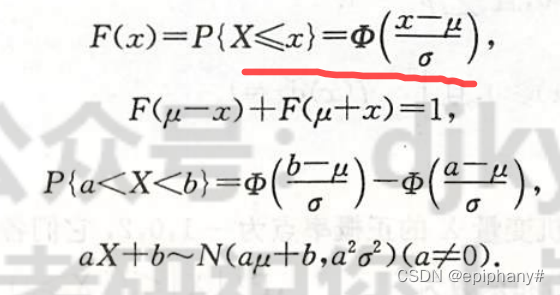
其中 x为偶函数
正太分布的推导
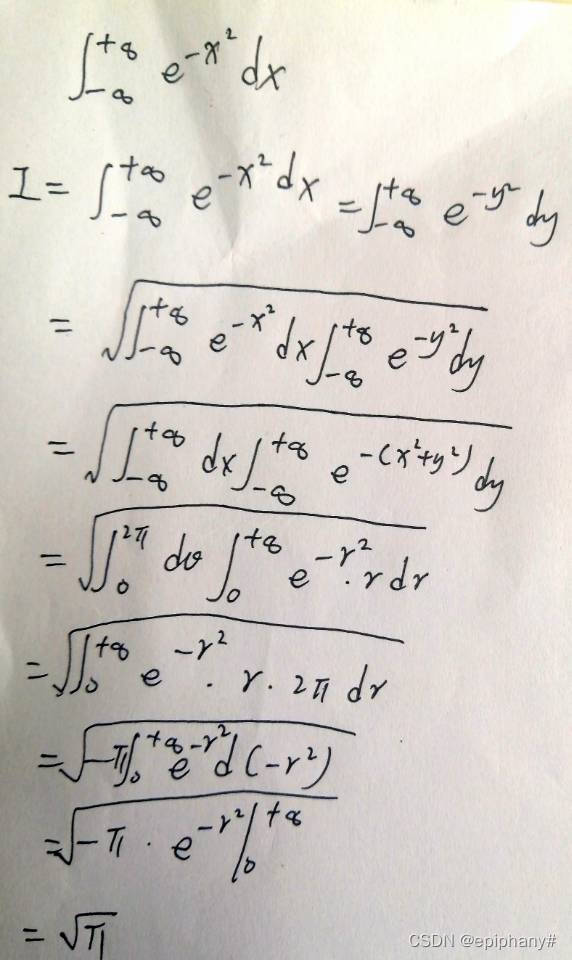
二项分布

泊松分布


指数分布具有无记忆性
-------------------4.2--------------------------
边缘概率密度

条件概率密度

数学期望 的性质


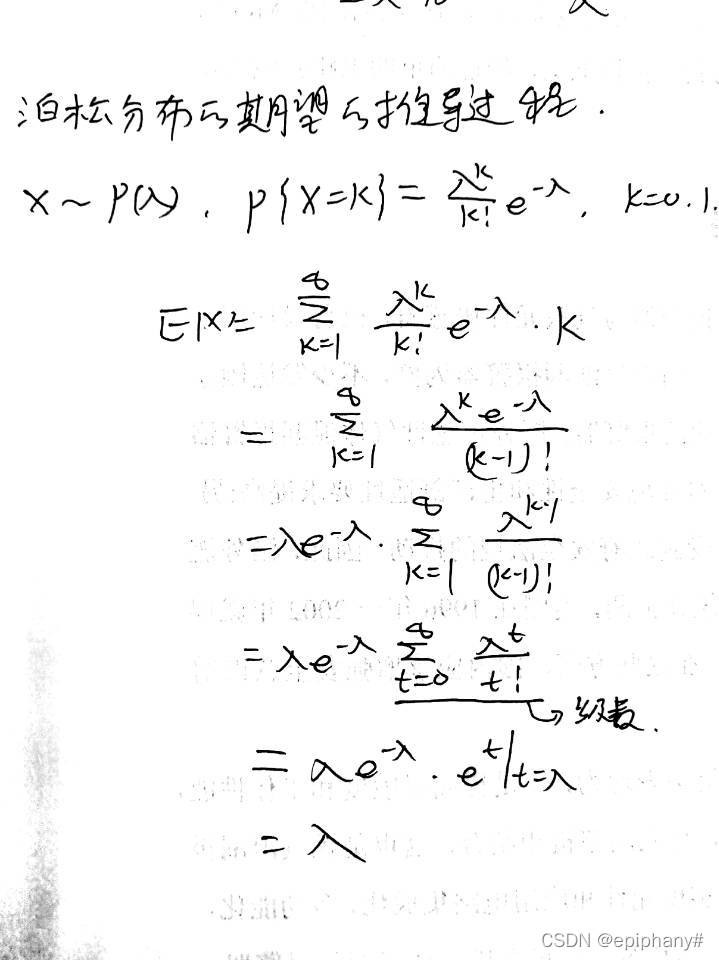

齐次的通解+非齐次的特解=非齐次的通解
非齐次的特解可以带入非齐次微分方程中,得到对应的系数。
分布函数的充要条件

它是充要条件也是性质,可以利用性质来解分布函数的参数问题。
概率密度的充要条件

正态分布的一些公式

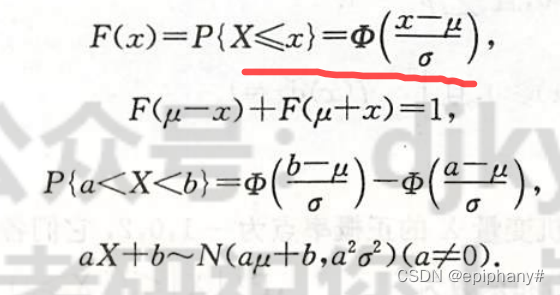
其中 x为偶函数
正太分布的推导
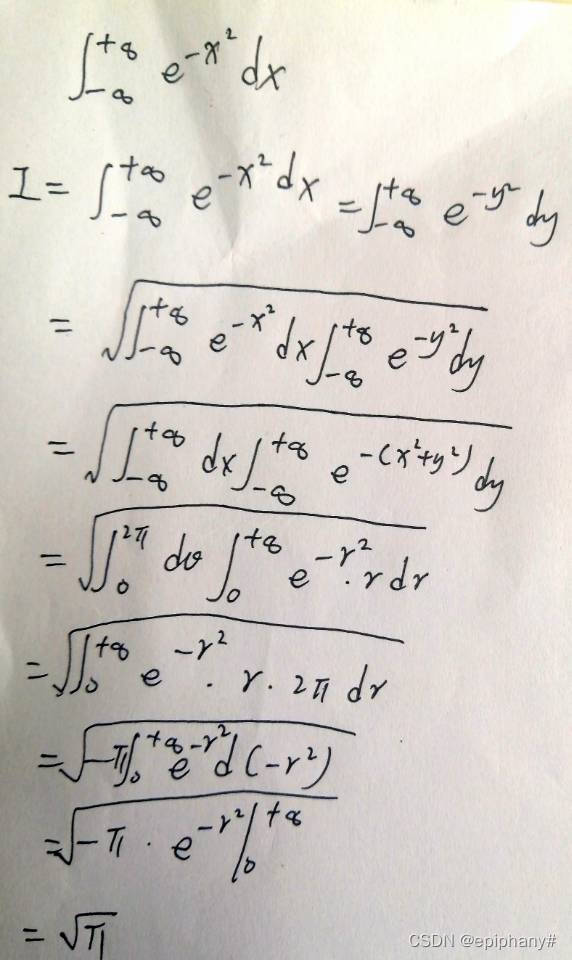
二项分布

泊松分布


指数分布具有无记忆性
-------------------4.2--------------------------
边缘概率密度

条件概率密度

数学期望 的性质


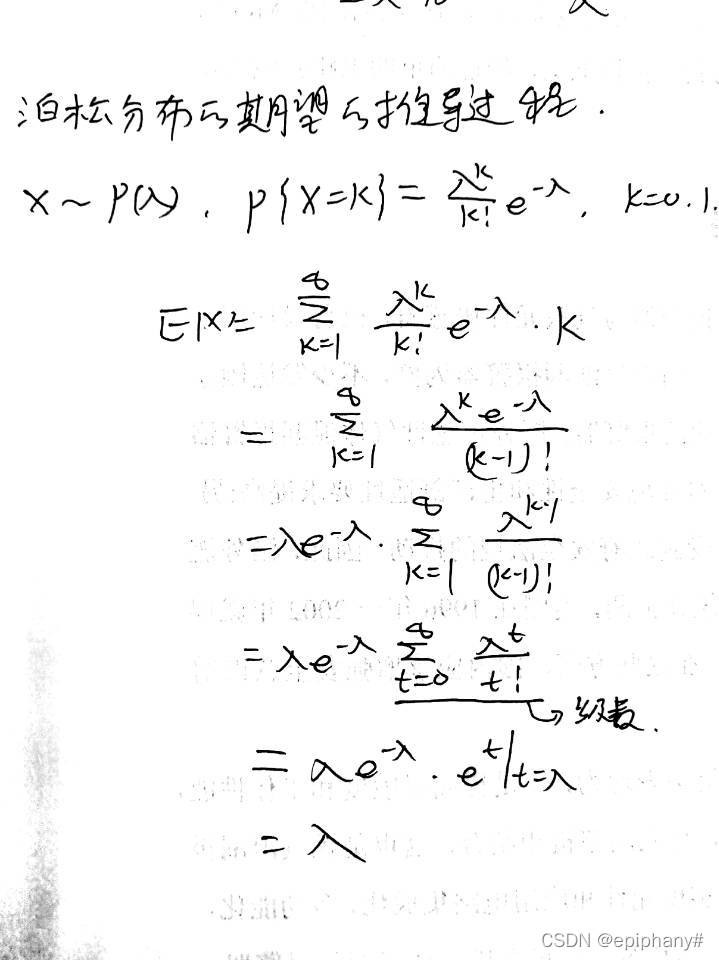


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


