注:整理自李宏毅的课程,可能有部分理解不对,请大家指出!谢谢!
regression : 给出输入,输出得到一个确定的值,可以理解为”定量”。
classification :给出选择,函数输出正确的选择。可以理解为“定性”。
这两者都属于监督学习—对于输入数据X能预测变量Y
无监督学习—从数据X中能发现什么
domain knowledge—专业领域的知识,在机器学习中很需要。比如你根据你的领域知识,认为预测模型的函数是线性的,于是设定函数为y= wx +b 这里的y是你要预测的 x是已经有的数据 而你判断呈一个线性关系,然后去训练这个模型得到参数w与b 这里面的判断就是根据你的domain knowledge
什么是模型?(这个词在机器学习中经常看到)
Model—Function with Unknown Parameters
模型——带有未知参数的函数就叫做模型
比如上面那个y = wx +b 就是一个模型【一个线性模型 Linear Model】
其中x是 feature w 是 weight b 是 bias
什么是Loss—损失函数
上面的模型对应一个损失函数:L(b,w) 反映这个模型与实际情况的误差情况 损失函数的计算公式不一样,人为设定
什么是最优化Optimization
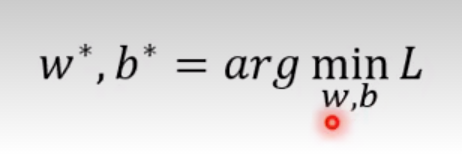
——找一个w*,b*出来,使得平均损失函数最小 李宏毅第一节课提出了一个Gradient Decent的优化方法
梯度下降(Gradient Descent)是一种常用的优化算法,用于最小化损失函数或目标函数。它是机器学习和深度学习中最基本的优化方法之一。
梯度下降的目标是通过迭代的方式找到损失函数的最小值或目标函数的最小值。在梯度下降中,我们首先计算损失函数关于参数的梯度(即导数),然后沿着梯度的反方向更新参数,使损失函数逐渐减小。
具体来说,梯度下降的步骤如下:
(1)初始化参数:选择初始参数的值。
(2)计算梯度:计算损失函数关于参数的梯度(导数),表示损失函数在当前参数值处的变化率。
(3)更新参数:沿着梯度的反方向更新参数值,通常是通过将当前参数值减去学习率(learning rate)乘以梯度。
重复步骤2和步骤3,直到满足停止准则,如达到最大迭代次数或损失函数的变化很小。
什么是学习率?
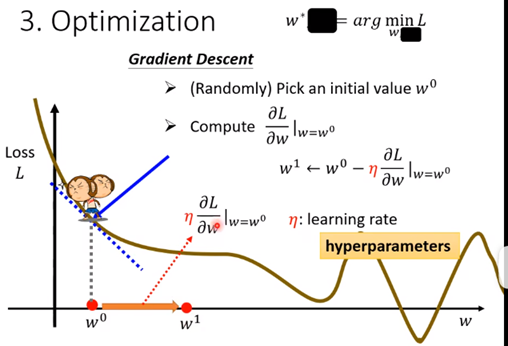
如图,当去w0时,发现w往右边走的时候Loss会减小(根据斜率判断往哪边走),所以走到w1去
而怎么确定走多少呢,取决于两个东西:(1)斜率大小(2)设置的学习率η 如图红箭头指向的公式
具体来说 就是这个公式:
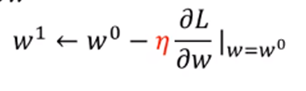
这就是初步认识所谓的【调参】
Gradient Decent 有local minimal的问题 即类似于函数中的最小值和极小值的问题,可能你的机器学习到了极小值 就停止训练学习了 但是实际上存在一个更小的损失函数值
上面是一个参数的例子,如果是两个参数(如笔记上面最先提出的模型)那么就是对两个参数分别求斜率:,经过调整使他们逼近于0:
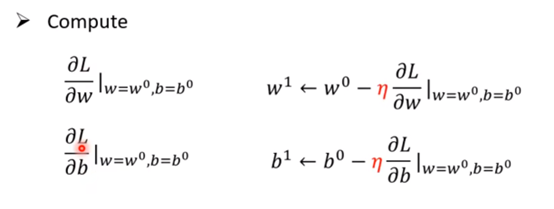





 本文介绍了监督学习(回归与分类)的区别,强调了领域知识在模型设定中的作用,讲解了模型、损失函数和最优化的概念,重点阐述了梯度下降算法作为优化方法,以及学习率在调整参数过程中的关键作用,同时提到了局部最小问题及其解决方案。
本文介绍了监督学习(回归与分类)的区别,强调了领域知识在模型设定中的作用,讲解了模型、损失函数和最优化的概念,重点阐述了梯度下降算法作为优化方法,以及学习率在调整参数过程中的关键作用,同时提到了局部最小问题及其解决方案。
















 2470
2470

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








