2020多校联赛第六场E题：Easy Construction

原创于 2020-08-02 09:14:18 发布 · 180 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

2020多校联赛专栏收录该内容

14 篇文章

订阅专栏

本文探讨了如何构造一个整数n的全排列，使得任意长度i的子区间之和模n余k。文章提供了判断解的存在性和具体构造方法，包括奇数和偶数情况下的不同策略。

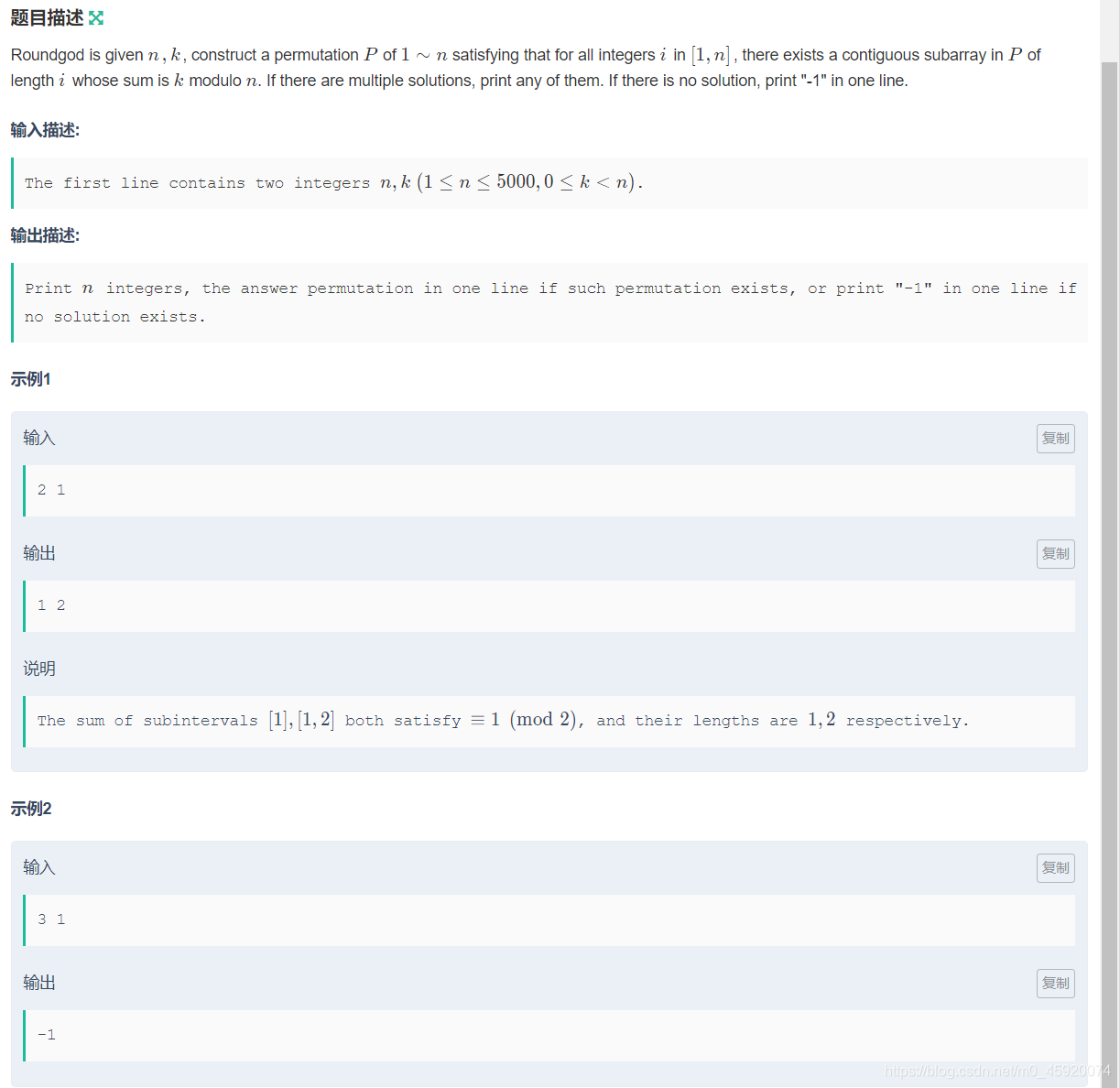
题意：
给出n,k，构造出一个n的全排列P，使得对于 1~n 中任意的数 i，P 都存在一个长为 i 的子区间，其和模 n 余 k。有解输出任意一组，无解输出 -1。
思路：
如果1-n的总和(n(n+1)/2)%n == k，那么就一定有解决方案。当n为奇数时，1-n的和必定是n的倍数，即k一定为0；而当n为偶数时，k一定为n/2。
如果一定有解决方案，那么如何构造这样一个排列也是一个问题。
如果n%2 == 1，那么k=0，令P={n,1,n-1,2,n-2,…}。
如果n%2 == 0，那么k=n/2，令P={n,n/2,1,n-1,2,n-2,…}。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    if(n%2)
    {
        if(!k)
        {
            for(int i=1;i<=n/2;i++) printf("%d %d ",i,n-i);
            printf("%d",n);
        }
        else printf("-1");
    }
    else
    {
        if((n*(n+1)/2)%n==k)
        {
            for(int i=1;i<n/2;i++) printf("%d %d ",i,n-i);
            printf("%d %d",n/2,n);
        }
        else printf("-1");
    }
    return 0;
}