1:马尔科夫无向图
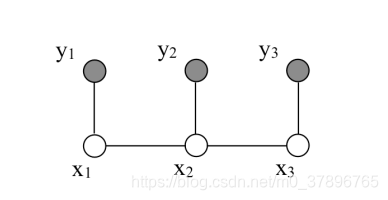
在 上面的无向图中,我们有观测变量和隐变量,是一种较简单的马尔科夫结构,3个观测变量y,3个隐藏变量x,
通过因子图的方式联合概率可以写为:
p(x1,x2,x3,y1,y2,y3)=ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)p(x_1,x_2,x_3,y_1,y_2,y_3)=\phi(x_1,x_2)\phi(x_2,x_3)\psi(x_1,y_1)\psi(x_2,y_2)\psi(x_3,y_3)p(x1,x2,x3,y1,y2,y3)=ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)
这里ϕ()函数代表隐状态之间的连接函数,ψ()代表观测节点和隐藏节点的函数\phi()函数代表隐状态之间的连接函数,\psi()代表观测节点和隐藏节点的函数ϕ()函数代表隐状态之间的连接函数,ψ()代表观测节点和隐藏节点的函数
因为有:
p(x,y)=p(x∣y)p(y)p(x,y)=p(x|y)p(y)p(x,y)=p(x∣y)p(y)
p(x1,x2,x3,y1,y2,y3)=p(x1,x2,x3∣y1,y2,y3).p(y)p(x_1,x_2,x_3,y_1,y_2,y_3)=p(x_1,x_2,x_3|y_1,y_2,y_3).p(y)p(x1,x2,x3,y1,y2,y3)=p(x1,x2,x3∣y1,y2,y3).p(y)
所以:
p(x1,x2,x3∣y1,y2,y3)=1p(y)p(x1,x2,x3,y1,y2,y3)p(x_1,x_2,x_3|y_1,y_2,y_3)=\displaystyle \frac{1}{p(y)}p(x_1,x_2,x_3,y_1,y_2,y_3)p(x1,x2,x3∣y1,y2,y3)=p(y)1p(x1,x2,x3,y1,y2,y3)
p(x1,x2,x3∣y1,y2,y3)=1p(y)ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)p(x_1,x_2,x_3|y_1,y_2,y_3)=\displaystyle \frac{1}{p(y)}\phi(x_1,x_2)\phi(x_2,x_3)\psi(x_1,y_1)\psi(x_2,y_2)\psi(x_3,y_3)p(x1,x2,x3∣y1,y2,y3)=p(y)1ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)
p(x∣y)=1p(y)∏i,jϕ(xi,xj)∏iψ(xi,yi)p(x|y)=\displaystyle \frac{1}{p(y)}\prod_{i,j}\phi(x_i,x_j) \prod_i \psi(x_i,y_i)p(x∣y)=p(y)1i,j∏ϕ(xi,xj)i∏ψ(xi,yi)
这里的i和j是空间上的邻居,并且是联通的这里的i和j是空间上的邻居,并且是联通的这里的i和j是空间上的邻居,并且是联通的
2:图模型中的推断问题
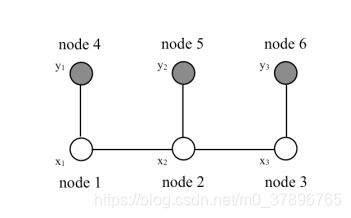
计算上图的边缘概率
P(x1∣y)=∑x2∑x3P(x1,x2,x3∣y)P(x_1|y)=\displaystyle \sum_{x_2} \sum_{x_3}P(x_1,x_2,x_3|y)P(x1∣y)=x2∑x3∑P(x1,x2,x3∣y)
如果对结构一无所知的话,直接计算,计算量是指数级别的,计算将变得非常困难
但是在我们知道是马尔科夫结构的情况下,就可以使用因子分解的方式代替上面的公式
p(x1∣y)=1p(y)∑x2∑x3ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)p(x_1|y)=\displaystyle \frac{1}{p(y)}\sum_{x_2} \sum_{x_3}\phi(x_1,x_2)\phi(x_2,x_3)\psi(x_1,y_1)\psi(x_2,y_2)\psi(x_3,y_3)p(x1∣y)=p(y)1x2∑x3∑ϕ(x1,x2)ϕ(x2,x3)ψ(x1,y1)ψ(x2,y2)ψ(x3,y3)
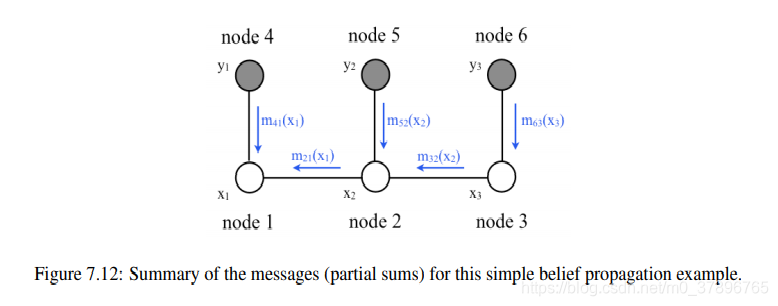
下一步展示的是belief propagation的主要思想:因为联合概率是模块化的,
并不是每个变量都耦合到其他的变量上面,因此可以只把对应的求和符号放在
相关的变量前面,这样计算结果相同,但是计算量却少很多
(我们标记子序列为消息m,同时x1,x2,x3,y1,y2,y3标记为node1到node6)(我们标记子序列为消息m,同时x_1,x_2,x_3,y_1,y_2,y_3标记为node1到node6)(我们标记子序列为消息m,同时x1,x2,x3,y1,y2,y3标记为node1到node6)
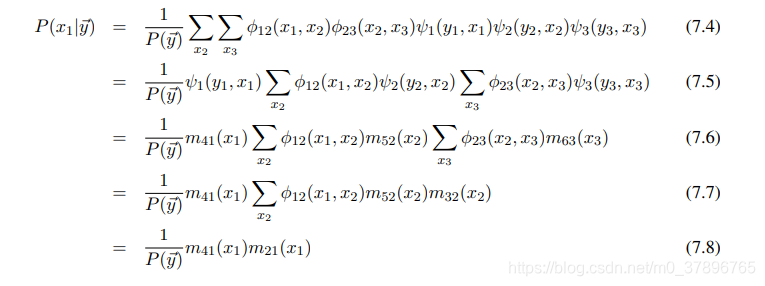
这里我们定义下列消息术语:
m41=ψ1(y1,x1)m_{41}=\psi_1(y_1,x_1)m41=ψ1(y1,x1)
m52=ψ1(y2,x2)m_{52}=\psi_1(y_2,x_2)m52=ψ1(y2,x2)
m63=ψ1(y3,x3)m_{63}=\psi_1(y_3,x_3)m63=ψ1(y3,x3)
m32=∑x3ϕ23(x2,x3)m63(x3)m_{32}=\displaystyle \sum_{x_3}\phi_{23}(x_2,x_3)m_{63}(x_3)m32=x3∑ϕ23(x2,x3)m63(x3)
m21=∑x2ϕ12(x1,x2)m63(x3)m_{21}=\displaystyle \sum_{x_2}\phi_{12}(x_1,x_2)m_{63}(x_3)m21=x2∑ϕ12(x1,x2)m63(x3)
这样计算量将从原来的xnx^nxn降为n2n^2n2,很明显通过这种方式使得计算成为可能
下面我们计算另外一个分量的边缘概率
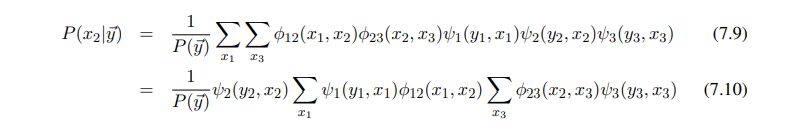
对比7.5,这里再一次需要计算部分和:
∑x3ϕ23(x2,x3)m63(x3)\displaystyle \sum_{x_3}\phi_{23}(x_2,x_3)m_{63}(x_3)x3∑ϕ23(x2,x3)m63(x3)
belief propagation能够自动的把这些部分和缓存起来给其他的概率计算使用
这些重复利用的部分和称作 “消息”
3:Belief propagation (BP)
BP算法描述:
3.1:消息传递规则
消息的参数是状态节点,这些节点是消息要到达的
为了计算从节点j到节点i的消息为了计算从节点j到节点i的消息为了计算从节点j到节点i的消息:
- 把所有到达节点j的消息联乘,除了从节点i返回给节点j的消息把所有到达节点j的消息联乘,除了从节点i返回给节点j的消息把所有到达节点j的消息联乘,除了从节点i返回给节点j的消息
- 再乘以兼容性函数ϕi,j(xi,xj)再乘以兼容性函数\phi_{i,j}(x_i,x_j)再乘以兼容性函数ϕi,j(xi,xj)
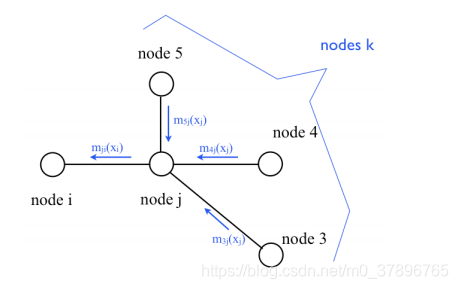
上图展示了消息从节点j到节点i的传递过程上图展示了消息从节点j到节点i的传递过程上图展示了消息从节点j到节点i的传递过程
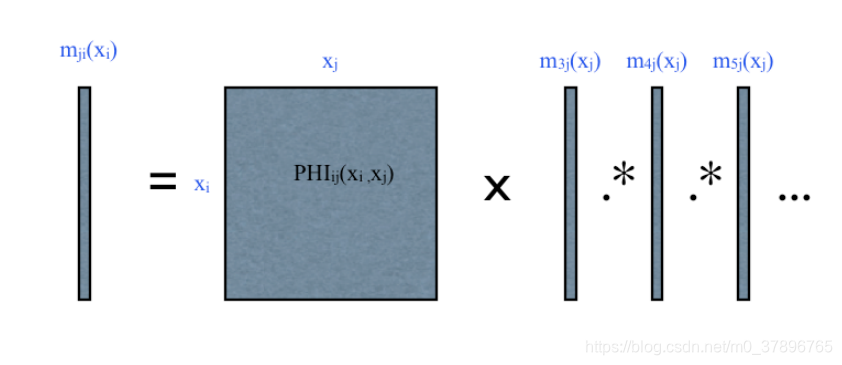
上图使用矩阵和向量的方式展示消息公式
举例:
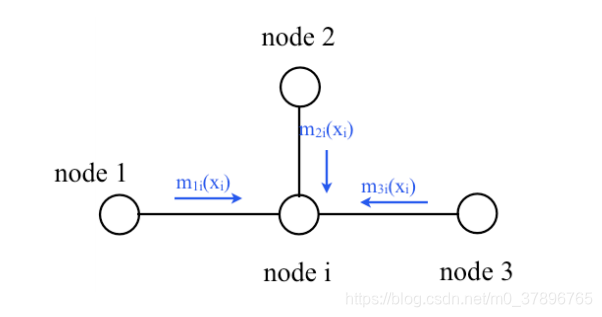
对于上图中求节点i的概率有:
p(xi)=∏mj,i(xi)p(x_i)=\prod m_{j,i}(x_i)p(xi)=∏mj,i(xi)
- 求边缘概率xi,通过求和把xj去掉求边缘概率x_i,通过求和把x_j去掉求边缘概率xi,通过求和把xj去掉
mj,i(xi)=∑xjϕ(xi,xj)∏k∈η(j)mk,j(xj)m_{j,i}(x_i)=\displaystyle \sum_{x_j}\phi(x_i,x_j) \prod_{k \in \eta(j)} m_{k,j}(x_j)mj,i(xi)=xj∑ϕ(xi,xj)k∈η(j)∏mk,j(xj)
这里η(j)表示节点j的邻居\eta (j)表示节点j的邻居η(j)表示节点j的邻居
3.2 :边缘概率
一个节点的边缘概率是所有进入该节点消息的联乘
Pi(xi)=∏j∈η(i)mj,i(xi)P_i(x_i)=\displaystyle \prod_{j \in \eta(i)} m_{j,i}(x_i)Pi(xi)=j∈η(i)∏mj,i(xi)
\quad
4:BP算法描述
BP=变量消除+cache
BP:
- get root node :获取root节点
- collect message :收集消息
for xix_ixi in nb(root)
collect message(xix_ixi) - distribute message:分发消息
for xjx_jxj in nb(root)
distribute message(xjx_jxj)







 本文深入探讨了马尔科夫无向图的结构与特性,详细解析了观测变量与隐变量的关系,以及如何通过因子图表示联合概率。文章进一步介绍了Belief Propagation(BP)算法,讲解了其消息传递规则与边缘概率计算,展示了如何通过BP算法有效减少计算复杂度。
本文深入探讨了马尔科夫无向图的结构与特性,详细解析了观测变量与隐变量的关系,以及如何通过因子图表示联合概率。文章进一步介绍了Belief Propagation(BP)算法,讲解了其消息传递规则与边缘概率计算,展示了如何通过BP算法有效减少计算复杂度。
















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








