数据挖掘学习--逻辑回归3

1.前言

前文所讲的逻辑回归也将逻辑回归再建模时的一些问题学习了解决的方法，我在本文讲一下为何需要逻辑回归来代替线性回归呢？以及另外一个问题，逻辑回归的实际应用能力问题----单纯的逻辑回归只能应用于二分类问题，该如何处理？

2.逻辑回归代替线性回归

为什么要用逻辑回归来代替线性回归呢？我们首先要明确的是逻辑回归是一种分类器，它总的来讲是要达到我们输入一个带预测的向量后，经过模型的计算输出这个向量所属于的类别。那么我们考虑单纯的线性回归，就会有这样的式子：

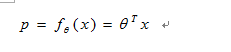
这样得到的p值也就是概率值，我们预想中它是再[0 ，1]取值，但是这样由右边计算出来的值就可能超过这个范围，为我们分类增加了很大的难度。
此时就有人提出了sigmod函数：

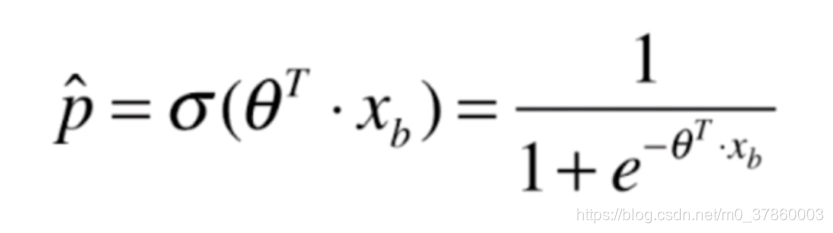
不难发现，sigmoid函数图像是这样的：

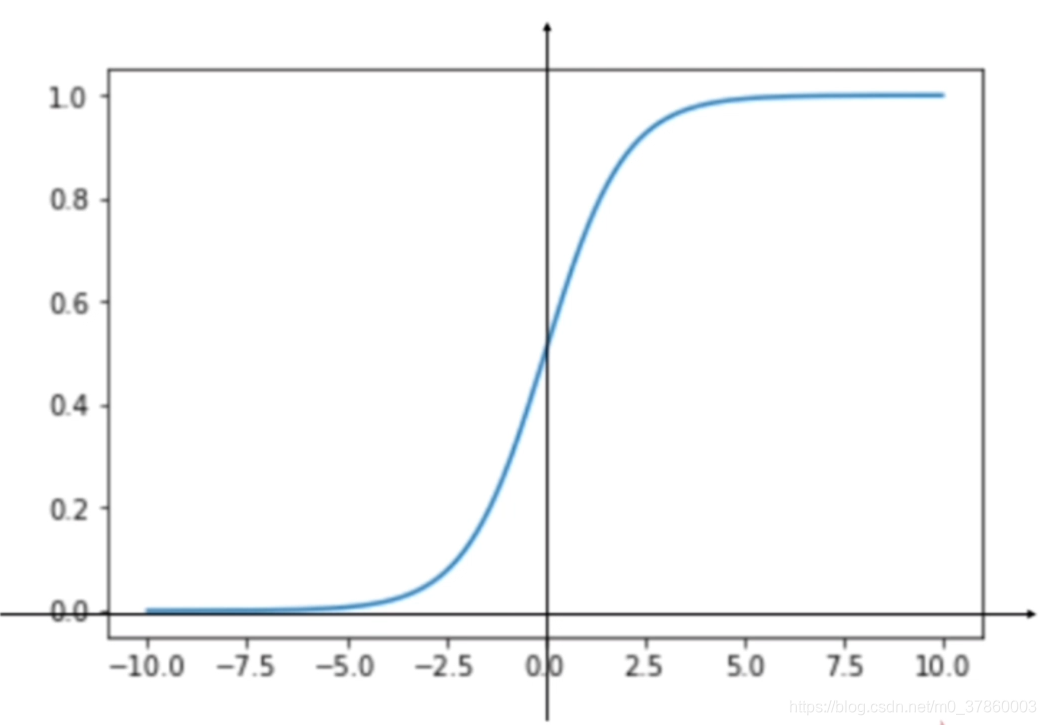
就将右式的值相对应的（不损失相对大小的情况下）转化为值域为[0 , 1]的值，再通过确定好的规则进行分类。
套用了一层函数的线性回归函数，就是逻辑回归（注意，逻辑回归的损失函数和线性回归的损失函数是不一样的，这是因为线性回归求的是回归值，而逻辑回归求的是概率值）。

3.单纯逻辑回归出现的问题

单纯的逻辑回归只能应用于二分类问题，原因就在于既定的规则是：

面对实际问题时，我们就自然而然的会想实际的分类问题肯定有不止是二分类问题的情况。面对这样的场景，就有两种变化的逻辑回归算法来解决：One vs Rest 以及 One vs One

（1）.One vs Rest方法：

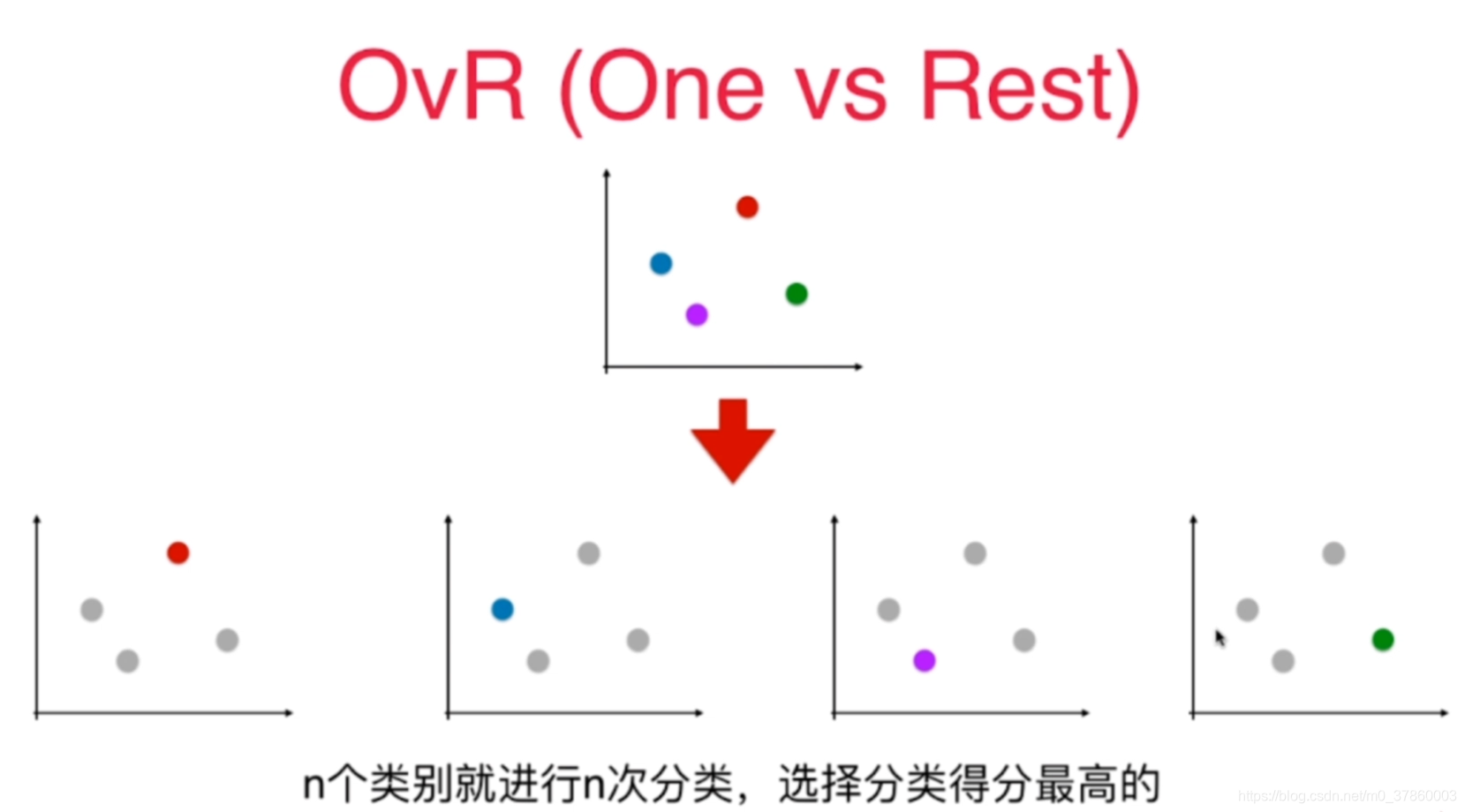
面对每个不同类别的样本点，拆分成n次分类，对每次分类就是本样本点和其余所有样本点（此时其他样本点看作一类）进行二分类，那么这样就是变成了多个二分类问题，最后选择分类得分最高的那个。
特点：耗时短，但准确度低

（2）.One vs One方法：

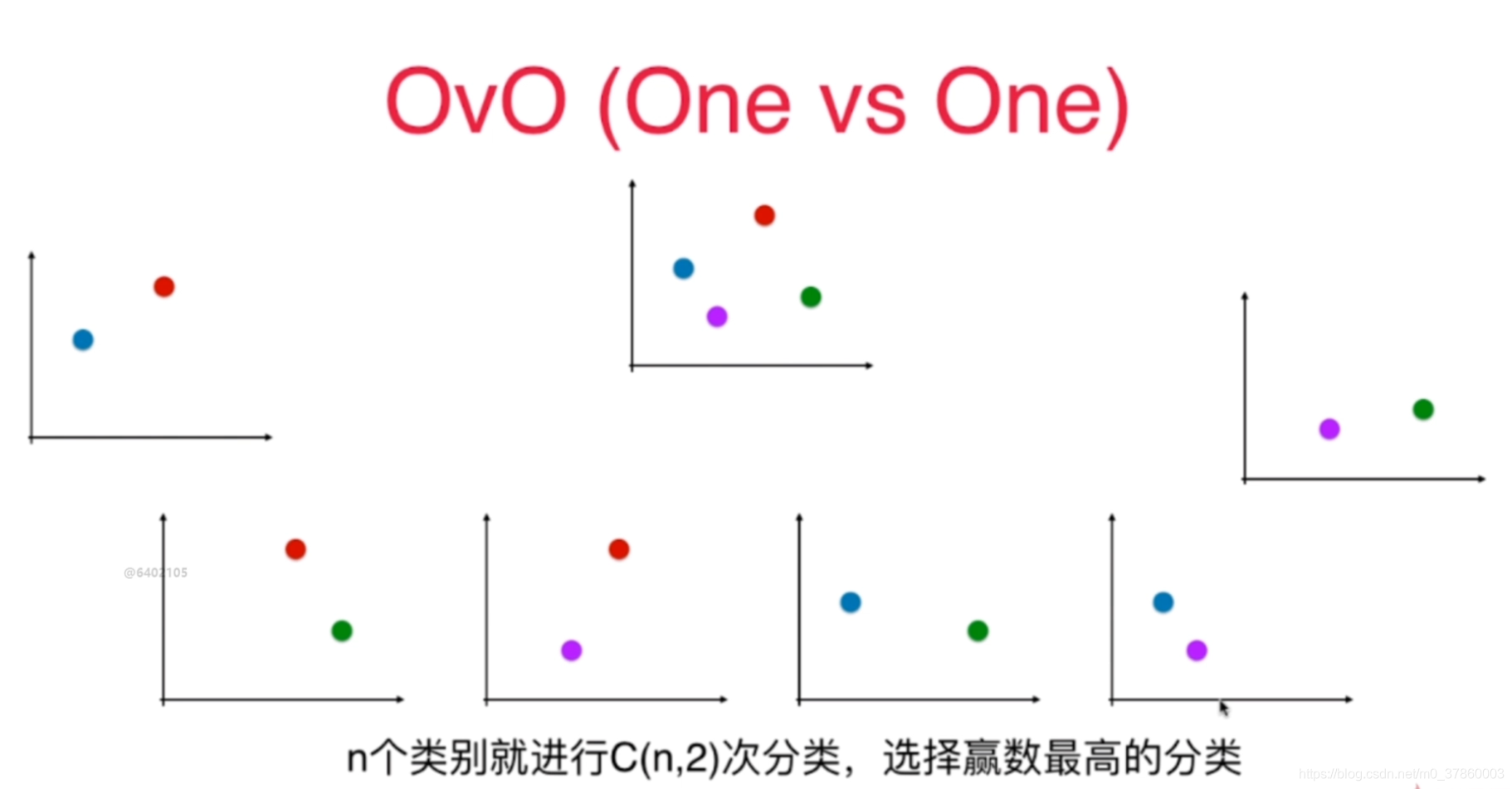
一对一的二分类，每一个样本都和其他样本进行一次二分类，选择赢数最高的分类。
特点：耗时长（O(n2)级别的时间复杂度），更准确

4.ovr和ovo再sklearn的实现代码

#用ovr的多分类逻辑会及方法
log_reg1 = LogisticRegression(multi_class='ovr')
log_reg1.fit(x_train , y_train)

#用ovo的多分类逻辑回归方法
log_reg2 = LogisticRegression(multi_class='multinomial' , solver='newton-cg')
log_reg2.fit(x_train , y_train)