入门人工智能·机器学习篇·概率分布（AIML04）

文章内容参考《PATTERN RECOGNITION & MACHINE LEARNING》作者：CHRISTOPHER M.BISHOP 文章作者联系邮箱：humminwang@163.com

Preview (Chapter 2):

• 二元变量$\leftarrow$
• 多元变量$\leftarrow$
• 高斯分布
• 指数族
• 无参方法

---

1 二值变量

1.1 伯努利分布

举例：一次抛硬币结果$heads=1,tails=0$：
$$p(x=1|\mu )=\mu$$
由此可知抛硬币结果正反面存在一种分布，这种非0即1的单次实验被称为伯努利分布。也称为零一分布、两点分布。
伯努利分布：
$$Bern(x|\mu )={\mu }^x(1-\mu {)}^{1-x}$$
其中期望、方差为$E[\mu ]=\mu ,Var[x]=\mu (1-\mu )$。

1.2 二项分布

举例：10次抛硬币，5次出现正面的概率？
二项分布是n个独立的是/非试验中成功的次数的离散概率分布。其实就是重复n次独立的伯努利试验。则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布也就是伯努利分布。
$$Bin(m|N,\mu )=C_N^m{\mu }^m(1-\mu {)}^{N-m}$$
m表示成功的次数，$\mu$成功的概率。
期望、方差为$E[m]={\sum }_{m=0}^{N}Bin(m|N,\mu )=N\mu ,Var[m]={\sum }_{m=0}^N(m-E[m]{)}^{2}Bin(m|N,\mu )=N\mu (1-\mu )$。

更多分布参考博客：

https://blog.youkuaiyun.com/m0_37846020/article/details/88838885

1.3 参数估计

对于分布中的未知参数，根据统计学的知识，在点估计中估计参数，可以利用最大似然估计算法（MLE）。
举例对于未知的伯努利分布，比如我们抛一个硬币N次：
数据： D = { x 1 , x 2 , . . . , x N } D=\{x_1,x_2,...,x_N\} D={x1​,x2​,...,xN​},$m$个正面，$N-m$个反面,所以我们可以得到：
$$p(D|\mu )=\prod _{n=1}^{N}p(x_n|\mu )=\prod _{n=1}^N{\mu }^{x_n}(1-\mu {)}^{1-x_n}$$
之后对似然函数求去对数：
l n p ( D ∣ μ ) = ∑ n = 1 N l n p ( x n ∣ μ ) = ∑ n = 1 N { x n l n μ + ( 1 − x n ) l n ( 1 − μ ) } lnp(D|\mu)=\sum_{n=1}^Nlnp(x_n|\mu)=\sum_{n=1}^N\{x_nln\mu+(1-x_n)ln(1-\mu)\} lnp(D∣μ)=n=1∑N​lnp(xn​∣μ)=n=1∑N​{xn​lnμ+(1−xn​)ln(1−μ)}
$${\mu }_{ML}=\frac{1}{N}\sum _{n=1}^N{x}_n$$
经典的最大似然法求参数产生的问题：
如果样本不平衡，很可能造成过拟合。
D = { 1 , 1 , 1 } → μ M L = 3 3 = 1 D=\{1,1,1\}\rightarrow\mu_{ML}=\frac{3}{3}=1 D={1,1,1}→μML​=33​=1

1.4 Beta 分布

贝塔分布$（BetaDistribution)$是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在概率论中，$\beta$分布，也称Β分布，是指一组定义在(0,1) 区间的连续概率分布。
$$Beta(\mu |a,b)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}{\mu }^{a-1}(1-\mu {)}^{b-1}$$
其中期望和方差为$E[\mu ]=\frac{a}{a+b},Var[\mu ]=\frac{ab}{(a+b{)}^2(a+b+1)}$
如果找到一个先验分布$p(\mu )$，利用该先验分布求取的后验分布和先验分布有同样的函数形式，那么我们称为共轭分布。

1.5 贝叶斯下的伯努利分布

在此我们选取似然函数为一个二项分布，${\mu }^{x_n}(1-\mu {)}^{1-x_n}$,参数$\mu$服从$Beta(\mu )$,于是我们可以得到：

所以对伯努利分布来说$Beta$分布提供了一个共轭先验。同时我们可以知道随着数据集大小的增加，$a_N$趋近于$m$,$b_n$将趋近于$N-m$.同时：

在后验概率下的预测：

2 多值变量

考虑一个变量有多个维度，比如$x=(0,0,1,0,0,0{)}^T$。x的分布是：
$$p(x|\mu )=\prod _{k=1}^K{\mu }_k^{x_k}$$
$\sum {\mu }_k=1$,这个分布可以理解为多结果的伯努利分布。

2.1 参数估计

给出数据 D = { x 1 , x 2 , . . . , x N } D=\{x_1,x_2,...,x_N\} D={x1​,x2​,...,xN​},最大似然函数为:

其中$m_k$可以表示为有多少观察值中$x_k=1$，在这个分布中，$m_k$可以称为充分统计量。同时确保${\sum }_k{\mu }_k=1$,引入拉格朗日乘子，$\lambda$:

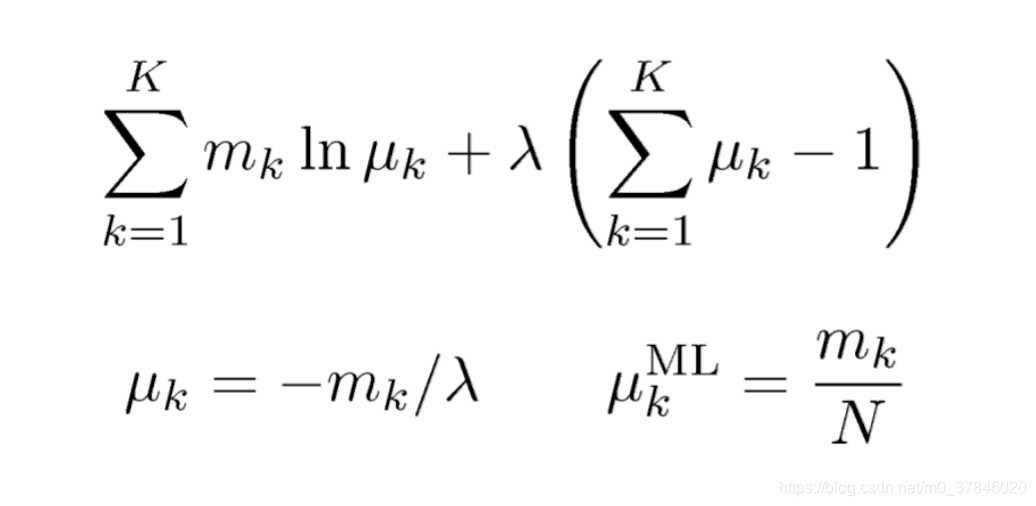
2.2 多项分布

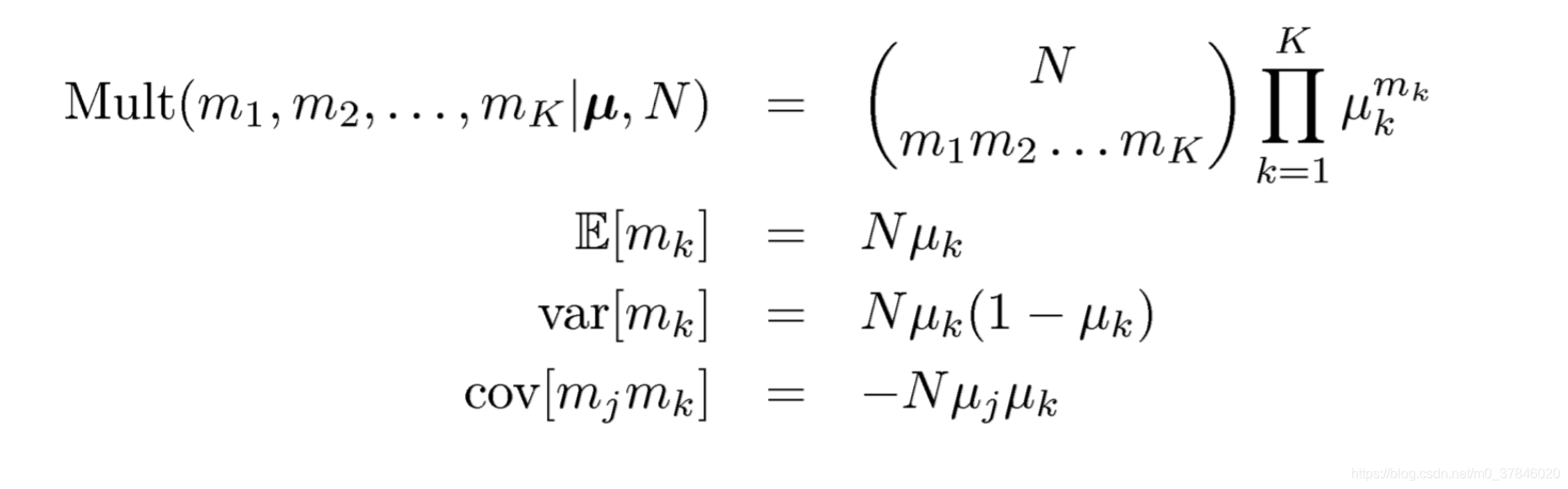
其中$C_N^{m_1...m_k}$代表的含义是将$N$个物体分成$K$个组的个数，每个组大小为$m_1,m_2,.....,m_k$.

2.3 狄利克雷分布

就像之前寻找二项分布的共轭分布Beta分布一样，我们想找到一个和多项分布共轭的分布。狄利克雷分布便是满足该条件。

2.4 贝叶斯下的多项分布