毕业论文使用的卡方检验该如何分析？

一、卡方检验基本说明

有时，在研究中某个随机变量是否服从某种特定的分布是需要进行检验的。可以根据以往的经验或者实际的观测数据分布情况，推测总体可能服从某种分布函数F（x）。卡方检验就是这样一种用来检验给定的概率值下数据来自同一总体的无效假设方法。通常的卡方检验可以用来研究分析定类数据与定类数据之间的关系情况。
在卡方检验中，通常检验的统计量 χ2 如下：
χ2=∑(A−E)2E=∑i=1k(Ai−Ei)2Ei=∑i=1k(Ai−npi)2npi(i=1,2,3,…,k)
其中A代表某个类别的观察频数，E代表基于H0计算出的期望频数，Ai为i水平的观察频数，Ei为i水平的期望频数，n为总频数，pi为i水平的期望频率。当n比较大时，χ2统计量近似服从k-1个自由度的卡方分布。从公式来讲一般卡方值相对越大越好。

二、卡方检验类别

卡方检验目前SPSSAU提供的方法可以分为5类，其中包括卡方检验、卡方拟合优度、配对卡方、分层卡方以及趋势卡方。其中pearson卡方使用的相对较多。

1、卡方检验

卡方检验SPSSAU可以通过【通用方法】交叉（卡方）进行，也可以通过【医学实验研究】卡方检验进行。二者的区别是【医学实验研究】卡方检验输出更多指标。【通用方法】交叉（卡方）相对使用更多。

2、卡方拟合优度检验

卡方拟合优度检验是一种非参数检验方法，其用于研究实际比例情况，是否与预期比例表现一致，它只针对于类别数据。比如总共收集100份数据，其中男性为48个，女性为52个；在收集数据之前预期男女比例应该是4:6 (40%为男性，60%为女性)，那么预期的比例是否与实际的比例有着明显的差异性。

3、配对卡方

如果是配对数据，并且对比的数据为定类数据，因而需要使用配对卡方检验，从数学角度也能将称呼分为 McNemar检验或者Bowker检验，二者的区别如下：

3、分层卡方

在实际研究中，只研究两个分类变量往往具有局限性，因为混杂因素总是存在，如果不研究混杂因素，结论可能存在偏差。为了解决此问题我们引出了分层卡方检验也称CMH检验。比如是否吸烟（X)与是否生病(Y)的关系时，将性别纳入考虑范畴（即混杂因素,分层项Factor）。

4、趋势卡方

医学研究中，有序定类数据的关系研究 Cochran-Armitage，用于k*2(或2*k)的结构 k为有序定类数据,2指两个类别。

三、SPSSAU卡方检验

由于卡方检验类别过多，所以这里针对常用的卡方检验进行说明。案例简单背景：研究不同学历对是否购买某品牌笔记本电脑是否存在差异。

1、整理数据格式

在做数据分析前，首先要将数据整理成正确的数据格式，满足SPSSAU卡方检验的数据格式一共有两种，一种是常规格式，另一种是加权格式。
常规格式：

卡方检验，x、y都为定类数据，上图为常规格式，一行代表一个样本，一列代表一个属性，将全部的原始数据信息列出即可。
加权格式:

加权数据格式基本只针对全部是定类数据的研究时使用，SPSSAU支持常规格式和加权格式两种数据。常规格式提供所有的原始数据信息，而加权格式只提供汇总数据信息。

2、操作

将整理好的数据格式，上传到SPSSAU系统内，将分析项拖拽到对应分析框中即可。操作如下：

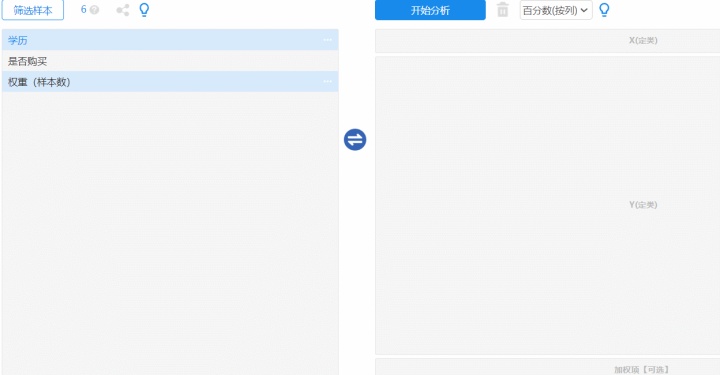
3.卡方检验结果分析

一般流程如下：

从上表分析可知，p值约为0.029小于0.05，所以研究学历对于是否购买笔记本电脑有显著性差异，其中调查者中共有32个人，本科以下的人最多共有12个，本科以上的人最少共有9个，但是总体差异不大，对于本科以下的人其中有10个人，不买该品牌笔记本电脑占比为83.33％，有2个人购买该品牌笔记本电脑占比为16.67％，差异比较明显，不买该品牌笔记本的人较多，对于本科和本科以上学历的人购买该笔记本的人比不买该笔记本人的占比大，由此可见，学历对于是否购买该品牌笔记本有差异性。

接下来我们利用柱状图来分析：

从柱状图也可以看出本科以下学历的人更多不买该品牌电脑，本科和本科以上学历的人更多买该品牌电脑，所以学历对于是否购买该品牌笔记本有差异性。同时也发现本科学历和本科以上学历对于是否购买该品牌笔记本差异性不明显。

来源于：SPSSAU https://zhuanlan.zhihu.com/p/499008852

由于本案例数据为3*2格式，且1 <=E<5格子的比例大于20%（此处为33.33%），因而最终选择使用yates校正卡方值。

补充说明：Pearson卡方和yates校正卡方完全相同是正常现象，多数情况下二者完全相等。

4. 事后多重比较

因为原模型中p值小于0.05具有显著差异性，所以如果有需要可以进一步对分析项进行事后多重比较。

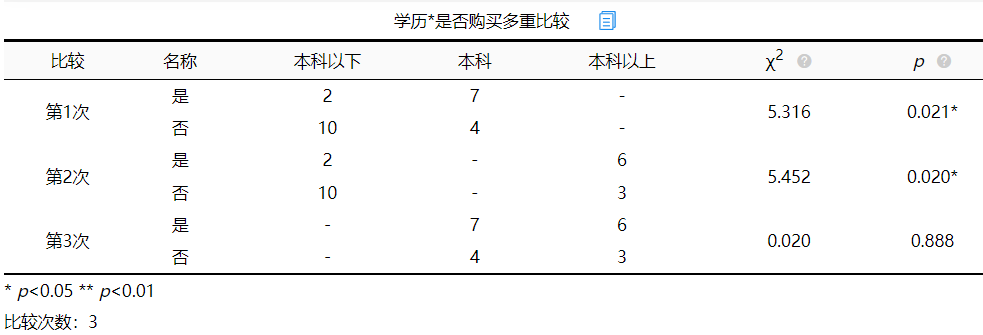
由上表可知，第一次事后多重比较是本科以下学历和本科学历进行比较。发现卡方值为5.316，p值小于0.05具有显著差异性，其中卡方值计算如下：

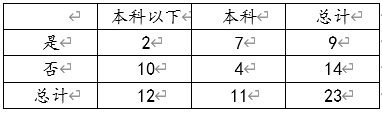
χ2=[(2−9∗12/23)29∗12/23+(7−9∗11/2329∗11/23+(10−14∗12/23)214∗12/23+(4−11∗14/23)211∗14/23]=5.316

第二次事后多重比较是本科以下学历和本科以上学历进行比较。发现p值小于0.05具有显著差异性，同理，第三次比较是本科与本科以上进行比较，p值大于0.05，不具有显著性差异。分析结束。

5、其它应用

其中单选和多选题分析或者多选题和多选题交叉分析可以使用Pearso卡方，如果想要检验各现象百分比是否均匀可以使用卡方拟合优度检验。

参考资料：

多选题分析汇总

6、疑难解惑

如果数据是定量数据怎么进行卡方检验？

定类数据是否能够转化为定量数据一般看两个方面，一种是自身不能转变为定类的，一种是将定量数据转为定类。还有一种是既可以看成定量数据又可以看成定类数据。具体如下：

---

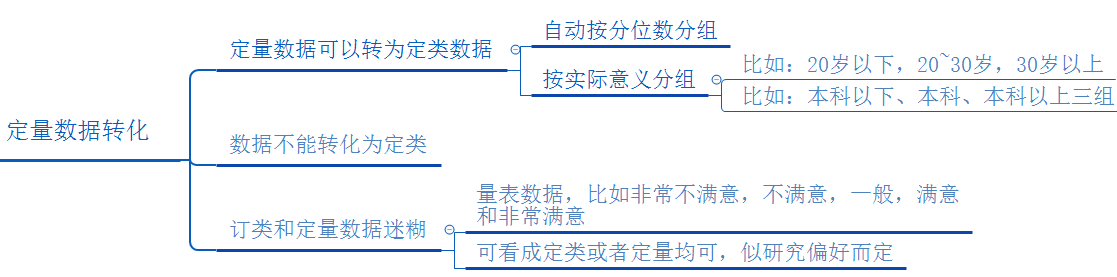
更多干货请登录SPSSAU官网进行查看。

SPSSAUhttps://www.spssau.com/?100001217