闲聊自定义控件之基础——Path

Path在自定义控件里的使用频率也相当的高，使用Path不仅能绘制矩形、圆形等常规图形，还能绘制比较复杂的组合路径。

基本方法

点的相关操作

• moveTo：移动到哪一点
• lineTo：连接到哪一点
• rMoveTo：移动到哪一点（参考点为当前点）
• rlineTo：连接到哪一点（参考点为当前点）
• setLastPoint：设置终点位置
• close：连接开始的点和末尾的点，使路径闭合

图形相关操作

• addRect：在当前Path中添加一个矩形
• addRoundRect：在当前Path中添加一个圆角矩形
• addOval：在当前Path中添加一个椭圆
• addCircle：在当前Path中添加一个圆
• addArc：在当前Path添加一个圆弧
• arcTo：在当前Path添加一个圆弧（会连接上一个操作点）

其它

• offset：对当前Path进行偏移
• reset：清除内容
• rewind：清除内容（保留数据结构）

贝塞尔曲线

这个是个比较烧脑的知识点，因为它需要有一定的数学知识，不过我们大部分情况下只需要理解下其含义，调用Android提供的API即可，三次以上的贝塞尔曲线也很少用到。贝塞尔曲线使得线段或者曲线能够使用数学的方式进行描述，这样就可以方便的在计算机上绘图了。

公式及含义

从百科上给大家摘录了一段关于贝塞尔曲线的讲解

给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。这条线由下式给出：

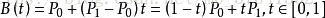
且其等同于线性插值。

二次方公式

二次方贝兹曲线的路径由给定点P0、P1、P2的函数B（t）追踪：

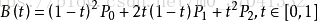
TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。

三次方公式

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。
曲线的参数形式为：

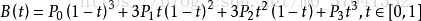
现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝兹样条组成的三次贝兹曲线，用来描绘曲线轮廓。

一般参数公式

阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：

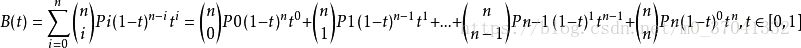
如上公式可如下递归表达： 用表示由点P0、P1、…、Pn所决定的贝兹曲线。

API表现形式

Android中提供