【数据结构】哈夫曼树&哈夫曼编码

哈夫曼树

定义：

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

理解：

举个栗子：假如你有一个衣柜里面有ABCDEF共6件衣服，但是每个衣服穿的频率都是不一样的，54%（问就是喜欢穿），10%，6%，3%，7%，20%
那么现在问题来了，你该怎样把衣服放置才能避免每次找衣服的时候把衣柜搞得一团糟呢？
答案肯定是把频率高的放到里你最近的地方
没错！！哈夫曼树就是这样

下面我们来看看怎样构建一个哈夫曼树来完成这个操作

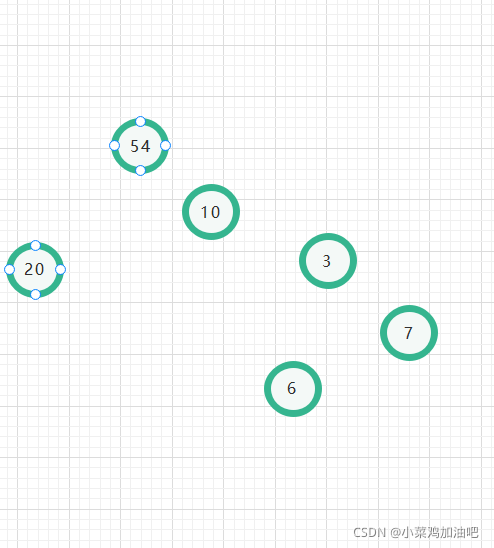
只需要记住一句话：找两个最小的顶点合并

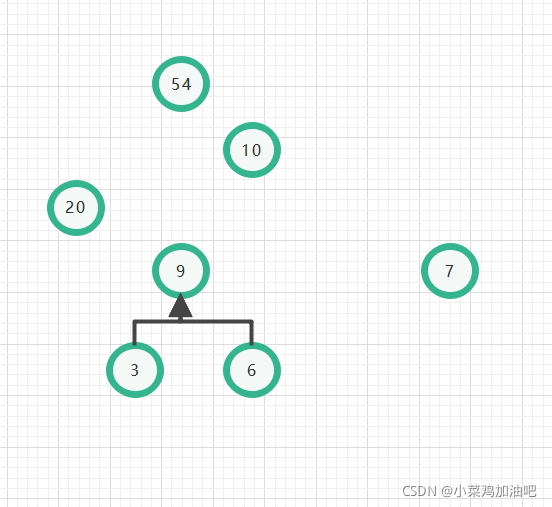
接下来一直重复一直重复~~

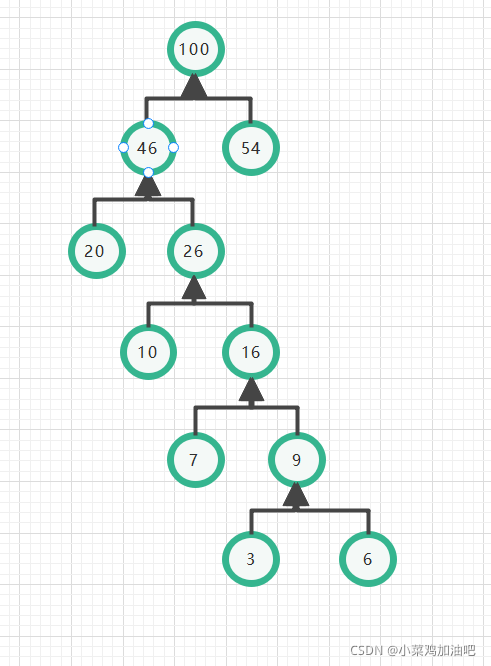
很显然~~~
你可以发现
它的每一个叶子都是衣服，而且，最大频率的里树根最近
这就形成了一棵哈夫曼树


接下来重点来了

哈夫曼编码

我们知道，编码方式有很多种常见的有ASCII编码，二进制编码等等
下面介绍一种哈夫曼编码
还是上面的衣服
我们规定：右子树为1，左子树为0（就是向右找就是1，向左找就是0）
可以根据图来分析一下

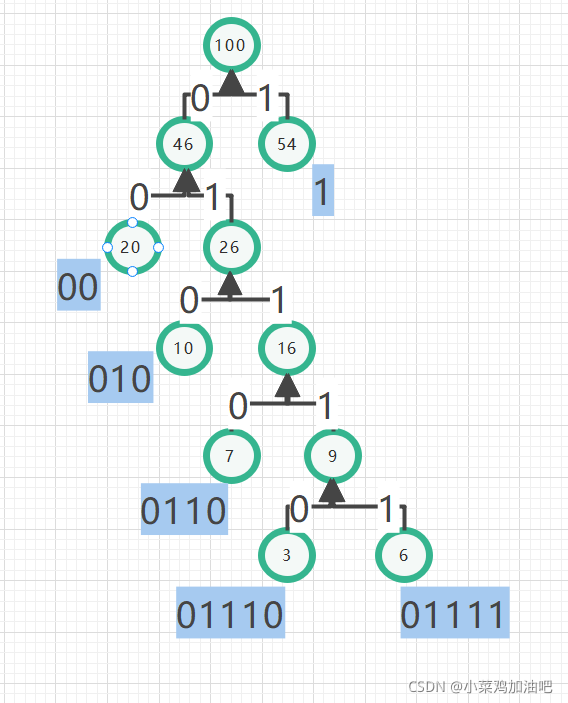
对于上面的衣服来说我们可以用ASCII编码也可以用2进制编码
当然也可以用哈夫曼编码
下面我们来分析一下哪一种效率最高（也就是用最短的码长实现编码）
$ASCII：8bit$
$二进制：3bit$
哈夫曼编码：因为哈夫曼编码的不定长性，我们要求出平均码长 ACL
$ACL=0.54\ast 1+0.20\ast 2+0.10\ast 3+0.07\ast 4+0.09\ast 5=1.97$

显然！！哈夫曼要小于另外两种编码长度

下面我们用代码实现上述哈夫曼树的构造

结合表格理解效果更佳~~~
这个表格也成为编译码表，可以说如果你用哈夫曼编码来给你朋友发信息，再厉害网警也绝对发现不了

结点	字符	概率	parent结点	left结点	right结点	code
1	A	54	11	0	0	1
2	B	10	9	0	0	010
3	C	6	7	0	0	01111
4	D	3	7	0	0	01110
5	E	7	8	0	0	0110
6	F	20	10	0	0	00
7		9	8	4	3
8		16	9	5	7
9		26	10	2	8
10		46	11	6	9
11		100		10	1

Huffman树节点结构

struct HTNode
{
	char ch;   //对应的字母，比如a
	int weight;//字母的出现次数，比如a出现了1000次
	int parent;
	int left;
	int right;
	char* code;
};

初始化树结构

void InitHTTable(int AsciiCount[], HTNode* &HT)
{
	for(int i = 0; i <= 128; i ++) AsciiCount[i] = 0;//将数组初始化为0
	
	AsciiCount[65] = 54;
	AsciiCount[66] = 10;
	AsciiCount[67] = 6;
	AsciiCount[68] = 3;
	AsciiCount[69] = 7;
	AsciiCount[70] = 20;
	
	HT=new HTNode[2 * 6];//生成动态空间[1...2n-1]
	int	CurrentASCII=0;//当前ASCII码
	HT[0].weight=0;
	for(int i = 1; i <= 6; i ++)
	{
		while(AsciiCount[CurrentASCII] == 0)//可能ASCII中有断档，找到计数不为零的那个字符
			CurrentASCII++;
			
		HT[i].ch = CurrentASCII;//j就是计数不为零的那个字符的ASCII码
		HT[i].weight = AsciiCount[CurrentASCII];//这是字符j的出现次数，作为哈夫曼的权重
		HT[i].parent = 0;//初始化双亲
		HT[i].left = 0;//初始化左孩子
		HT[i].right = 0;//初始化右孩子
		
		CurrentASCII++;//下一个ASCII码
	}
}

找最小的两个概率

void selectMin(HTNode* &HT,int end,int &min1,int &min2)
{//在数组HT[1...end]中，找两个权值最小的
	int i;
	min1 = 0;
	min2 = 0;
	for(i = 1; i <= end; i++)
	{
		if(HT[i].parent != 0)//如果这个结点已经有双亲了，说明他已经在树上了
			continue;
		else
		{
			if(min1 == 0)
				min1 = i;//记下最小值
			else if(HT[i].weight < HT[min1].weight)//找到更小的值
				min1 = i;			
		}
	}

	for(i = 1; i <= end; i++)
	{ 
		if(HT[i].parent != 0 || i == min1)
			continue;
		else
		{
			if(min2 == 0)
				min2 = i;
			else if(HT[i].weight < HT[min2].weight)
				min2 = i;			
		}
	}

	if(min1 > min2)
	{//保证min1是最小的
		int t = min1;
		min1 = min2;
		min2 = t;
	}

}

建树

void createHT(HTNode* &HT)
{//创建霍夫曼树，并得到霍夫曼编码
	int i = 0;
	for(i = 0; i <= 11; i++)
	{//初始化全部哈夫曼表格
		HT[i].parent=0;
		HT[i].left=0;
		HT[i].right=0;
	}

	for(i = 7; i <= 11; i++)
	{//形成哈夫曼树
		int min1, min2;
		selectMin(HT, i - 1, min1, min2);//从哈夫曼表前面i-1项中选择两个最小值，min1最小，构造出来的哈夫曼树左子树小
		HT[min1].parent = i;
		HT[min2].parent = i;
		HT[i].weight = HT[min1].weight + HT[min2].weight;//两个小概率合成一个结点
		HT[i].left = min1;
		HT[i].right = min2;
	}

	//生成叶子的哈夫曼节点
	int code_length = 0;

	for(i = 1; i <= 6; i++)
	{
		char code[128];//保存哈夫曼编码
		int j = i, k = 0;
		while(1)
		{
			int parentPosition = HT[j].parent;
			if(parentPosition == 0)
			{//这是根结点
				code[k] = '\0';
				HT[i].code = new char[k + 1];
				for(int x = 0; x < k; x++)
					HT[i].code[x] = code[k - 1 - x];
				HT[i].code[k] = '\0';
				
				printf("%c : %d : %s\n",HT[i].ch, HT[i].weight, HT[i].code);// 输出字符概率和编码值 
				break;
			}

			if(HT[parentPosition].left == j)
				code[k++] = '0';
			else
				code[k++] = '1';

			j = parentPosition;
		}
	}
}

完结撒花🌼🌻🌼🌻