POJ - 1159 Palindrome（最长公共子序列---空间压缩（滚动数组））

题目链接:https://cn.vjudge.net/contest/312755#problem/B

题意:给你一个数N，表示字符串的长度，接着一个字符串，找需要拼凑出回文串的最小增加个数。

思路:倒着把数组存一遍，找到两个字符串的最长公共子序列（LCS），字符串的长度减去LCS的长度，就是所求结果。

LCS解析:
$s_1{s}_2......s_n的子序列可以表示为S_{i1}{S}_{i2}......Sim（i1<i2<.....<im）--------->\ast \ast 子序列不一定是连续的\ast \ast$

$s=“abcd”;t=“becd”$
对应下表的各种情况（空白位置表示的是0）

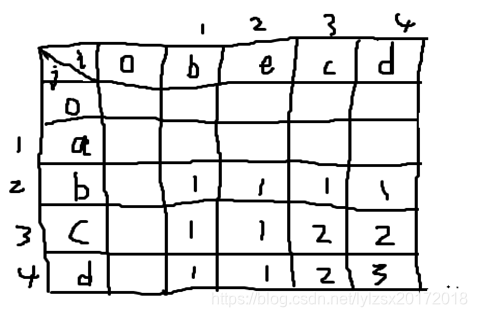
dp[i][j]:=s1…si和t1…tj对应的LCS的长度。
把上表赋予意义，就能得出递推关系式

$dp[i+1][j+1]=max(dp[i][j]+1,dp[i][j+1],dp[i+1][j])(S_{i+1}=t_{j+1}时)||max(dp[i][j+1],dp[i+1][j])(其他)$
此时的空间用了4*4的二维数组

优化:
dp就用两行表示状态，dp[2][N]

for(int i=0; i<N; i++){
        for(int j=0; j<N; j++){
            if(a[i]==b[j])
                dp[(i+1)%2][j+1]=dp[i%2][j]+1;
            else
                dp[(i+1)%2][j+1]=max(dp[i%2][j+1],dp[(i+1)%2][j]);
        }
    }

例如：
s=“Ab3bd”
t=“db3bA”

i=0时，(j=0~4)
$dp[1][1]=max(dp[0][1],dp[1][0])=0;$
$dp[1][2]=max(dp[0][2],dp[1][1])=0;$
$dp[1][3]=max(dp[0][3],dp[1][2])=0;$
$dp[1][4]=max(dp[0][4],dp[1][3])=0;$
$dp[1][5]=dp[0][4]+1=1;$$
i=2时，（j=0~4）
$dp[0][1]=max(dp[1][1],dp[0][0])=0 $
$//dp[1]时前一个状态，dp[1][1]表示s=A，t=d。$

$dp[0][2]=dp[1][2]+1=1;$

dp[0][3]=max(dp[1][3],dp[0][2])=1
//dp[1][3]表示前一个字母A遍历到j=2处，dp[0][2]表示字母b遍历到j-1处
dp[0][4]=max(dp[1][4],dp[0][3])=1;
dp[0][5]=max(dp[1][5],dp[0][4])=1;
i=3时，（j=0~4）
dp[1][1]=max(dp[1][0],dp[0][1])=0;
dp[1][2]=max(dp[1][1],dp[0][2])=1;//dp[1][2]更新为1,i=0时的dp[1][2]滚动到这里，并更新为1
dp[1][3]=dp[0][2]+1=2;//dp[1][3]更新为2
dp[1][4]=max(dp[1][3],dp[0][4])=1;//dp[1][4]更新为1
dp[1][5]=max(dp[1][4],dp[0][5])=1;//dp[1][5]更新为1

代码:

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int N,k;
char a[5020],b[5020];
int dp[5][5020];
int main(){
    scanf("%d",&N);
    k=0;
    memset(dp,0,sizeof(dp));
    scanf("%s",a);
    for(int i=N-1; i>=0; i--)
        b[k++]=a[i];
    for(int i=0; i<N; i++){
        for(int j=0; j<N; j++){
            if(a[i]==b[j])
                dp[(i+1)%2][j+1]=dp[i%2][j]+1;
            else
                dp[(i+1)%2][j+1]=max(dp[i%2][j+1],dp[(i+1)%2][j]);
        }
    }
    printf("%d\n",N-dp[N%2][N]);
    return 0;
}