算法总结归纳（一）

注：题目来源力扣https://leetcode-cn.com/

1、动态规划专题

        动态规划（英语：Dynamic programming， 简称 DP） 是一种在数学、 管理科学、 计算机科学、 经济学和生物信息学中使用的， 通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
        动态规划常常适用于有重叠子问题和最优子结构性质的问题， 动态规划方法所耗时间往往远少于朴素解法。

        动态规划背后的基本思想非常简单。 大致上， 若要解一个给定问题， 我们需要解其不同部分（即子问题） ， 再根据子问题的解以得出原问题的解。 动态规划往往用于优化递归问题， 例如斐波那契数列， 如果运用递归的方式来求解会重复计算很多相同的子问题， 利用动态规划的思想可以减少计算量。
        通常许多子问题非常相似， 为此动态规划法试图仅仅解决每个子问题一次， 具有天然剪枝的功能， 从而减少计算量： 一旦某个给定子问题的解已经算出， 则将其记忆化存储， 以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

1.1 岛屿的最大面积

        给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

eg.1
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。


eg.2
[[0,0,0,0,0,0,0,0]]
对于上面这个给定的矩阵, 返回 0。

思路分析： 使用深度优先搜索法，每当遇得未访问过的且为1的坐标，则dfs它的四个方向统计为1的个数并且标记已经访问过的坐标

class Solution {
public:
    vector<pair<int, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//上下左右四个方向
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int rowSize = grid.size(), colSize = grid[0].size(), maxRes = 0;
        vector<vector<bool>> visited(rowSize, vector<bool>(colSize, false));//visited[row][col]标记grid[row][col]是否访问过
        for (int row = 0; row < rowSize; ++row){
            for (int col = 0; col < colSize; ++col){
                //遇到坐标值为1，且没有访问过的点，统计这个岛屿的面积
                if (grid[row][col] && !visited[row][col]){
                    maxRes = max(maxRes, dfs(grid, visited, row, col));
                }
            }
        }
        return maxRes;
    }
    //统计grid[row][col]周围没有访问过的岛屿面积
    int dfs(vector<vector<int>>& grid, vector<vector<bool>> &visited, int row, int col){
        int rowSize = grid.size(), colSize = grid[0].size(), tempRes = 1;
        //出界、值为0，或者访问过
        if (row < 0 || row >= rowSize || col < 0 || col >= colSize || grid[row][col] == 0 || visited[row][col]){
            return 0;
        }
        visited[row][col] = true;//标记访问
        //四个方向递归，统计岛屿的面积
        for (auto &direction : directions){
            int nextRow = row + direction.first;
            int nextCol = col + direction.second;
            tempRes += dfs(grid, visited, nextRow, nextCol);
        }
        return tempRes;
    }
};

1.2 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

eg.1
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/ones-and-zeroes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

eg.2
输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

解题思路：本题是一个二维01背包dp问题。 物品就是strs里的字符串，背包容量就是题目描述中的m和n， 因此递推式为 dp[i][j] = max(dp[i][j], dp[i - one][j - zero] + 1)。 由于使用了二维滚动数组来降维，因此滚动数组外层循环从前往后，滚动数组内层循环从后往前。二维数组相当于每次刷新一遍。

动态规划：dp[n][m] n是1的个数，m是0个个数

状态转移：dp[i][j] = max(dp[i][j], dp[i - num_1][j - num_0]),num_1和num_0是一个字符串使用的1和0个数。

        本题通过三层循环，注意，最外层是字符串的循环，因为每个字符串只用一次，所以放在最外层，内层循环判断不同的dp[i][j]对该字符串能否构成，如果可以就加1。并且对不同的dp[i][j]当然要取最大值。

void count(string str, int &num_0, int &num_1){
	num_0 = 0, num_1 = 0;
	int len = str.size();
	for (int i = 0; i < len; i++){
		if (str[i] == '0') num_0++;
		else if (str[i] == '1')num_1++;
	}
}

int findMaxForm(vector<string>& strs, int m, int n) {
	int len=strs.size();
	vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
	int num_0, num_1;
	for (int k=0; k<len; k++){
		count(strs[k], num_0, num_1);
		for (int i=n; i>=num_1; i--){
			for (int j=m; j>=num_0; j--){
					dp[i][j] = max(dp[i][j], dp[i - num_1][j - num_0] + 1);
			}
		}
	}
	return dp[n][m];
}

1.3 矩阵区域和

给你一个 m * n 的矩阵 mat 和一个整数 K ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

 i - K <= r <= i + K, j - K <= c <= j + K
 (r, c) 在矩阵内。

eg.1
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]

eg.2
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], K = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

思路分析：
1.采用前缀和，先计算所有的横纵坐标的和。
   在分别计算每个坐标点和原坐标的关系，之后用前缀和相减

vector<vector<int>> matrixBlockSum(vector<vector<int>> mat, int k) {
	int a = mat.size();
	int b = mat[0].size();
	vector<vector<int>> arr(a + 1, vector<int>(b + 1));
	for (int i = 0; i < a; i++) {
		for (int j = 0; j < b; j++) {
			arr[i + 1][j + 1] = arr[i + 1][j] + arr[i][j + 1] - arr[i][j] + mat[i][j];
		}
	}
	vector<vector<int>> values(a, vector<int>(b));
	for (int i = 0; i < a; i++) {
		for (int j = 0; j < b; j++) {
			int s1 = i + 1 + k > a ? a : i + 1 + k;
			int s2 = j + 1 + k > b ? b : j + 1 + k;
			int e1 = i - k < 0 ? 0 : i - k;
			int e2 = j - k < 0 ? 0 : j - k;
			values[i][j] = arr[s1][s2] - arr[e1][s2] - arr[s1][e2] + arr[e1][e2];
		}
	}
	return values;
}

1.4 买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

dp[i][j] i表示第i天，j取0或者1，代表第i天卖出或持有股票

因此我们可以得到下面两个状态转移方程

dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])

int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2));
        dp[0][0] = 0, dp[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[n - 1][0];
    }

1.5 叶值的最小代价生成树

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

每个节点都有 0 个或是 2 个子节点。
数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

eg.
输入：arr = [6,2,4]
输出：32
解释：
有两种可能的树，第一种的非叶节点的总和为 36，第二种非叶节点的总和为 32。

    24            24
   /  \          /  \
  12   4        6    8
 /  \               / \
6    2             2   4

解题思路：我们发现数组中的数可以划分为两部分， 一半是左子树， 一半是右子树， 根节点就是左边最大和右边最大的乘积。 而左右子树里面的值就是当数组中的数为左子树的叶子节点时的情况， 右边一样。 直到数组中的数只有2个时， 答案就是左边右边相乘。
因此我们可以这么看， 如果2个数后面又加了一个数， 那么我们可以以01为一个节点再和2划分,也可以0 一个节点和12划分。
        树的左右两边至少有1个叶子结点。 如果有四个数， 有0 123, 01 23, 012 3,同时3个数又有之前的情况。因此我可以这样找状态， i代表起始点,j代表结束位置。 如果我想知道4个数的答案， 我就把上面划分的情况算出来， 每一个情况还要加上左边和右边的最大值的乘积， 作为根节点。 于是乎我就是要穷举所有状态。

int mctFromLeafValues(vector<int>& arr) {
    int size=arr.size();
    vector<vector<int>> dp(size,vector<int>(size,INT_MAX));
    vector<vector<int>> max(size,vector<int>(size,INT_MIN));
    for(int j=0;j<size;j++){
        dp[j][j]=0;
        int value=INT_MIN;
        for(int i=j;i>=0;i--){       
            value=std::max(value,arr[i]);
            max[i][j]=value;//arr[i:j]中最大值
        }
    }
    for(int len=1;len<size;len++){
        for(int i=0;i<size-len;i++){
            int j=i+len;
            for(int k=i;k<j;k++){
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+max[i][k]*max[k+1][j]);
            }
        }
    }
    return dp[0][size-1];
}

1.6 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

解题思路：

        由于路径的方向只能是向下或向右， 因此网格的第一行的每个元素只能从左上角元素开始向右移动到达， 网格的第一列的每个元素只能从左上角元素开始向下移动到达， 此时的路径是唯一的， 因此每个元素对应的最小路径和即为对应的路径上的数字总和。
        对于不在第一行和第一列的元素， 可以从其上方相邻元素向下移动一步到达， 或者从其左方相邻元素向右移动一步到达， 元素对应的最小路径和等于其上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。 由于每个元素对应的最小路径和与其相邻元素对应的最小路径和有关，因此可以使用动态规划求解。
        创建二维数组dp， 与原始网格的大小相同， dp[i][j] 表示从左上角出发到(i,j)(i,j) 位置的最小路径和。 显然， dp[0][0]=grid[0][0]。 对于dp中的其余元素， 通过以下状态转移方程计算元素值。
当i>0i>0 且j=0j=0 时， dp[i][0]=dp[i-1][0]+grid[i][0]。
当i=0i=0 且j>0j>0 时， dp[0][j]=dp[0][j-1]+grid[0][j]。
当 i>0i>0 且 j>0j>0 时， dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]。
最后得到dp[m-1][n-1]的值即为从网格左上角到网格右下角的最小路径和。

int minPathSum(vector<vector<int>>& grid) {

        if (grid.empty())
        {
            return 0;
        }

        int m = grid.size();
        int n = grid.at(0).size();

        vector<vector<int>> dp(m, vector<int>(n));
        dp.at(m - 1).at(n - 1) = grid.at(m - 1).at(n - 1); //右下角

        //最后一列
        for (int i = m - 2; i >= 0; --i)
        {
            dp.at(i).at(n - 1) = grid.at(i).at(n - 1) + dp.at(i + 1).at(n - 1);
        }

        //最后一行
        for (int j = n - 2; j >= 0; --j)
        {
            dp.at(m - 1).at(j) = grid.at(m - 1).at(j) + dp.at(m - 1).at(j + 1);
        }

        //从倒数第二行 第二列开始
        for (int i = m - 2; i >= 0; --i)
        {
            for (int j = n - 2; j >= 0; --j)
            {
                dp.at(i).at(j) = grid.at(i).at(j) + min(dp.at(i + 1).at(j), dp.at(i).at(j + 1));
            }
        }

        return dp.at(0).at(0);
    }

2、双指针专题

        双指针， 指的是在遍历对象的过程中， 不是普通的使用单个指针进行访问， 而是使用两个相同方向（快慢指针） 或者相反方向（对撞指针） 的指针进行扫描， 从而达到相应的目的。双指针法充分使用了数组有序这一特征， 从而在某些情况下能够简化一些运算。
 

2.1 盛最多水的容器     

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明： 你不能倾斜容器，且 n 的值至少为 2。

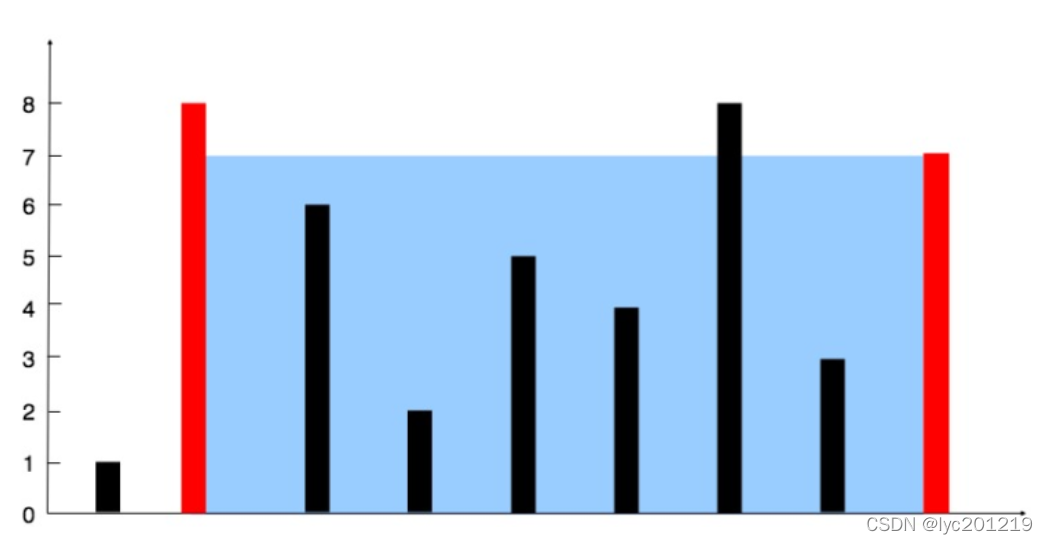
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）
的最大值为 49。
示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

         两线段之间形成的区域总是会受到其中较短那条长度的限制。我们使用两个指针，一个放在开始，一个置于末尾。 在每一步中，我们会计算指针所指向的两条线段形成的区域面积，并将指向较短线段的指针向较长线段那端移动一步。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;
        int right = height.size()-1;
        int maxarea = 0;
        while(left<right)
        {
            int now = min(height[left], height[right])*(right-left);
            maxarea = max(maxarea, now);
            if(height[left]<height[right])
                left++;
            else right--;
        }
        return maxarea;
    }
};

2.2 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例1：
输入：nums = [1,3,4,2,2]
输出：2

示例2：
输入：nums = [3,1,3,4,2]
输出：3

说明：

• 不能更改原数组（假设数组是只读的）。
• 只能使用额外的 O(1) 的空间。
• 时间复杂度小于 O(n2) 。
• 数组中只有一个重复的数字，但它可能不止重复出现一次。

解题思路：

题目中的要求：

• 不能更改原数组（假设数组是只读的），说明不能用排序的方法；
• 只能使用额外的 O(1) 的空间， 说明不能使用哈希表；
• 时间复杂度小于 O(n2)，说明不能用两层循环；

        可以使用二分查找的思想来做。首先介绍一下鸽巢原理：n+1 只鸽子放到 n 个鸽巢里，则肯定有一个鸽巢中的鸽子个数大于 1。则我们设置两个指针 left 和 right，计算 mid = (left+right)/2。统计输入数组 nums 中小于等于 mid 的元素个数 cnt，如果 cnt>mid，则说明 [left, mid] 之间的元素个数超过了 mid，则重复的数字一定在 [left, mid] 之间，否则重复的数字在 [mid+1, right] 之间。循环结束时，left 就是重复的元素。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int left = 1;
        int right = nums.size()-1;
        while(left<right){
            int mid = left+(right-left)/2;
            int cnt = 0;
            for(int num:nums){
                if(num<=mid) cnt++;
            }

            if(cnt>mid){
                right = mid; // 因为是循环条件是left<right，所以这里是 right=mid;
            }else{
                left = mid+1;
            }
        }
        return left;
    }
};

2.3 返回倒数第 k 个节点

        实现一种算法，找出单向链表中倒数第 k 个节点。返回该节点的值。

示例：

输入： 1->2->3->4->5 和 k = 2
输出： 4

解题思路：

        设置快和慢两个指针， 初始化时快指针比慢指针多走k-1步， 然后两个指针每次都走一步， 当快指针到达终点时， 慢指针正好处在倒数第k的位置。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */

class Solution {
public:
    int kthToLast(ListNode* head, int k) {
        ListNode *pre = head, *cur = head;
        for (int i = 0; i < k; i++)
            cur = cur->next;
        while (cur != nullptr) {
            pre = pre->next;
            cur = cur->next;
        }
        return pre->val;
    }
};

2.4 区间列表的交集

        给定两个由一些闭区间组成的列表，每个区间列表都是成对不相交的，并且已经排序。返回这两个区间列表的交集。

（形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b。两个闭区间的交集是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3]。）

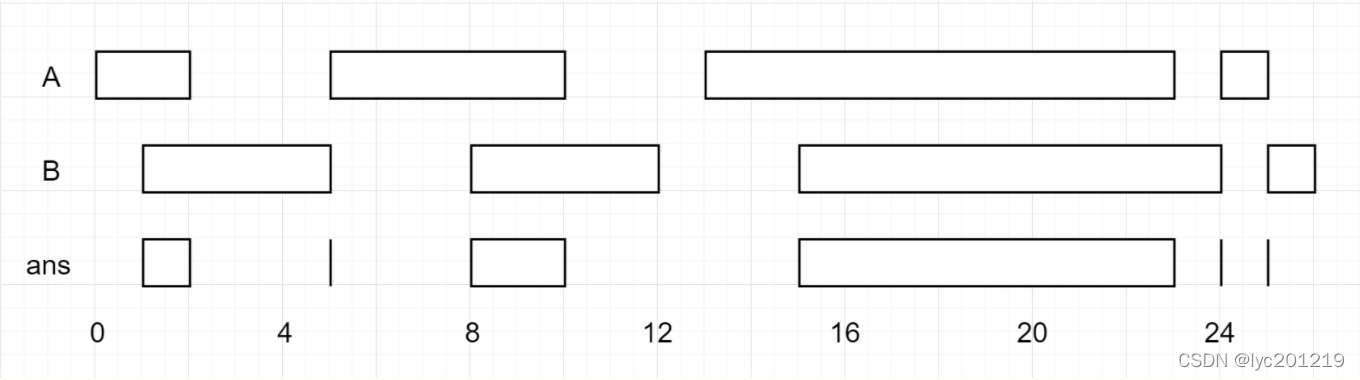
输入：A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
输出：[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
注意：输入和所需的输出都是区间对象组成的列表，而不是数组或列表。

解题思路：

1、给定的两个区间列表都是排好序的

2、用两个指针， 分别考察A、 B数组的子区间

3、根据子区间的左右边界， 求出一个交集区间

4、移动指针直至遍历完A、 B数组， 得到由交集区间组成的数

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        vector<vector<int>> result;
        if(firstList.size() == 0 || secondList.size() == 0)
            return result;
        int i = 0;
        int j = 0;
        while(i < firstList.size() && j < secondList.size())
        {
            int left = max(firstList[i][0], secondList[j][0]);          //子区间左边界
            int right = min(firstList[i][1], secondList[j][1]);         //子区间右边界
            if(left <= right)
                result.push_back({left, right});
            firstList[i][1] > secondList[j][1] ? j++ : i++;             //哪一个区间先结束，指针就先移动
        }
        return result;
    }
};

2.5 移除元素

        给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例1：
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例2：
输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

解题思路：

由于题目要求删除数组中等于等于val 的元素，因此输出数组的长度一定小于等于输入数组的长度，我们可以把输出的数组直接写在输入数组上。可以使用双指针：右指针right 指向当前将要处理的元素，左指针left 指向下一个将要赋值的位置。

如果右指针指向的元素不等于 val，它一定是输出数组的一个元素，我们就将右指针指向的元素复制到左指针位置，然后将左右指针同时右移；

如果右指针指向的元素等于val，它不能在输出数组里，此时左指针不动，右指针右移一位。

整个过程保持不变的性质是：区间 [0,left) 中的元素都不等于 val。当左右指针遍历完输入数组以后，left 的值就是输出数组的长度。

这样的算法在最坏情况下（输入数组中没有元素等于val），左右指针各遍历了数组一次。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int n = nums.size();
        int left = 0;
        for (int right = 0; right < n; right++) {
            if (nums[right] != val) {
                nums[left] = nums[right];
                left++;
            }
        }
        return left;
    }
};

3、二分查找专题

        二分查找也称折半查找（Binary Search） ， 它是一种效率较高的查找方法， 前提是数据结构必须先排好序， 可以在数据规模的对数时间复杂度内完成查找。 但是， 二分查找要求线性表具有有随机访问的特点 （例如数组） ， 也要求线性表能够根据中间元素的特点推测它两侧元素的性质， 以达到缩减问题规模的效果。

3.1 有序矩阵中第K小的元素

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

你必须找到一个内存复杂度优于 O(n2) 的解决方案。

示例1：
输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13


示例2：
输入：matrix = [[-5]], k = 1
输出：-5

解题思路：

矩阵的左上角为最小值，右下角为最大值，以最小值最大值为上下边界，求出中间值mid，遍历矩阵，统计到中间值mid有多少个数count，如果count小于k，说明第k小的数在mid后面，low = mid + 1，否则high = mid - 1。

class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int m = matrix.size(), n = matrix[0].size();
        int low = matrix[0][0];
        int high = matrix[m-1][n-1];

        while(low <= high){
            int mid = low + (high - low) / 2;
            int count = 0;

            for(int i = 0;i < m;++i){
                for(int j = 0;j < n && matrix[i][j] <= mid;++j){//统计到中间大的数据中有几个数
                    count++;
                }
            }
            if(count < k){//如果count < k，说明第k小的数在mid后面
                low = mid + 1;
            }
            else{
                high = mid - 1;
            }
        }
        return low;
    }
};

3.2 找出给定方程的正整数解

给你一个函数  f(x, y) 和一个目标结果 z，函数公式未知，请你计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。

尽管函数的具体式子未知，但它是单调递增函数，也就是说：

f(x, y) < f(x + 1, y)
f(x, y) < f(x, y + 1)
函数接口定义如下：

interface CustomFunction {
public:
  // Returns some positive integer f(x, y) for two positive integers x and y based on a formula.
  int f(int x, int y);
};

你的解决方案将按如下规则进行评判：

判题程序有一个由 CustomFunction 的 9 种实现组成的列表，以及一种为特定的 z 生成所有有效数对的答案的方法。
判题程序接受两个输入：function_id（决定使用哪种实现测试你的代码）以及目标结果 z 。
判题程序将会调用你实现的 findSolution 并将你的结果与答案进行比较。
如果你的结果与答案相符，那么解决方案将被视作正确答案，即 Accepted 。

示例1：
输入：function_id = 1, z = 5
输出：[[1,4],[2,3],[3,2],[4,1]]
解释：function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5：
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5


示例2：
输入：function_id = 2, z = 5
输出：[[1,5],[5,1]]
解释：function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5：
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5

解题思路：

1、x不变时， y增加f增加。 y不变时， x增加f增加。

2、x从1到1000时， 对y用二分， 确定f的值。

3、如果f(x,1) > z时， 不可能有合适的（x， y） 值， 算法结束。

4、如果f(x,1000) < z时， x到下一个值。

5、在f(x,1) <= z <= f(x,1000)时， 对y在(1,1000)中二分。

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        int x = 1;
        int y = z;

        for (int i = 1; i <= 1000; i++) {
            int l = 1;
            int r = 1000;

            while (l <= r) {
                int mid = l + (r - l) / 2;
                if (customfunction.f(i, mid) < z) {
                    l = mid + 1;
                } else if (customfunction.f(i, mid) > z){
                    r = mid - 1;
                } else {
                    ans.push_back({i, mid});
                    l = mid + 1;
                    r = mid - 1;
                }
            }
        }
        return ans;
    }
};

3.3 方阵中战斗力最弱的 K 行

给你一个大小为 m * n 的矩阵 mat，矩阵由若干军人和平民组成，分别用 1 和 0 表示。

请你返回矩阵中战斗力最弱的 k 行的索引，按从最弱到最强排序。

如果第 i 行的军人数量少于第 j 行，或者两行军人数量相同但 i 小于 j，那么我们认为第 i 行的战斗力比第 j 行弱。

军人 总是 排在一行中的靠前位置，也就是说 1 总是出现在 0 之前。

示例1：
输入：mat = 
[[1,1,0,0,0],
 [1,1,1,1,0],
 [1,0,0,0,0],
 [1,1,0,0,0],
 [1,1,1,1,1]], 
k = 3
输出：[2,0,3]
解释：
每行中的军人数目：
行 0 -> 2 
行 1 -> 4 
行 2 -> 1 
行 3 -> 2 
行 4 -> 5 
从最弱到最强对这些行排序后得到 [2,0,3,1,4]


示例2：
输入：mat = 
[[1,0,0,0],
 [1,1,1,1],
 [1,0,0,0],
 [1,0,0,0]], 
k = 2
输出：[0,2]
解释： 
每行中的军人数目：
行 0 -> 1 
行 1 -> 4 
行 2 -> 1 
行 3 -> 1 
从最弱到最强对这些行排序后得到 [0,2,3,1]

提示：

m == mat.length
n == mat[i].length
2 <= n, m <= 100
1 <= k <= m
matrix[i][j] 不是 0 就是 1

解题思路：

我们计算出方阵中每一行的战斗力（即每一行的元素之和） ， 再对它们进行排序即可。
 

class Solution {
public:
    vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {
        int len=mat.size();
        vector<pair<int,int>>v;
        for(int i=0;i<len;i++){
            int tmp=0;
            for(int n:mat[i]){
                if(n)tmp++;
                else break;
            }
            v.push_back(make_pair(tmp,i));
        }
        sort(v.begin(),v.end(),[](pair<int,int>a,pair<int,int>b){
            if(a.first==b.first)return a.second<b.second;
            else return a.first<b.first;
        });
        vector<int>ans;
        for(int i=0;i<k;i++)ans.push_back(v[i].second);
        return ans;
    }
};

3.4 两个数组的交集

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例1：
输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例2：
输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

解题思路：

如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。可以预见的是加入答案的数组的元素一定是递增的，为了保证加入元素的唯一性，我们需要额外记录变量pre 表示上一次加入答案数组的元素。

初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，且该数字不等于 pre ，将该数字添加到答案并更新pre 变量，同时将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size(), length2 = nums2.size();
        int index1 = 0, index2 = 0;
        vector<int> intersection;
        while (index1 < length1 && index2 < length2) {
            int num1 = nums1[index1], num2 = nums2[index2];
            if (num1 == num2) {
                // 保证加入元素的唯一性
                if (!intersection.size() || num1 != intersection.back()) {
                    intersection.push_back(num1);
                }
                index1++;
                index2++;
            } else if (num1 < num2) {
                index1++;
            } else {
                index2++;
            }
        }
        return intersection;
    }
};

3.5 寻找重复数

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例1：
输入：nums = [1,3,4,2,2]
输出：2

示例2：
输入：nums = [3,1,3,4,2]
输出：3

解题思路：

我们定义cnt[i] 表示 nums 数组中小于等于 i 的数有多少个，假设我们重复的数是 target，那么 [1,target−1]里的所有数满足 cnt[i]≤i，[target,n] 里的所有数满足 cnt[i]>i，具有单调性。

以示例 1 为例，我们列出每个数字的cnt 值：

示例中重复的整数是 22，我们可以看到[1,1] 中的数满足cnt[i]≤i，[2,4] 中的数满足 cnt[i]>i 。

如果知道 cnt[] 数组随数字 i 逐渐增大具有单调性（即target 前cnt[i]≤i，target 后cnt[i]>i），那么我们就可以直接利用二分查找来找到重复的数。

但这个性质一定是正确的吗？考虑nums 数组一共有 n+1 个位置，我们填入的数字都在 [1,n] 间，有且只有一个数重复放了两次以上。对于所有测试用例，考虑以下两种情况：

如果测试用例的数组中target 出现了两次，其余的数各出现了一次，这个时候肯定满足上文提及的性质，因为小于target 的数 i 满足 cnt[i]=i，大于等于 target 的数 j 满足 cnt[j]=j+1。

如果测试用例的数组中target 出现了三次及以上，那么必然有一些数不在 nums 数组中了，这个时候相当于我们用 target 去替换了这些数，我们考虑替换的时候对cnt[] 数组的影响。如果替换的数 i 小于 target ，那么 [i,target−1] 的 cnt 值均减一，其他不变，满足条件。如果替换的数 j大于等于 target，那么 [target,j−1] 的 cnt 值均加一，其他不变，亦满足条件。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size();
        int l = 1, r = n - 1, ans = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0; i < n; ++i) {
                cnt += nums[i] <= mid;
            }
            if (cnt <= mid) {
                l = mid + 1;
            } else {
                r = mid - 1;
                ans = mid;
            }
        }
        return ans;
    }
};

4、贪心算法专题 

        贪心算法（又称贪婪算法） 是指， 在对问题求解时， 总是做出在当前看来是最好的选择。 也就是说， 不从整体最优上加以考虑， 他所做出的是在某种意义上的局部最优解。
        贪心算法不是对所有问题都能得到整体最优解， 关键是贪心策略的选择， 选择的贪心策略必须具备无后效性， 即某个状态以前的过程不会影响以后的状态， 只与当前状态有关。

4.1 根据身高重建队列

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例1：
输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例2：
输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

解题思路：

按照 hi为第一关键字降序，ki为第二关键字升序进行排序。如果我们按照排完序后的顺序，依次将每个人放入队列中，那么当我们放入第 i个人时：

第 0,⋯,i−1 个人已经在队列中被安排了位置，他们只要站在第 i 个人的前面，就会对第 ii个人产生影响，因为他们都比第 i个人高；

而第 i+1,⋯,n−1 个人还没有被放入队列中，并且他们无论站在哪里，对第 i个人都没有任何影响，因为他们都比第 i个人矮。

在这种情况下，我们无从得知应该给后面的人安排多少个「空」位置，因此就不能沿用方法一。但我们可以发现，后面的人既然不会对第 i个人造成影响，我们可以采用「插空」的方法，依次给每一个人在当前的队列中选择一个插入的位置。也就是说，当我们放入第 i个人时，只需要将其插入队列中，使得他的前面恰好有 ki个人即可。

class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort(people.begin(), people.end(), [](const vector<int>& u, const vector<int>& v) {
            return u[0] > v[0] || (u[0] == v[0] && u[1] < v[1]);
        });
        vector<vector<int>> ans;
        for (const vector<int>& person: people) {
            ans.insert(ans.begin() + person[1], person);
        }
        return ans;
    }
};

4.2 避免重复字母的最小删除成本

        给你一个字符串 s 和一个整数数组 cost ，其中 cost[i] 是从 s 中删除字符 i 的代价。返回使字符串任意相邻两个字母不相同的最小删除成本。请注意，删除一个字符后，删除其他字符的成本不会改变。

示例 1：
输入：s = "abaac", cost = [1,2,3,4,5]
输出：3
解释：删除字母 "a" 的成本为 3，然后得到 "abac"（字符串中相邻两个字母不相同）。

示例 2：
输入：s = "abc", cost = [1,2,3]
输出：0
解释：无需删除任何字母，因为字符串中不存在相邻两个字母相同的情况。

示例 3：
输入：s = "aabaa", cost = [1,2,3,4,1]
输出：2
解释：删除第一个和最后一个字母，得到字符串 ("aba") 。

解题思路：

        每次遇到相邻的重复字母，就贪心的删除当前代价更小的那一个，也许后面还有和当前字符重复的字符而且代价更小，但因为只要是重复的字母都会被删除，所以当前这个字符最终也会因为有比他代价更高的相同字符而被删除掉，用这种贪心的做法可以得到最小的删除代价。

class Solution {
    public int minCost(String s, int[] cost) {
        int n = s.length();
        int res = 0;
        for(int i = 0; i < n - 1; i++) {
            int sum = cost[i], max = cost[i];
            while(i < n - 1 && s.charAt(i) == s.charAt(i+1)) {
                sum += cost[i+1];
                max = Math.max(max,cost[i+1]);
                i++;
            }
            res += sum - max;
        }
        return res;
    }
}

4.3 用户分组

有 n 个人被分成数量未知的组。每个人都被标记为一个从 0 到 n - 1 的唯一ID 。

给定一个整数数组 groupSizes ，其中 groupSizes[i] 是第 i 个人所在的组的大小。例如，如果 groupSizes[1] = 3 ，则第 1 个人必须位于大小为 3 的组中。

返回一个组列表，使每个人 i 都在一个大小为 groupSizes[i] 的组中。

每个人应该 恰好只 出现在 一个组 中，并且每个人必须在一个组中。如果有多个答案，返回其中 任何 一个。可以 保证 给定输入 至少有一个 有效的解。

示例：
输入：groupSizes = [3,3,3,3,3,1,3]
输出：[[5],[0,1,2],[3,4,6]]
解释：
第一组是 [5]，大小为 1，groupSizes[5] = 1。
第二组是 [0,1,2]，大小为 3，groupSizes[0] = groupSizes[1] = groupSizes[2] = 3。
第三组是 [3,4,6]，大小为 3，groupSizes[3] = groupSizes[4] = groupSizes[6] = 3。 
其他可能的解决方案有 [[2,1,6],[5],[0,4,3]] 和 [[5],[0,6,2],[4,3,1]]。


示例2：
输入：groupSizes = [2,1,3,3,3,2]
输出：[[1],[0,5],[2,3,4]]

解题思路：

        对于两个用户 x 和 y，如果 groupSize[x] != groupSize[y]，它们用户组的大小不同，那么它们一定不在同一个用户组中。因此我们可以首先对所有的用户进行一次【粗分组】，用一个哈希映射（HashMap）来存储所有的用户。哈希映射中键值对为 (gsize, users)，其中 gsize 表示用户组的大小，users 表示满足用户组大小为 gsize，即 groupSize[x] == gsize 的所有用户。这样以来，我们就把所有用户组大小相同的用户都暂时放在了同一个组中。

        在进行了【粗分组】后，我们可以将每个键值对 (gsize, users) 中的 users 进行【细分组】。由于题目保证了给出的数据至少存在一种方案，因此我们的【细分组】可以变得很简单：只要每次从 users 中取出 gsize 个用户，把它们放在一个组中就可以了。在进行完所有的【细分组】后，我们就得到了一种满足条件的分组方案。

class Solution {
public:
    vector<vector<int>> groupThePeople(vector<int>& groupSizes) {
        unordered_map<int, vector<int>> groups;
        for (int i = 0; i < groupSizes.size(); ++i) {
            groups[groupSizes[i]].push_back(i);
        }

        vector<vector<int>> ans;
        for (auto group = groups.begin(); group != groups.end(); ++group) {
            const int& gsize = group->first;
            vector<int>& users = group->second;
            for (auto iter = users.begin(); iter != users.end(); iter = next(iter, gsize)) {
                vector<int> dummy(iter, next(iter, gsize));
                ans.push_back(dummy);
            }
        }
        return ans;
    }
};

4.4 买卖股票的最佳时机 II

给定一个数组 prices ，其中 prices[i] 表示股票第 i 天的价格。

在每一天，你可能会决定购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以购买它，然后在 同一天 出售。
返回 你能获得的 最大 利润 。

示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 
这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候
卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出,
 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时
参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解题思路：

股票买卖策略：
        单独交易日： 设今天价格p1、 明天价格p2， 则今天买入、 明天卖出可赚取金额 p2-p1（负值代表亏损） 。
        连续上涨交易日： 设此上涨交易日股票价格分别为p1, p2,..., pn， 则第一天买最后一天卖收益最大，即pn-p1p； 等价于每天都买卖， 即 pn-p1=(p2-p1)+(p3-p2)+...+(pn-p{n-1})。
        连续下降交易日： 则不买卖收益最大， 即不会亏钱。
算法流程：
        遍历整个股票交易日价格列表 price， 策略是所有上涨交易日都买卖（赚到所有利润） ， 所有下降交易日都不买卖（永不亏钱） 。

        设tmp 为第 i-1 日买入与第i 日卖出赚取的利润， 即tmp = prices[i] - prices[i-1] ；
        当该天利润为正tmp > 0， 则将利润加入总利润 profit； 当利润为0或为负， 则直接跳过；
        遍历完成后， 返回总利润 profit。

class Solution {
public:
    int maxProfit(vector<int>& prices) {   
        int ans = 0;
        int n = prices.size();
        for (int i = 1; i < n; ++i) {
            ans += max(0, prices[i] - prices[i - 1]);
        }
        return ans;
    }
};

4.5 划分字母区间

        字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：

输入：S = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca", "defegde", "hijhklij"。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 的划分是错误的，因为划分的片段数较少。

解题思路：

        由于同一个字母只能出现在同一个片段，显然同一个字母的第一次出现的下标位置和最后一次出现的下标位置必须出现在同一个片段。因此需要遍历字符串，得到每个字母最后一次出现的下标位置。

        在得到每个字母最后一次出现的下标位置之后，可以使用贪心的方法将字符串划分为尽可能多的片段，具体做法如下。

       1、从左到右遍历字符串，遍历的同时维护当前片段的开始下标start 和结束下标 end，初始时 start=end=0。

        2、对于每个访问到的字母 c，得到当前字母的最后一次出现的下标位置 endc ，则当前片段的结束下标一定不会小于 endc，因此令end=max(end,endc)。

        3、当访问到下标end 时，当前片段访问结束，当前片段的下标范围是 [start,end]，长度为 end−start+1，将当前片段的长度添加到返回值，然后令 start=end+1，继续寻找下一个片段。

        4、重复上述过程，直到遍历完字符串。

上述做法使用贪心的思想寻找每个片段可能的最小结束下标，因此可以保证每个片段的长度一定是符合要求的最短长度，如果取更短的片段，则一定会出现同一个字母出现在多个片段中的情况。由于每次取的片段都是符合要求的最短的片段，因此得到的片段数也是最多的。

由于每个片段访问结束的标志是访问到下标 end，因此对于每个片段，可以保证当前片段中的每个字母都一定在当前片段中，不可能出现在其他片段，可以保证同一个字母只会出现在同一个片段。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int last[26];
        int length = s.size();
        for (int i = 0; i < length; i++) {
            last[s[i] - 'a'] = i;
        }
        vector<int> partition;
        int start = 0, end = 0;
        for (int i = 0; i < length; i++) {
            end = max(end, last[s[i] - 'a']);
            if (i == end) {
                partition.push_back(end - start + 1);
                start = end + 1;
            }
        }
        return partition;
    }
};