KMP原来是这样的

在网上已经有了很多关于KMP算法的视频和博客了，但是大部分讲解侧重于在KMP的理论原理和代码实现部分，
但是对代码的分析往往是一笔带过，并且我们的KMP算法非常的抽象。今天我们来和大家讲讲KMP到底是个啥？

问题引出

有一个字符串str1=“BBC ABCDAB ABCDABCDABDE”,和一个字符串str2=“ABCDABD”，现在要判断在str1中是否存在str2，假如存在则返回第一次出现的位置，假如不存在则返回-1。

在拿到这样的一道题时，首先我们脑海里的第一种思路往往是暴力模拟，就是让str1的每一个字符和str2匹配，假如不相同则后移到str1的下一个字符。但是这样往往会使我们进行很多重复且不必要的操作。所以有三位大佬研究出来KMP算法。

思路分析

不同于暴力模拟，KMP算法在str1中的字符与str2中的字符失配时，不再回溯到当前str1字符的下一个。

例如:
我们的ABCDABD在匹配BBC ABCDAB ABCDABCDABDE的时候，最后一个字符D与空格失配，那么我们不再从当前索引的移动一个字母到B开始匹配，而是直接移动4个字母到A匹配。

思考：那么我们这个向右移动的位数是怎么来的呢？

前缀后缀表

我们先来了解一下什么是前缀后缀表。例如在我们给定的“ABCDABD”中，我们可以来找每一节字符串的前缀后缀匹配值。

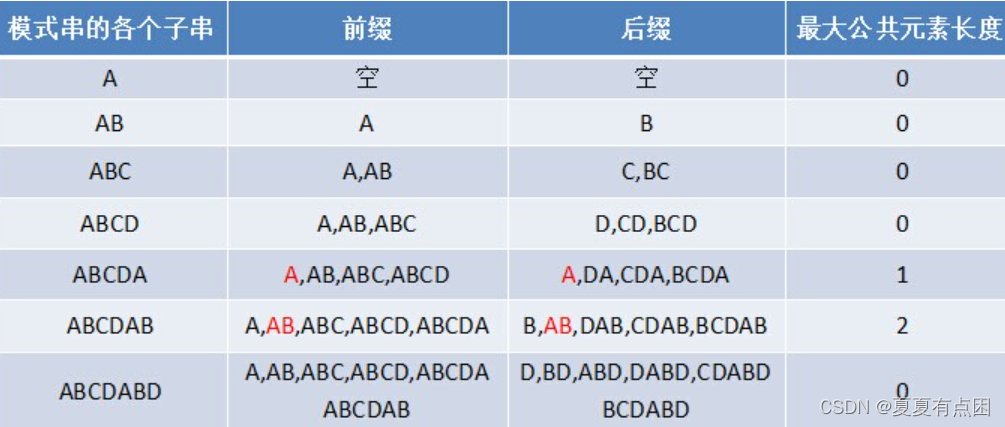
也就是说，我们可以得到下面的这张最大长度表：

从上面可以得到：

失配时，模式串向右移动的位数为：已匹配字符数 - 失配字符的上一位字符所对应的最大长度值

图解

因为模式串中的字符A跟文本串中的字符B、B、C、空格一开始就不匹配，所以不必考虑结论，直接将模式串不断的右移一位即可，直到模式串中的字符A跟文本串的第5个字符A匹配成功：

继续往后匹配，当模式串最后一个字符D跟文本串匹配时失配，显而易见，模式串需要向右移动。但向右移动多少位呢？因为此时已经匹配的字符数为6个（ABCDAB），然后根据《最大长度表》可得失配字符D的上一位字符B对应的长度值为2，所以根据之前的结论，可知需要向右移动6 - 2 = 4 位。

模式串向右移动4位后，发现C处再度失配，因为此时已经匹配了2个字符（AB），且上一位字符B对应的最大长度值为0，所以向右移动：2 - 0 =2 位。

A与空格失配，向右移动1 位。

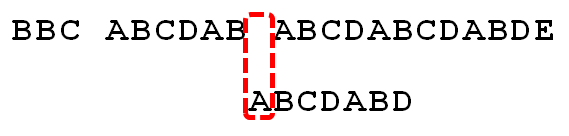
继续比较，发现D与C 失配，故向右移动的位数为：已匹配的字符数6减去上一位字符B对应的最大长度2，即向右移动6 - 2 = 4 位。

经历第5步后，发现匹配成功，过程结束。

package com.xxxx.tenmath;

public class KMP {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		String str1="BBC ABCDAB ABCDABCDABDE";
		String str2="ABCDABD";
		
		int[] next=kmpNext("ABCDABD");
		
		int index=kmpSearch(str1,str2,next);
		System.out.println("index="+index);
	}
	
	//写出我们的kmp搜索算法
	/**
	 * @param str1 原串
	 * @param str2 子串
	 * @param next 部分匹配表，是子串的
	 * @return 如果没有匹配到，返回-1；否则返回第一个匹配到的位置
	 */
	public static int kmpSearch(String str1,String str2,int[] next) {
		
		for(int i=0,j=0;i<str1.length();i++) {
			//需要处理str1.charAt(i)!=str2.charAt(j),去调整j的大小
			//kmp算法核心点
			while(j>0&&str1.charAt(i)!=str2.charAt(j)) {
				j=next[j-1];
			}
			
			
			if(str1.charAt(i)==str2.charAt(j)) {
				j++;
			}
			if(j==str2.length()) {
				return i-j+1;
			}
		}
		return -1;
	}
	
	//获取到一个字符串（子串）的部分匹配表
	public  static int[] kmpNext(String dest) {
		//创建一个next数组保存部分匹配值
		int[] next=new int[dest.length()];
		next[0]=0;//如果字符串的长度为1，部分匹配值就是0
		for(int i=1,j=0;i<dest.length();i++) {
			//当dest.charAt(i)!=dest.charAt(j),我们需要从next[j-1]获取新的j
			//直到我们发现有dest.charAt(i)==dest.charAt(j)成立才退出
			//这时kmp算法的核心点
			while(j>0&&dest.charAt(i)!=dest.charAt(j)) {
				j=next[j-1];
			}
			
			//当dest.charAt(i)==dest.charAt(j)满足时，部分匹配值就是+1
			if(dest.charAt(i)==dest.charAt(j)) {
				j++;
			}
			next[i]=j;
		}
		return next;
	}

}

本场最佳j=next[j-1]

在KMP中这句话让我困扰了两天，翻遍所有的视频讲解，几乎都是对这里一笔带过。哇咔咔，终于终于让我在一篇博客中找到了答案，给大家放上这篇博客的链接，他值得拥有姓名！！！
就是这篇博客