回溯法（暴力搜索）

原创已于 2022-03-06 15:15:43 修改 · 2.2k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #leetcode

于 2022-01-14 10:48:56 首次发布

数据结构与算法专栏收录该内容

8 篇文章

订阅专栏

1 回溯法概述

回溯法靠的是暴力穷举。

要理解的是，回溯是属于暴力搜索的一种。

回溯法是通过多叉树和递归实现的。也是一种树的深度优先遍历。

1.1 回溯法的中关于递归的探讨

第一：理解递归函数所能拿到的是什么：

进入一个递归函数，就代表拿到了一个选择列表！递归函数的目的就是在递归函数的内部，使用for循环遍历这个选择列表，实际上通常这个选择列表是传递给递归函数的。这个选择列表递归函数必须要知道。（另外，通常还要取得在这个列表的遍历的位置，这个通常设为startIndex）。
除此之外，递归函数还能拿到他自己的状态，这个状态最典型的就是Path。

第二：理解递归函数所拿到的状态：

可以说，除了选择列表之外，递归函数拿到的其他的属性都是他的状态。
递归函数状态的获取可以通过两种途径：一是从全局变量中（用全局变量记录所有递归函数的状态）；二是将状态以参数的形式传递给递归函数（类对象要以引用传递）。
以状态的代表path为例，进入一个递归函数，这个递归函数就有了一个path，往往这个path是设为全局的。可以在递归函数内部处理或者使用这个path。这个path实际上就是作为了一个递归函数的状态！
最重要的是，要理解，所谓的状态，不管是全局的还是作为参数传递给递归函数的，其实整个程序都是使用一个变量记录的！见下面的例子。

第三：理解base_case：
通常我们所说的base-case是递归的退出条件。实际上base_case理解为一个对本层递归状态进行判断的地方比较合适。如果满足我们所想要的状态条件，那么对本层递归的状态做出一种记录。只不过找到这种状态后，通常要加return语句返回而已。但是base_case的核心并不是return，而是对递归状态进行判断。

1.2 关于回溯法的模板

在这里插入图片描述
递归函数的退出有两种方法：

第一种是遍历的本层集合中的元素被遍历完了。就执行到递归函数的末尾自动结束。
第二种结束的方法是，在base_case中手动结束。这个base_case一般就是递归的退出条件。

2 组合问题

组合问题，要和子集问题对照着，其实他们两者本质上是一样的。！！求数组中的组合，就是求数组的子集啊！！

2.1 求给定数组的全部的组合

注意的几点：

1）首先是，关于递归的退出条件，也就是base_case，本题我们不需要手动设置base_case进行手动退出递归，因为本题递归到底层就行，所以使用递归函数遍历到底部会自动结束。
2）关于递归函数的选择列表和状态：若递归函数写成：void backing(vector< int >& nums,int startindex)，那么path状态就要写成全局的。递归函数的参数只有选择列表，选择列表是无论如何都在在递归函数参数中的。
3）关于递归函数的选择列表和状态：若递归函数写成：void backing(vector< int >& nums,int startindex，vector< int > path)，那么path状态就是使用参数传递给递归函数的。

下面是上述两种选择的cpp代码实现：

1）状态设置为全局：

class Sloluion2
{
    public:
    vector<int > path;//全局的

    void printall(vector<int> nums)
    {
        int n=nums.size();
        
        backing(nums,0);
    }
    
	//回溯的核心递归函数
    void backing(vector<int>& nums,int startindex)//参数里面只有必须的选择列表
    {
        //base_case
        //这里可以不写，因为这个base_case也正是下面循环的退出条件
        if(startindex>=nums.size())
            return ;

        for(int i=startindex;i<nums.size();i++)
        {
            //处理节点
            path.push_back(nums[i]);           
            for(int j=0;j<path.size();j++)
            {
                cout<<path[j]<<" ";
            }
            cout<<endl;


            backing(nums,i+1);
            path.pop_back();
        }
    }
};

int main()
{
	vector<int> nums={1,2,3,4};
	Slolution slu;
	slu.printall(nums);
	return 0;
}

2）状态作为参数传递给递归函数

class Sloluion2
{
    public:
    

    
    void printall(vector<int> nums)
    {
        int n=nums.size();
        vector<int > path;
        backing(nums,0,path);
    }
    void backing(vector<int>& nums,int startindex,vector<int>& path)//将path状态作为参数
    {
        //base_case
        //这里可以不写，因为这个ase_case也正是循环的推出条件
        if(startindex>=nums.size())
            return ;

        for(int i=startindex;i<nums.size();i++)
        {
            //处理节点
            path.push_back(nums[i]);           
            for(int j=0;j<path.size();j++)
            {
                cout<<path[j]<<" ";
            }
            cout<<endl;


            backing(nums,i+1,path);
            path.pop_back();
        }
    }
};

假设给定的nums={1,2,3,4},那么上述的代码的执行的流程如下图所示：

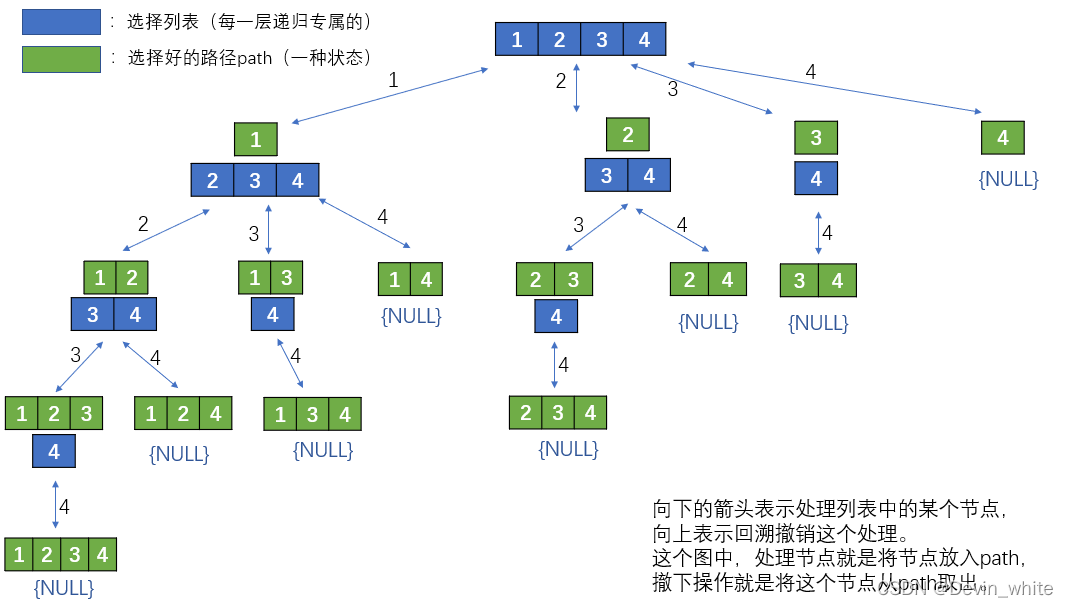
这个问题存在特殊性，就是一路递归到底，体现不出basae_case的实际作用。

2.2 T77组合问题

实际上，从上面的模板找那个额能看出的是，回溯法就是使用的多叉树的遍历遍历，但不能说是什么遍历顺序。他有着本身特有的遍历顺序。

这个题目就体现出base_case的作用了，因为不再是递归到底部了，而是满足一定的条件就停止。

下面还是给出两种方法，但是可以看出，状态设置为全局的代码会更加简洁，所以以后都将状态设置为全局的。

1）状态设为全局的

思路：
1、递归函数的设计

状态有path，还有给定的k。
所以递归函数的参数就只有选择列表。（本题的选择列表由n和startindex来控制）

2、base_case的设计
这个题目不能在递归到底了，要设计base_case。按照上面所总结的，base_case是一个对递归的状态进行判断的地方，这里我们进行状态的判断就是看看状态path中的元素数量是不是到了k。

//状态设置为全局的
//本题的状态有：path，以及path中的个数k。实际上k依赖于path
class Solution {
public:
    //全局的状态
    vector<vector<int>> res;
    vector<int> path;
    int count=0;
    
    vector<vector<int>> combine(int n, int k) 
    {
        count=k;
        backtracking(n,1);
        return res;
    }

    void backtracking(int n,int startindex)
    {
        if(path.size()==count)
        {
            res.push_back(path);
            return ;//也能算得上是剪枝，因为阻止了递归进行到底。不加这一行也是能AC的
        }    

        for(int i=startindex;i<=n;i++)
        {
            path.push_back(i);//处理节点
            backtracking(n,i+1);
            path.pop_back();//回溯，撤销处理的节点
        }
        
    }
};

2）状态以参数传递

//状态作为参数传递
class Solution2 {
public:
    vector<vector<int>> res;
    
    vector<vector<int>> combine(int n, int k) 
    {
        vector<int> path;
        backtracking(n,k,1,path);
        return res;
    }
    void backtracking(int n,int k,int startindex,vector<int>& path)//状态以参数传递
    {
        if(path.size()==k)
        {
            res.push_back(path);
            return ;
        }    

        for(int i=startindex;i<=n;i++)
        {
            path.push_back(i);//处理节点
            backtracking(n,k,i+1,path);
            path.pop_back();//回溯，撤销处理的节点
        }
        
    }
};

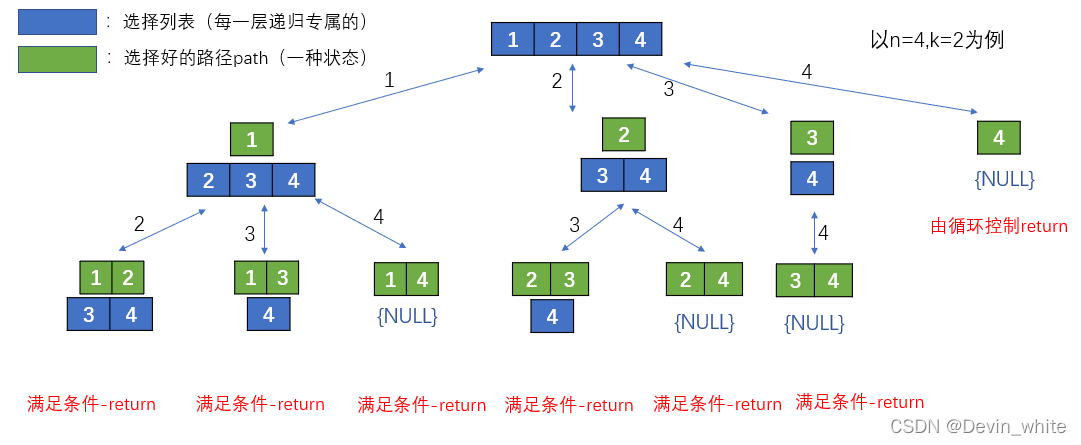
在这里插入图片描述

注意：

就像2.1所述一样，当我们的选择列表为NULL的时候，递归函数也会返回，也就是相当于执行完了递归函数中的for循环。
当满足我们base_case的时候，我们就是对path做一定的处理后主动的return结束递归！
也就是说，在递归函数backing的内部，有两个退出递归的机会，第一个就是for循环循环完毕，那么会自动的退出；第二个就是我们手动的退出。

3）剪枝操作
以后都使用“状态作为全局”，也就是上面的法一。这里也按照法一来进行剪枝优化。

关于剪枝：

剪枝操作就是将不必再进行的动作省去。要理解若不剪枝的话，递归就是进行到底的，是会遍历每一条路径，一直到最底层的。剪枝就是阻止某一层不必要的递归再往下进行。
剪枝一般有两个地方，一个是在for循环头处，也就是在选择列表处，一个是在base_case状态判断的时候。

当n=4,k=3的时候，需要进行的剪枝操作如下图所示，也就是说，什么时候需要进行剪枝呢，就是当选择列表中的元素已经不够我们的个数了，所以没必要再进行下去了。

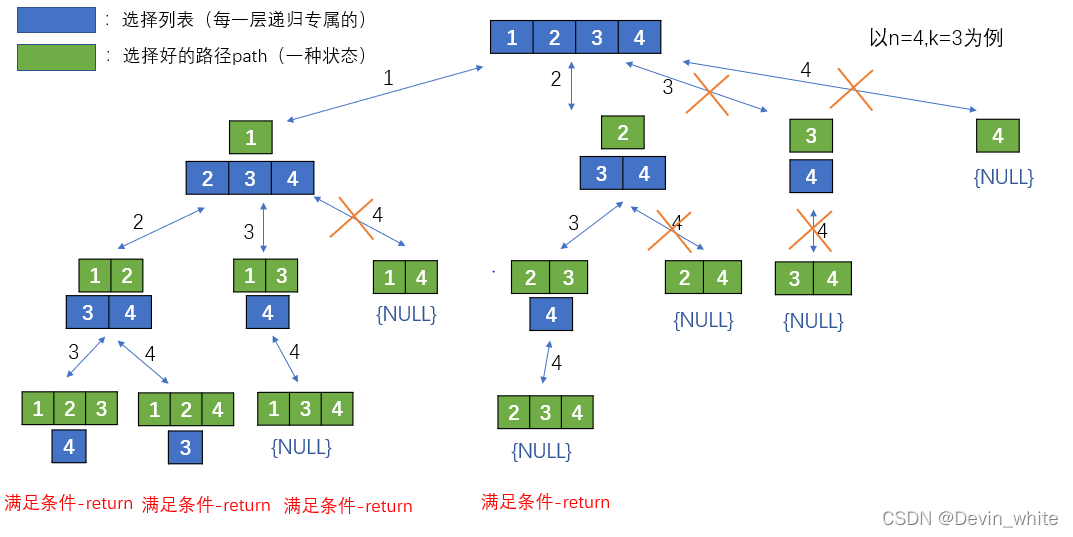
在这里插入图片描述
因为我们要控制我们已经选择的元素的个数，所以我们在选择列表进行选择的时候进行剪枝，也就是在for循环中。下面是进行了剪枝优化后的代码：

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    int count=0;
    vector<vector<int>> combine(int n, int k) 
    {
        count=k;
        backtracking(n,1);
        return res;
    }

    void backtracking(int n,int startindex)
    {
        if(path.size()==count)
        {
            res.push_back(path);
            return ;//也能算得上是剪枝，因为阻止了递归进行到底。不加这一行也是能AC的
        }    

        for(int i=startindex;i<=n - (count - path.size()) + 1;i++)//剪枝优化的地方
        {
            path.push_back(i);//处理节点
            backtracking(n,i+1);
            path.pop_back();//回溯，撤销处理的节点

        }
        
    }
};

2.3T216 组合总和III

通过这个题目，明白递归函数中的状态的传递和转移。状态的传递有两种方式：

第一种是在放在全局变量上，因为程序一定是执行到了某一个递归函数中，让全局变量代表这个进行到的递归函数的状态。
第二种是直接将递归函数的状态作为参数传入给递归函数。

分析：
1、设计递归函数
先分析每一递归所拥有的状态，本题来说有：path路径、path中的元素的和、path中的元素的个数、所要达到的目标元素和，这全都设置为全局的。因为选择列表已经得知（0~9），所以仅需startindex控制。

2、确定递归处理逻辑
也就是怎么更改本层的状态，一般来讲将本层递归遍历的节点放入path中，这是一定有的。另外，本题还要记录每层递归的path中元素的和。所以还要处理sum。将此级递归处理完后，还要进行状态的还原。

3、确定base_case
base_case的作用就是判断本层递归所持有的的状态，然后做出判断。如果满足就结束递归。

下面是cpp代码，一如既往，还是使用将状态作为全局变量的做法：

1）回溯法

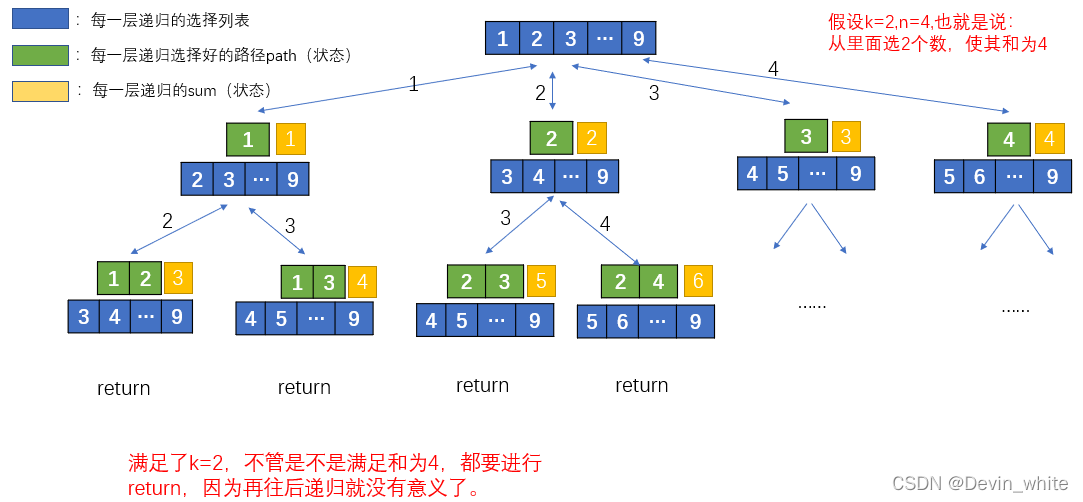
在这里插入图片描述

//状态设置为全局的
class Solution5 {
public:
    vector<int> path;//状态0，path
    vector<vector<int>> res; 
    int sum;//状态1：path里面的数据的总和
    int count;//状态2：path里面的元素的数量
    int targetsum;//状态3：要达到的目标的总和

    vector<vector<int>> combinationSum3(int k, int n) 
    {
        targetsum=n;
        count=k;
        backtracing(1);
        return res;
    }

    //从集合（1~9）中，选k个数，使其得到和为targetsum
    void backtracing(int startindex)
    {
        //base_case
        if(path.size()==count)
        {
            if(sum==targetsum)
            {
                res.push_back(path);
               return;
            }           
            return;//实际上也算是一个剪枝操作           
        }


        for(int i=startindex;i<=9;i++)
        {
            //更改自己的状态
            sum+=i;
            path.push_back(i);

            backtracing(i+1);

            //还原状态
            sum-=i;
            path.pop_back();            
        }
    }
};

2）回溯法的剪枝操作

要理解剪枝，首先要明白不剪枝的话是什么样的效果。不剪枝的话，递归是全部展开的，可以理解为base_case里面也没有return语句。实际上我们通常的操作就是找到满足条件的path后，就在base_case里进行return，这也算是一部分剪枝的操作。

本题其实有三个地方需要剪枝，第一个地方是，当递归的元素的个数已经大于等于k的时候，就不用继续进行下去了，这个剪枝操作已经在上面的法一中实现了。第二个是，某一层的递归的sum已经大于targetsum了，这也不用进行下去了。第三个地方是，当选择列表中所剩下的元素已经不够选择了。

上面所述的第三个剪枝操作和上一题是一样的。这里不再多说。第一个和第二个剪枝的操作是在base_case中实现的。之前也说过，base_case是一个对本层递归的状态进行判断的地方。，所以天然的是一个抑制往下递归的地方。

下面是剪枝之后的CPP代码：

class Solution5 {
public:
    vector<int> path;//状态0，path
    vector<vector<int>> res; 
    int sum;//状态1：path里面的数据的总和
    int count;//状态2：path里面的元素的数量
    int targetsum;//状态3：要达到的目标的总和


    vector<vector<int>> combinationSum3(int k, int n) 
    {
        targetsum=n;
        count=k;
        backtracing(1);
        return res;
    }

    //从集合（1~9）中，选k个数，使其得到和为targetsum
    void backtracing(int startindex)
    {
        //base_case--状态判断的地方
        if(sum>targetsum)//剪枝
            return;

        if(path.size()==count)
        {
            if(sum==targetsum)
            {
                res.push_back(path);
               return;//剪枝
            }           
            return;           
        }
        for(int i=startindex;i<=9-(count-path.size())+1;i++)//剪枝
        {
            //更改自己的状态
            sum+=i;
            path.push_back(i);

            backtracing(i+1);

            //还原状态
            sum-=i;
            path.pop_back();
            
        }
    }
};

2.3 T17电话号码的字母组合

通过这个题目理解循环和递归分别完成的任务是什么。

for循环是遍历当前查找的集合，递归完成的是查找下一个子集。

并且做题的时候要理清这两个东西分别是什么。

1、分析递归函数
递归函数的状态有：path。
每一层的选择列表由digits和startindex控制。

2、确定单层递归的逻辑
就是将遍历到的字符加入path

3、确定base_case

下面是CPP代码：

class Solution {
public:

    vector<string> res;
    string path;
    int n;

    vector<string> lettermap={
            "",
            "",
            "abc",
            "def",
            "ghi",
            "jkl",
            "mno",
            "pqrs",
            "tuv",
            "wxyz"
        };
    
    vector<string> letterCombinations(string digits) 
    {
        n=digits.size();
        if(n==0)
            return res;

        backtracking(digits,0);
        return res;
    }

    void backtracking(string &  digits,int startindex)
    {
        if(path.size()==n)
        {
            res.push_back(path);
            return ;
        }

        int digit=digits[startindex]-'0';
        string letters=lettermap[digit];

        for(int i=0;i<letters.size();i++)
        {
            path.push_back(letters[i]);

            backtracking(digits,startindex+1);

            path.pop_back();

        }
    }

};

2.4T39组合总和

通过这个题目，要明白的是，做题之前，一定要先用一个特例，画出树形结构，然后再写代码。画树形结构的时候也就是确定算法的过程。以这个题为例，若直接写代码，有些小条件可能会理不清。这个题目的元素可重复选取，但是结果的中不能有重复的组合就是很难确定的一个逻辑。必须要画出树状图才能看出来。
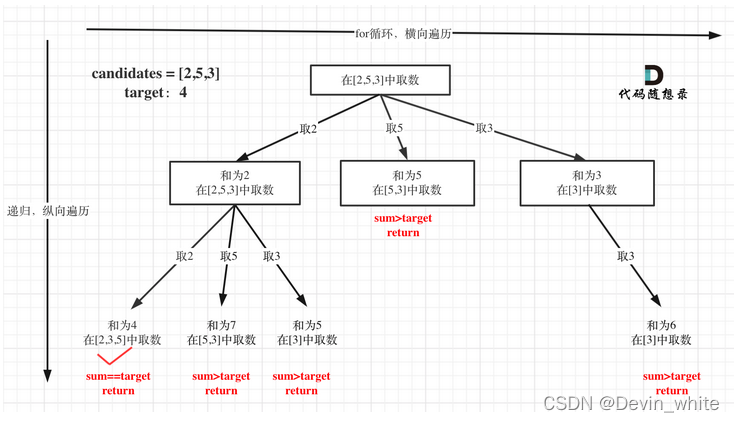
在这里插入图片描述

1、分析递归函数
递归的状态有path和sum，一如既往，将状态设为全局的。
选择列表是题目给定的数组，并且再加一个startindex一块控制选择列表。

2、确定递归处理逻辑
也就是怎么更改本层的状态，一般来讲将本层递归遍历的节点放入path中，这是一定有的。另外，本题还要记录每层递归的path中元素的和。所以还要处理sum。将次级递归处理完后，还要进行状态的还原！

3、确定base_case
base_case的作用就是判断本层递归所持有的的状态，然后做出判断。如果满足就结束递归。

4、确定遍历和递归的范围
就这个题目来讲，数组中的元素可以重复选取，但是结果中不能有重复的组合。因此将递归中的startindex不再每次都加1。但是for循环仍然是从startindex开始遍历

代码如下：

class Solution {
public:

    vector<int> path;
    vector<vector<int>> res;
    int sum;
    int targetsum;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
    {
        targetsum=target;
        sum=0;
        backtracing(candidates,0);
        return res;
    }

    void backtracing(vector<int> & nums,int startindex)
    {
        //base_case
        if(sum==targetsum)
        {
            res.push_back(path);
            return;//可以看做是剪枝（这一行也是抑制了无用的递归，去除这一行也是能通过的）
        }
        if(sum>targetsum)//剪枝
            return;


        for(int i=startindex;i<nums.size();i++)
        {
            //处理状态
            path.push_back(nums[i]);
            sum+=nums[i];

            backtracing(nums,i);//i不再加1

            //状态还原
            path.pop_back();
            sum-=nums[i];
        }
    }
};

2.5 T40 组合总和II

需要去重了，给定的数组中有重复元素，但是计算的结果不能有重复元素。

去重是在本层去重的。相同的元素可以在同一树枝中选取，但是不能在同一层中选取。

算法思路如下：
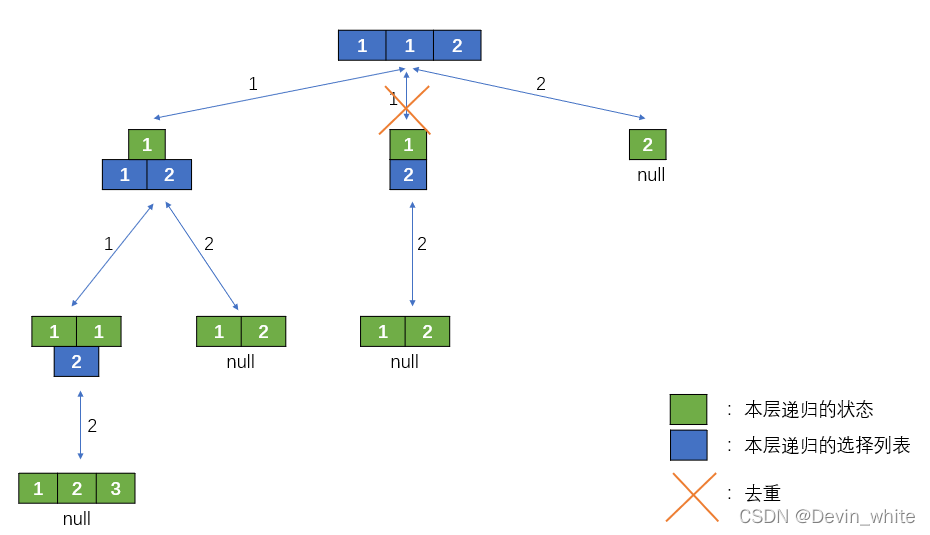
在这里插入图片描述
因为没有要求顺序，所以先进行排序后，直接在for循环体重就可以去重了。（如果不能排序的的话，就不能使用这个方法了见下面的题目）

同时注意下面代码的去重部分和剪枝部分。

class Solution {
public:
    vector<int> path;
    vector<vector<int>>res;
    int sum;
    int targetsum;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) 
    {
        sum=0;
        targetsum=target;
        sort(candidates.begin(),candidates.end());
        backtracing(candidates,0);
        return res;
    }

    void backtracing(vector<int>& nums,int startindex)
    {
        //base_case
        if(sum==targetsum)
        {
            res.push_back(path);
            return;//剪枝
        }

        if(sum>targetsum)//剪枝
            return;

        for(int i=startindex;i<nums.size();i++)
        {
            if(i>startindex && nums[i]==nums[i-1])//去重
                continue;
            path.push_back(nums[i]);
            sum+=nums[i];

            backtracing(nums,i+1);

            path.pop_back();
            sum-=nums[i];
            
        }
    }
};

3 切割问题

切割问题的思路和组合问题是类似的。
不同的是：切割问题在for循环中切割的时候，得到的不再是一个数字，而是从startindex到i的一个字符串。！

3.1 T131分割回文串

思路如下：
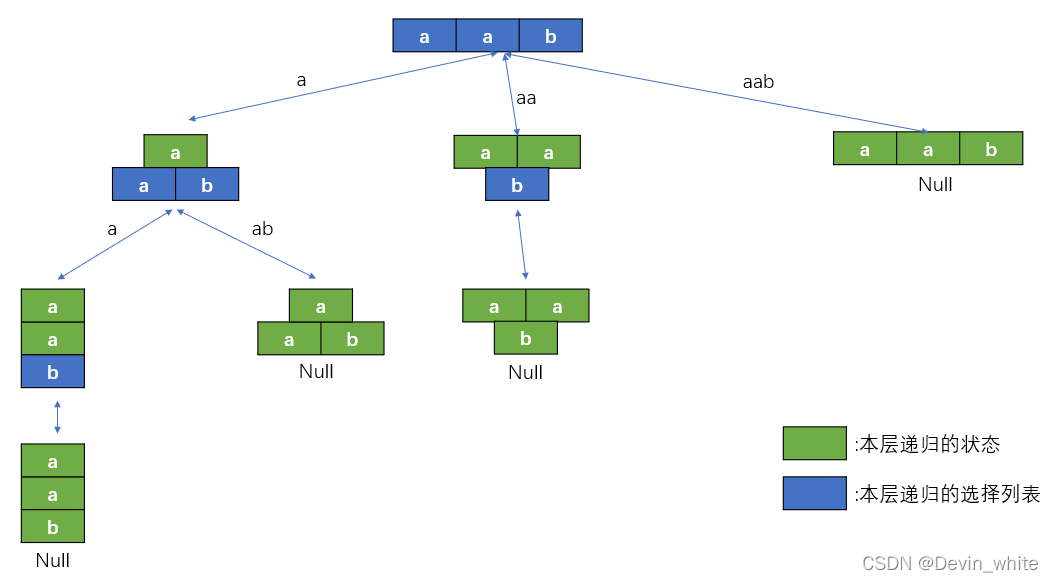
在这里插入图片描述
1、确定递归状态和选择列表
递归的状态还是只有path，只不过这里的path需要是一个 vector< string > 。
选择列表由题目给出，并添加一个startindex一起控制。

2、确定单层的递归逻辑
单层递归逻辑就是在for循环中切割，并将其添加到path中

3、确定base_case
这个题目递归到末尾就行了，并且要在递归的末尾处进行状态判断，如果当前path中的所有string都是回文串，那么将其添加到res中。但是这个题目可以使用剪枝优化，当新添加到path中的string不是回文串，那么则一层递归往后就没必要进行了。因为path中只要有一个不是回文串，那么这个path就肯定不符合条件！

4、确定for的开始和startindex的确定
常规

1）未优化版–直接在递归结束的时候，挨个判断path中的string

下面是cpp代码：

class Sloluion
{
    public:
    vector<string> path;
    vector<vector<string>> res;
        void backtracking(string& str,int startindex)//startindex表示从其尾后切割
        {
            if(startindex==str.size())//递归到末尾
            {
                for(int i=0;i<path.size();i++)
                {
                    if(!ispla(path[i]))
                    {
                        return;
                    }
                }
                res.push_back(path);
            }

            for(int i=startindex;i<str.size();i++)
            {
                path.push_back(str.substr(startindex,i-startindex+1));

                backtracking(str,i+1);

                path.pop_back();
            }
        }

        bool ispla(string & str)
        {
            int n=str.size();
            int right=n-1;
            int left=0;
            while(right>=left)
            {
                if(str[left]==str[right])
                {
                    left++;
                    right--;
                }
                else
                    return false;
            }
            return true;
        }
    vector<vector<string>> partition(string s) 
    {
        backtracking(s,0);
        return res;
    }
};

2）优化版–将新添加到path中的string进行判断
如果新添加到进去的不是回文串，那么就没必要再递归下去了，直接return即可。
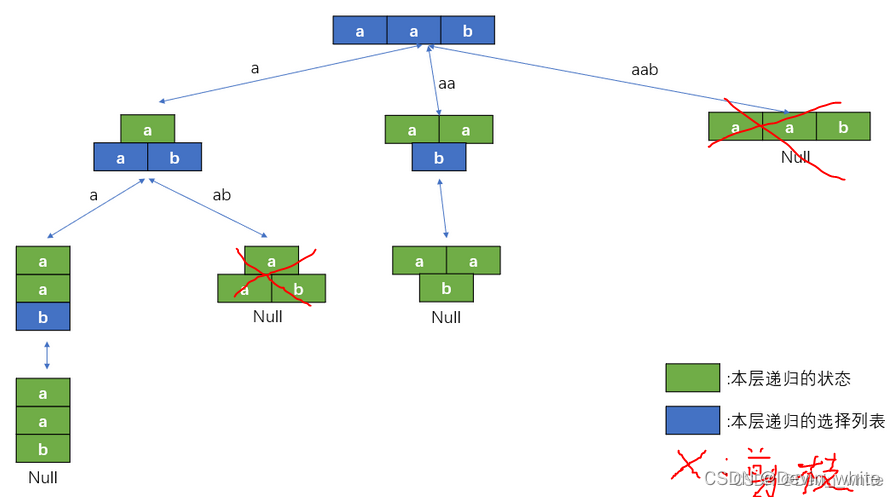
在这里插入图片描述
（上面的例子过于特殊，剪枝的点正好是递归的结束，但不代表剪枝没有意义）

class Solution
{
    public:
    vector<string> path;
    vector<vector<string>> res;
        void backtracking(string& str,int startindex)//startindex表示从其尾后切割
        {
            if(path.size()>0 && !ispla(path.back()))//剪枝
                return;
            
            if(startindex== str.size())//进行到递归末尾在pushback
                res.push_back(path);
            

            for(int i=startindex;i<str.size();i++)
            {
                path.push_back(str.substr(startindex,i-startindex+1));

                backtracking(str,i+1);

                path.pop_back();
            }
        }

        bool ispla(string & str)
        {
            int n=str.size();
            int right=n-1;
            int left=0;
            while(right>=left)
            {
                if(str[left]==str[right])
                {
                    left++;
                    right--;
                }
                else
                    return false;
            }
            return true;
        }
    vector<vector<string>> partition(string s) 
    {
        backtracking(s,0);
        return res;
    }
};

3.2 T93复原IP地址

这个题与上面的思路相同。

还是以前的套路：
在base_case中进行本层递归的状态的判断。
在for循环中对针对遍历到的位置进行递归状态的改变与还原。

1、确定递归的状态和选择列表
递归的状态还是只有path
选择列表是题目给的，再加一个startindex加以控制。

2、确定单层递归逻辑
还是在for循环中针对遍历到的位置进行本层递归状态的修改与撤销。

3、base_case的确定
base_case还是一个来对本层的递归的状态进行判断与选择的地方。

下面是CPP代码：

class Solution {
public:
    vector<string> path;
    vector<string> res;
    vector<string> restoreIpAddresses(string s) 
    {
        //提前排除错误的输入
        if(s.size()>12)
            return res;
        for(char c :s)
        {
            if(c>'9' || c<'0')
                return res;
        }

        backtrcking(s,0);
        return res;
    }
    void backtrcking(string & s,int startindex)
    {
       //base_case-递归状态的判断
       //这里通过path.back()来判断新加入path中的元素是不是一定的条件。（不用在循环里判断，统一在base-case中判断即可）
       //base_case就是判断递归状态的地方。
        if(path.size()>4)//剪枝
            return;
        if( path.size()!=0 && path.back().size()>1 && path.back()[0]=='0')//剪枝
            return;
        if(path.size()!=0 && stol(path.back())>255)//剪枝
            return;
        

        if(startindex==s.size())//进行到递归的尽头再结束
        {
            if(path.size()==4)
            {
                res.push_back(changeip(path));
                
            }
            return;//可以不加，由下面循环控制退出
        }


       for(int i=startindex;i<s.size();i++)
       {
           path.push_back(s.substr(startindex,i-startindex+1));//从startindex的末尾进行切割

           backtrcking(s,i+1);

           path.pop_back();
       } 
    }

    string changeip(vector<string> & path)
    {
        string temp=path[0]+'.'+path[1]+'.'+path[2]+'.'+path[3];
        return temp;
    }

};

4 子集问题

4.1 T78子集

不管是什么题目，首先，将算法通过树形他展示出来。
理论上说，只要树状图能按一定的逻辑画出来，就找到了解决的算法。用代码复现出来即可。

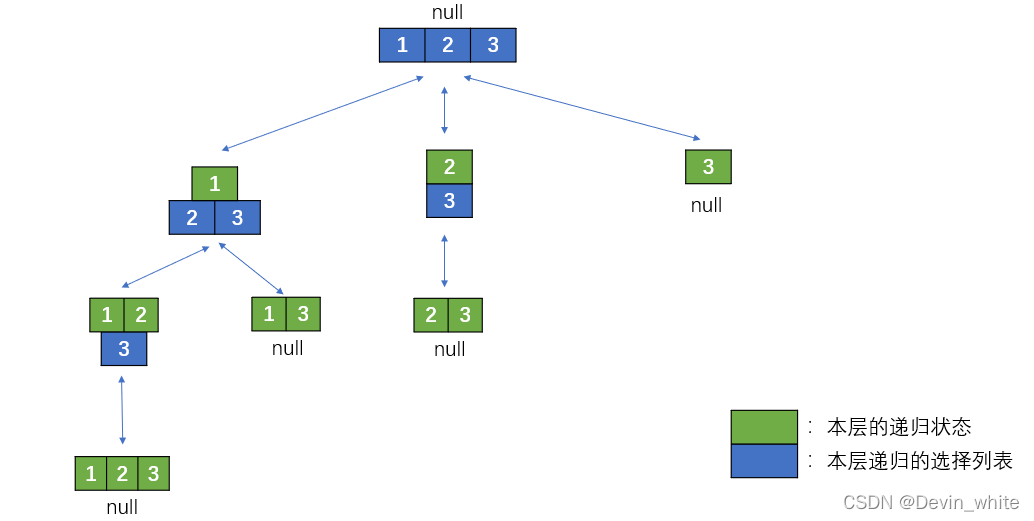
在这里插入图片描述

递归的状态还是只有path，从图中可以看出，我们要的答案就是每一次递归的状态的集合。

所以在base_case中进行将本层的path加入res即可：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        backtracing(nums,0);
        return res;
    }
    void backtracing(vector<int> & nums ,int startindex)
    {
        //base_case
        res.push_back(path);

        if(startindex=nums.size())//完全可以不加这个，因为这就是下面循环的自动退出条件
        {
            return;
        }


        for(int i=startindex;i<nums.size();i++)
        {
            path.push_back(nums[i]);

            backtracing(nums,i+1);

            path.pop_back();
        }
    }
};

4.2 T90子集II

这个问题的难处就是如何解决重复与不重复的问题。也就是如何在含有重复元素的数组中找出符合规定的不重复的数组。
关键还是如何正确画出树状图？
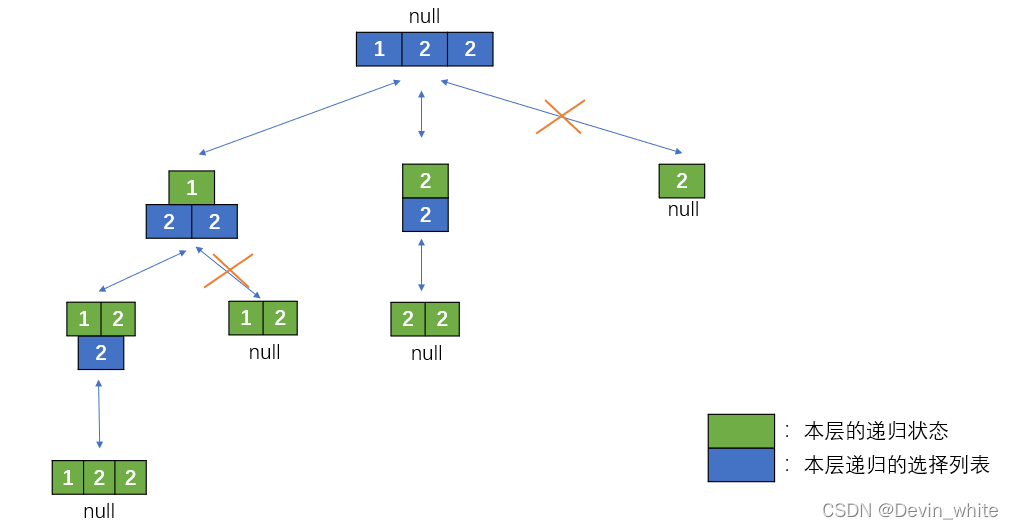
在这里插入图片描述

画出了上面的树形图，解决的算法就有了。注意去重是在对选择列表进行遍历的时候，也就是在for循环的时候。

(注意，这里可以通过直接在for中去重是因为，我们已经sort过nums数组了！所以重复的元素必然连续！)

代码如下：

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    vector<vector<int>> subsetsWithDup(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end());
        backtracing(nums,0);
        return res;
    }
    void backtracing(vector<int> &nums,int startindex)
    {
        //base_case
        res.push_back(path);

        if(startindex==nums.size())//可以不加，因为则就是下面循环的推出条件
            return;

        for(int i=startindex;i<nums.size();i++)
        {
            //去重
            if(i>startindex && nums[i]==nums[i-1])
                continue;
            
            path.push_back(nums[i]);
            
            backtracing(nums,i+1);

            path.pop_back();
        }


    }
};

4.3 递增子序列

法1）找出所有的序列（去重后的），然后在base_case中进行状态判断（判断是不是递增的）
思路如下图：
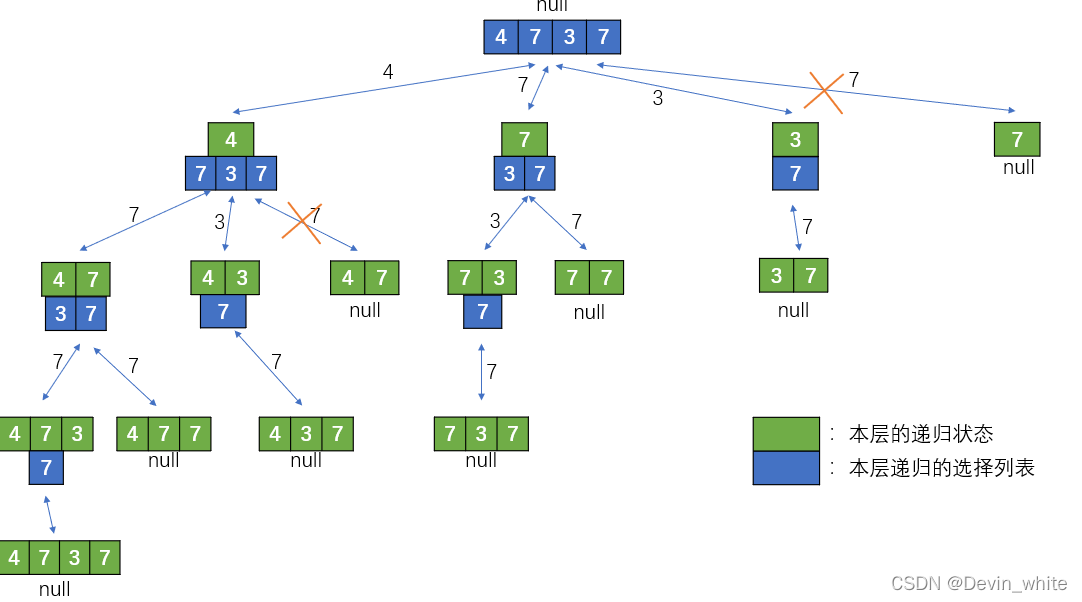
在这里插入图片描述
这是常规想到的，按照前面所说的，去重是在for循环中进行的。但是这里和上个题目不一样，因为这个题目无法sort，所以重复的元素不是相邻的。所以要想另一种办法。这里使用一个辅助数组。（去重使用set是最直观想到的，但是这个元素值在正负100之间，所以使用数组性能会更好）

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    
    vector<vector<int>> findSubsequences(vector<int>& nums) 
    {
        backtracing(nums,0);
        return res;
    }
    void backtracing(vector<int> & nums,int startindex)
    {
        //base_case--递归的状态的判断
        if(path.size()>1&& isbigger(path) )
            res.push_back(path);
        if(startindex==nums.size())//表示递归到底，也可以不加
            return ;
        //base-case状态判断结束

        int used[201]={0};//unordered_set<int>set;
        for(int i=startindex;i<nums.size();i++)
        {
            if(used[nums[i]+100]==0)//if(set.find(nums[i])==set.end())
            {
                path.push_back(nums[i]);
                used[nums[i]+100]=1;//set.inset(nums[i]);
            }
            else   
                continue;

            backtracing(nums,i+1);

            path.pop_back();
        }
    }
    bool isbigger(vector<int> & nums)
    {
        
        for(int i=1;i<nums.size();i++)
        {
            if(nums[i]<nums[i-1])
                return false;
        }
        return true;
    }
};

2）另一种对递归状态进行判断的方式—（剪枝）
所谓的递归的状态，本题中仅仅是path而已，状态的判断，就是对path是不是升序进行判断，如果path不是升序的，直接return结束递归就可以了。而上面法一是直接递归到底的，没有进行剪枝。

本题剪枝的位置是base_case中进行状态判断的时候，实际上这层不符合条件的递归已经开始了。所以注意下图中的进行剪枝的位置。（区别于在for循环中进行的剪枝。）
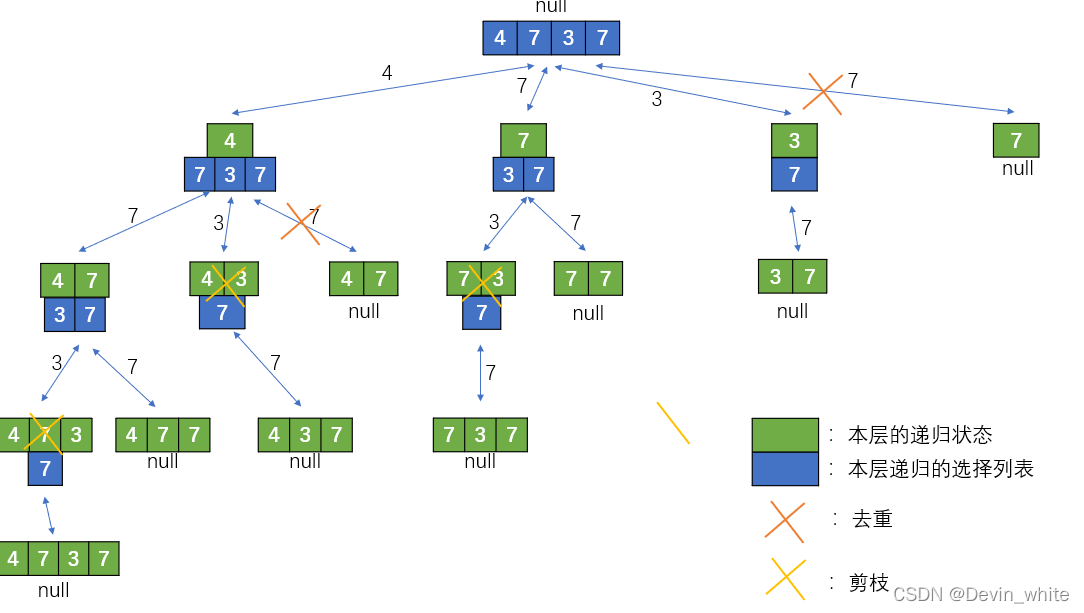
在这里插入图片描述

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;

    
    vector<vector<int>> findSubsequences(vector<int>& nums) 
    {
        backtracing(nums,0);
        return res;
    }
    void backtracing(vector<int> & nums,int startindex)
    {
        //base_case--递归的状态的判断
        
        /*直接这样写，比下面的更简单，而且更具通用性！！！！
        		if(path.size()>1 && path[path.size()-1]<path[path.size()-2])
            return;
				*/
        if(path.size()>1 && !isbigger(path))
            return;

        if(path.size()>1)
            res.push_back(path);
        if(startindex==nums.size())//表示递归到底，也可以不加
            return ;
        //base-case状态判断结束

        int used[201]={0};//unordered_set<int>set;
        for(int i=startindex;i<nums.size();i++)
        {
            if(used[nums[i]+100]==0)//if(set.find(nums[i])==set.end())
            {
                path.push_back(nums[i]);
                used[nums[i]+100]=1;//set.inset(nums[i]);
            }
            else   
                continue;

            backtracing(nums,i+1);

            path.pop_back();
        }
    }
    bool isbigger(vector<int> & nums)
    {
        
        for(int i=1;i<nums.size();i++)
        {
            if(nums[i]<nums[i-1])
                return false;
        }
        return true;
    }
};

5 排列问题

5.1 T46全排列

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。也就是说，每次都把相同的选择列表传递给每一层递归函数。

但是因为每一个元素只能使用一次，因此需要另一个状态变量来记录这层递归中，已经使用过和未使用过的选择列表中的元素。

算法流程如下：
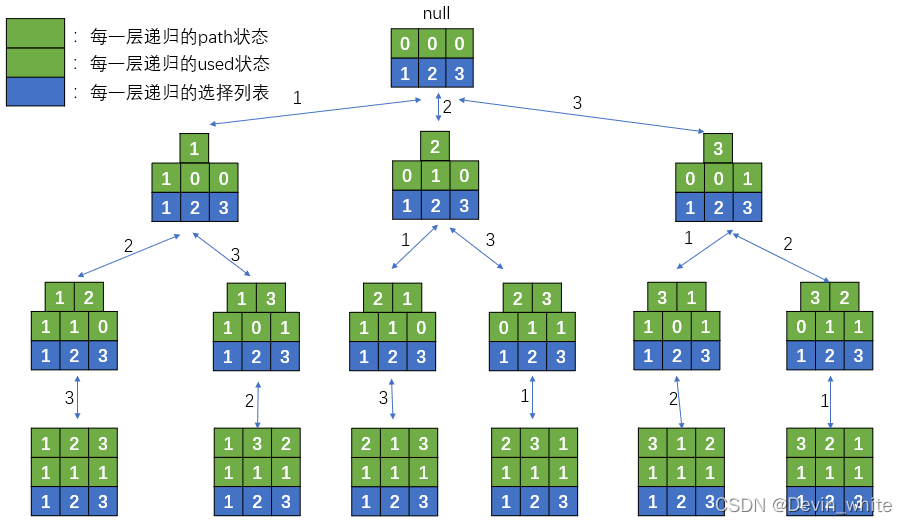
在这里插入图片描述

1、确定递归函数
首先是递归的状态，除了必须要有的path外，还需要一个状态来记录每一层递归的选择列表中的可以使用的元素。

选择列表：不再需要startindex来控制了。

2、确定单层递归逻辑
还是使用for来循环选择列表，并使用本层的used进行控制循环的元素选择。
for中，要完成递归状态的改变和还原

3、确定base_case
base-case中进行状态的判断，当path符合退出条件的时候，就添加到res中。

下面是cpp代码：

class Solution {
public:

    vector<int> path;
    vector<vector<int>> res;
    vector<int> used;
    vector<vector<int>> permute(vector<int>& nums) 
    {
        used.assign(nums.size(),0);
        backtracing(nums);
        return res;
    }

    void backtracing(vector<int> & nums)
    {
        //base_case
        if(path.size()==nums.size())
        {
            res.push_back(path);
            return;//也可以不加这个，由下面的循环控制退出
        }

        for(int i=0;i<nums.size();i++)
        {
            if(used[i]==0)
            {
                path.push_back(nums[i]);
                used[i]=1;
            }
            else
                continue;

            backtracing(nums);

            path.pop_back();
            used[i]=0;
        }

    }
};

5.2 T47全排列II

这个问题在上一个题目的基础上进行去重就行了。
之前提到过，去重是在for循环中进行的。

但是全排列的去重和之前的去重也有点区别。因为全排列问题的选择列表是题目给定的完整的列表，当执行nums[i-1]==nums[i]的时候，nums[i-1]不一定是被使用了。结合下面的代码理解：
在这里插入图片描述

class Solution {
public:

    vector<int> path;
    vector<vector<int>> res;
    vector<int> used;
    vector<vector<int>>  permuteUnique(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end());
        used.assign(nums.size(),0);
        backtracing(nums);
        return res;
    }

    void backtracing(vector<int> & nums)
    {
        //base_case
        if(path.size()==nums.size())
        {
            res.push_back(path);
            return;//也可以不加这个，由下面的循环控制退出
        }

        for(int i=0;i<nums.size();i++)
        {
            if(used[i]==1) continue;
            
            if(i>0 && nums[i]==nums[i-1] && used[i-1]==0) continue;
            //这里写成if(i>0 && nums[i]==nums[i-1]) continue;是不正确的，会考虑不全。

            path.push_back(nums[i]);
            used[i]=1;
           
            backtracing(nums);

            path.pop_back();
            used[i]=0;
        }

    }
};